初中数学北师大版八年级下册2 直角三角形优质课件ppt

这是一份初中数学北师大版八年级下册2 直角三角形优质课件ppt，共39页。PPT课件主要包含了是直角三角形，勾股定理与逆定理，勾股定理，即a2+b2c2，方法一，方法二，∴a2+b2c2，a+b2，c2+，方法三等内容，欢迎下载使用。

（2）直角三角形的定义是什么？
（3）三角形内角和的性质是什么？
有一个是直角的三角形叫直角三角形.
三角形内角和等于180°.
思考：（1）三角形的分类？
锐角三角形，直角三角形，钝角三角形.
直角三角形的两个锐角互余.
这节课我们一起来证明直角三角形的判定与性质.
（4） 前面我们探究过直角三角形的哪些性质？
在直角三角形中，如果一个锐角等于30°，那么它所对的直角边等于斜边的一半.
在直角三角形中，如果一条直角边等于斜边的一半，那么这条直角边所对的锐角等于30°.
1.复习直角三角形的相关知识，归纳并掌握直角三角形的性质和判定.
2.学习并掌握勾股定理及其逆定理，能够运用其解决问题.
3.结合具体事例理解互逆命题、互逆定理的概念,并体会原命题成立时，其逆命题不一定成立.
直角三角形的性质与判定
（1）直角三角形的两个锐角有怎样的关系？
根据三角形的内角和定理，即可得到“直角三角形的两锐角互余”.
（2）如果一个三角形中有两个角互余，那么这个三角形是直角三角形吗？
已知：如图，在△ABC中， ∠A +∠B=90°.求证： △ABC是直角三角形.
在△ABC中，∵ ∠A +∠B +∠C=180°， 又∠A +∠B=90°，∴∠C=90°，∴△ABC是直角三角形.
如果一个三角形中有两个角互余，那么这个三角形是直角三角形.
性质定理 直角三角形的两锐角互余.
判定定理 有两个角互余的三角形是直角三角形.
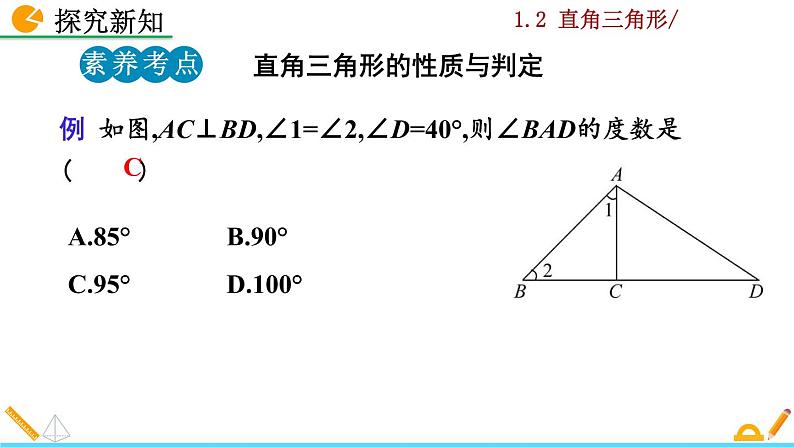
例 如图,AC⊥BD,∠1=∠2,∠D=40°,则∠BAD的度数是 (　 　)
A.85°B.90°C.95°D.100°
直角三角形中,一个锐角等于另一个锐角的2倍,则较小的锐角是_________.
直角三角形两条直角边的平方和等于斜边的平方.
勾股定理在西方文献中又称为毕达哥拉斯定理.
勾股定理的3种证明方法：
∵ (a+b)2 = c2+ ，
a2+2ab+b2 = c2+2ab，
大正方形的面积可以表示为 ；也可以表示为 ；
∵ c2= +(b-a)2，
c2 =2ab+b2-2ab+a2，
∴ a2+b2=c2.
大正方形的面积可以表示为 ；也可以表示为　　　　 ．
+(b-a)2
我们曾用度量的办法得出这个结论.
勾股定理反过来，怎么叙述呢？
如果一个三角形两边的平方和等于第三边的平方,那么这个三角形是直角三角形．
思考：这个命题是真命题吗？为什么？
勾股定理的逆定理的证明：
已知：如图,在△ABC中,AC2+BC2=AB2.求证:△ABC是直角三角形．分析：构造一个直角三角形与△ABC全等，你能自己写出证明过程吗？
证明：作Rt△DEF,使∠E=90°,DE=AC,FE=BC，则DE2+EF2=DF2(勾股定理)．∵AC2+BC2=AB2(已知), DE=AC,FE=BC(作图),∴AB2=DF2，∴AB=DF，∴△ABC≌△DFE（SSS）．∴∠C=∠E=90°,∴△ABC是直角三角形．
勾股定理 直角三角形两条直角边的平方和等于斜边的平方.
逆定理 如果三角形两边的平方和等于第三边的平方,那么这个三角形是直角三角形．
直角三角形的性质定理:1.直角三角形的两个锐角互余.2.勾股定理：直角三角形两条直角边的平方和等于斜边的平方.
直角三角形的判定定理:1.有两个角互余的三角形是直角三角形2.如果三角形两边的平方和等于第三边的平方, 那么这个三角形是直角三角形.
例 已知△ABC的三边长分别为5、12、13，则△ABC的面积为 (　 　)
A.30 D.不能确定
已知：如图，在△ABC中，∠ACB＝90°，AB＝5cm，BC＝3cm，CD⊥AB于D，求CD的长.
解：∵△ABC是直角三角形，AB＝5cm，BC＝3cm，由勾股定理得AC2＝AB2－BC2，∴AC＝4cm，又S△ABC＝ BC·AC＝ AB·CD， CD＝BC·AC÷AB＝2.4cm，∴CD的长是2.4cm.
定理:如果一个三角形两边的平方和等于第三边的平方,那么这个三角形是直角三角形．
勾股定理:直角三角形两条直角边的平方和等于斜边的平方．
下面两个定理的条件和结论有什么样的关系？
一个命题的条件和结论分别是另一个命题的结论和条件．
上面每组中两个命题的条件和结论也有类似的关系吗?与同伴交流．
上面每两个命题的条件和结论恰好互换了位置．
在两个命题中，如果第一个命题的条件是第二个命题的结论，而第一个命题的结论是第二个命题的条件，那么这两个命题叫做互逆命题.
如果把其中一个命题叫做原命题，那么另一个命题就叫做它的逆命题.
注意：原命题是真命题，而逆命题不一定是真命题!
如果一个定理的逆命题经过证明是真命题，那么它也是一个定理，我们称它们为互逆定理.其中一个定理称为另一个定理的逆定理.
注意：（1）逆命题、互逆命题不一定是真命题，但逆定理、互逆定理，一定是真命题.（2）每个定理都有逆命题，但每个定理不一定有逆定理.
例 指出下列命题的条件和结论，并说出它们的逆命题.
条件：一个三角形是直角三角形.结论：它的两个锐角互余.逆命题：如果一个三角形的两个锐角互余，那么这个三角形是直角三角形.
(1)如果一个三角形是直角三角形，那么它的两个锐角互余.
条件：一个三角形是等边三角形.结论：它的每个角都等于60°.逆命题：如果一个三角形的每个角都等于60°，那么这个三角形是等边三角形.
(2)等边三角形的每个角都等于60°.
条件：两个三角形是全等三角形.结论：它们的对应角相等.逆命题：如果两个三角形的对应角相等，那么这两个三角形全等.
(3)全等三角形的对应角相等.
下列命题:①直角三角形两条直角边的平方和等于斜边的平方;②若a>b,则ac2>bc2;③全等三角形对应角相等;④直角三角形两锐角互余.其中原命题与逆命题均为真命题的是(　 　)
A.①②④B.①④C.③④ D.④
（2020·荆门）△ABC中，AB=AC，∠BAC=120°，BC= ，D为BC的中点，AE= AB，则△EBD的面积为（ ）
A. B.C. D.
1. 在一个直角三角形中,有一个锐角等于35°,则另一个锐角的度数是(　 　)A.75° B.65°C.55° D.45°
2. 如图是一张直角三角形的纸片，两直角边AC＝6 cm，BC＝8 cm，现将△ABC折叠，使点B与点A重合，折痕为DE，则BE的长为（ ）A.4 cm B.5 cm C.6 cm D.10 cm
3. 下列长度的三条线段能组成直角三角形的是 (　 　)A.3,4,5B.2,3,4C.4,6,7D.5,11,12
4.三角形的三边长a,b,c满足2ab=(a+b)2-c2,则此三角形的形状是_________三角形.
5.“直角都相等”与“相等的角是直角”是 (　 　)A.互为逆命题 B.互逆定理　C.公理 D.假命题
1、如图，△ABC中，AB＝AC，∠BAC＝90°，D是BC上任一点.求证：BD2＋CD2＝2AD2.
过点A作AE⊥BC于E，则在Rt△ADE中，AD2＝DE2＋AE2，又∵AB＝AC，∠BAC＝90°，∴AE＝BE＝CE，∵BD2＋CD2＝（BE－DE）2＋（CE＋DE）2＝BE2＋CE2＋2DE2＝2AE2＋2DE2＝2AD2，即BD2＋CD2＝2AD2.
2、如图,直角三角形ABC中,∠ACB=90°,AC=12cm,BC=5cm,AB=13 cm,过点C作CD⊥AB于点D.
解:(1)∵CD⊥AB(已知),∴∠CDA=90°,∴∠A+∠1=90°,∵∠1+∠2=90°,∴∠A=∠2.同理可得,∠1=∠B.
(1)找出图中相等的锐角,并说明理由.
解:(2)点A到直线BC的距离为12 cm.点C到直线AB的距离为线段CD的长度.S△ABC= AC×BC= AB×CD.∵AC=12 cm，BC=5 cm，AB=13 cm,代入上式,解得CD= cm.
(2)求出点A到直线BC的距离以及点C到直线AB的距离.
如图,在四边形ABCD中,∠B=90°,AB=BC=2,AD=1,CD=3.求四边形ABCD的面积.
解：连接AC,∵∠B=90°,AB=BC=2,∴AC=2 ,∵AD=1,CD=3,∴AD2+AC2=12+(2 )2=9,CD2=9,
∴AD2+AC2=CD2,∴△ADC是直角三角形,∴∠DAC=90°,在Rt△ABC中,S△ABC= BC·AB= ×2×2=2,在Rt△ADC中,S△ADC= AD·AC= ×1×2 = ,∴S四边形ABCD=S△ABC+S△ADC=2+ .