数学八年级下册3 线段的垂直平分线优质课课件ppt

这是一份数学八年级下册3 线段的垂直平分线优质课课件ppt，共30页。PPT课件主要包含了画一画，做一做，结论证明，几何语言，连接ABAC，90°-2α等内容，欢迎下载使用。

1.回顾一下线段的垂直平分线的性质定理和判定定理.2.线段的垂直平分线的作法.
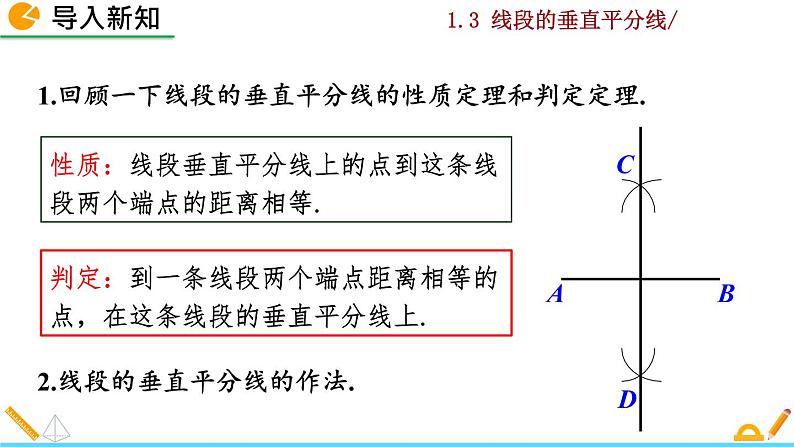
性质：线段垂直平分线上的点到这条线段两个端点的距离相等.
判定：到一条线段两个端点距离相等的点，在这条线段的垂直平分线上.
1. 理解并掌握三角形三边的垂直平分线的性质.
2. 能够运用三角形三边的垂直平分线的性质解决实际问题.
3. 能够利用尺规作已知底边及底边上的高的等腰三角形.
利用尺规作三角形三条边的垂直平分线，完成之后你发现了什么？
发现：三角形三边的垂直平分线交于一点．这一点到三角形三个顶点的距离相等．
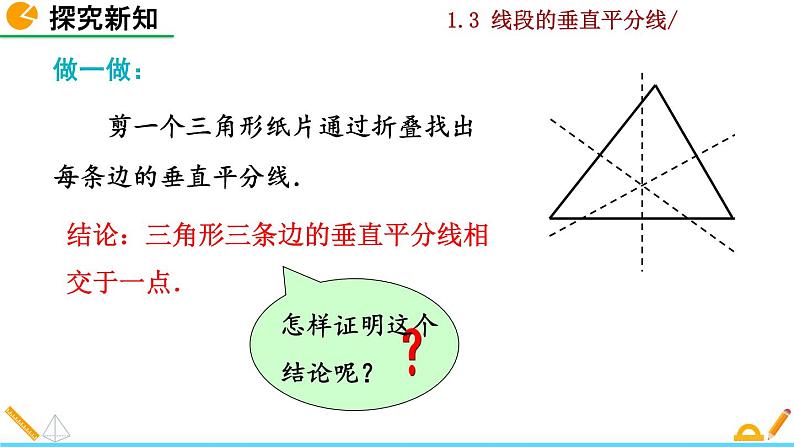
剪一个三角形纸片通过折叠找出每条边的垂直平分线．
结论：三角形三条边的垂直平分线相交于一点．
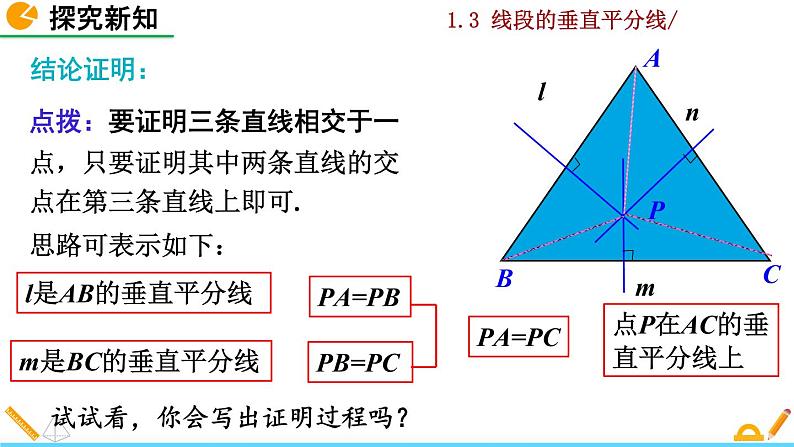
点拨：要证明三条直线相交于一点，只要证明其中两条直线的交点在第三条直线上即可.思路可表示如下：
试试看，你会写出证明过程吗？
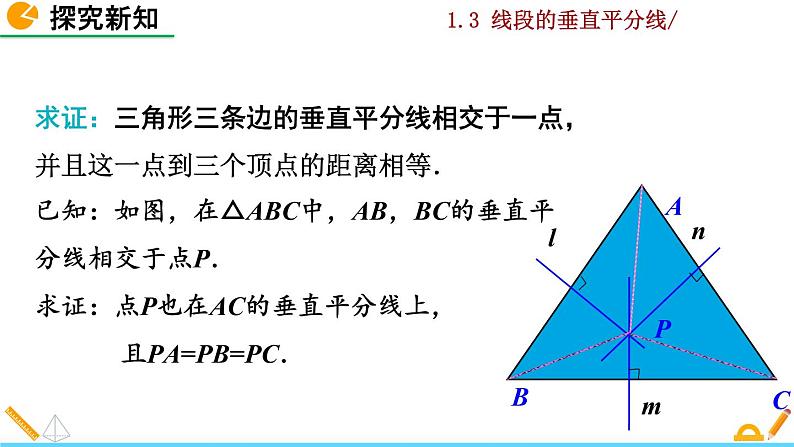
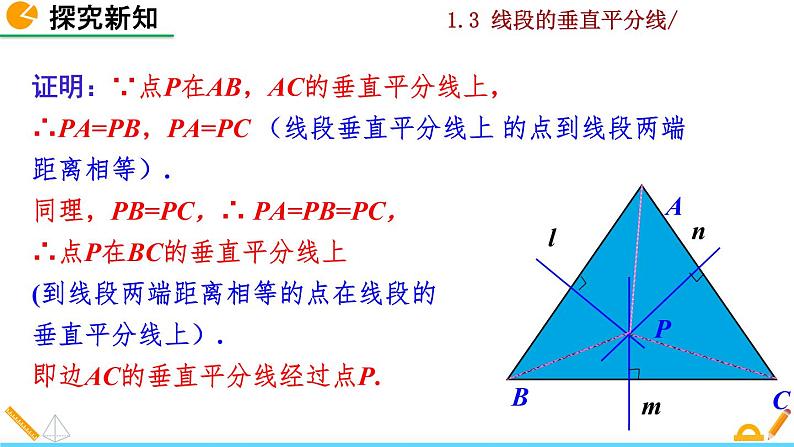
求证：三角形三条边的垂直平分线相交于一点，并且这一点到三个顶点的距离相等．已知：如图，在△ABC中，AB，BC的垂直平分线相交于点P． 求证：点P也在AC的垂直平分线上， 且PA=PB=PC．
证明：∵点P在AB，AC的垂直平分线上， ∴PA=PB，PA=PC （线段垂直平分线上 的点到线段两端距离相等）.同理，PB=PC，∴ PA=PB=PC，∴点P在BC的垂直平分线上 (到线段两端距离相等的点在线段的垂直平分线上）.即边AC的垂直平分线经过点P.
文字语言： 三角形三条边的垂直平分线相交于一点,并且这一点到三个顶点的距离相等.
∵点P 为△ABC 三边垂直平分线的交点，∴PA =PB=PC．
分别作出锐角三角形、直角三角形、钝角三角形三边的垂直平分线，说明交点分别在什么位置.
锐角三角形三边的垂直平分线交点在三角形内；直角三角形三边的垂直平分线交点在斜边上；钝角三角形三边的垂直平分线交点在三角形外.
（1）已知三角形的一条边及这条边上的高，你能作出三角形吗?如果能，能作几个?所作出的三角形都全等吗?
已知：三角形的一条边a和这边上的高h.求作：△ABC，使BC=a，BC边上的高为h.
能作出无数个这样的三角形，它们并不全等.
（2）已知等腰三角形的底边，你能用尺规作出等腰三角形吗?如果能，能作几个?所作出的三角形都全等吗?
这样的等腰三角形有无数多个.根据线段垂直平分线上的点到线段两个端点的距离相等，只要作底边的垂直平分线，取它上面除底边的中点外的任意一点，和底边的两个端点相连接，都可以得到一个等腰三角形．如图所示，这些三角形不都全等．
（3）已知等腰三角形的底及底边上的高,你能用尺规作出等腰三角形吗？能作几个？
这样的等腰三角形只有两个，并且它们是全等的，分别位于已知底边的两侧．
已知一个等腰三角形的底及底边上的高,求作这个等腰三角形.
已知：线段a，h.求作：△ABC，使AB=AC，BC=a，高AD=h.
作法：1．作BC=a；
2．作线段BC的垂直平分线MN交BC于D点；
3．以D为圆心，h长为半径作弧交MN于A点；
△ABC就是所求作的三角形.
已知：直线 l 和 l 上一点P．求作：PC⊥ l ．
作法：①以点P为圆心，以任意长为半径作弧，与直线 l 相交于点A和B．②作线段AB的垂直平分线PC．直线PC就是所求 l 的垂线．
已知直线l和l上一点P，利用尺规作 l 的垂线，使它经过点P.
已知直线 l 和线外一点P，利用尺规作 l 的垂线，使它经过点P.
①先以点P为圆心，大于点P到直线 l 的垂直距离R为半径作圆，交直线 l 于点A，B.②分别以A、B为圆心，大于线段AB长度的一半为半径作圆，相交于C、D两点.③过两交点作直线 l ',此直线为l 过点P的垂线.
（2020·宜昌）如图，点E，F，G，Q，H在一条直线上，且EF=GH，我们知道按如图所作的直线l为线段FG的垂直平分线.下列说法正确的是（ ）
A. l是线段EH的垂直平分线B. l是线段EQ的垂直平分线C. l是线段FH的垂直平分线D. EH是l的垂直平分线
1. 如图,等腰△ABC中，AB=AC，∠A=20°．线段AB的垂直平分线交AB于D，交AC于E，连接BE，则∠CBE等于（ ）A．80° 　　B．70° C．60° D．50°
2. 已知:如图,在△ABC中,边AB,BC的垂直平分线交于点P.则下列结论一定成立的个数为(　 　)①PA=PB=PC.②点P在AC的垂直平分线上.③∠BPC=90°+ ∠BAC.④∠BAP=∠CAP.A.1个B.2个C.3个D.4个
3. 如图,有A,B,C三个居民小区,现决定在三个小区之间修建一个购物超市,使超市到三个小区的距离相等,则超市应建在 (　 　)A.AC,BC两边高线的交点处　B.AC,BC两边垂直平分线的交点处　C.AC,BC两边中线的交点处　D.∠A,∠B两内角平分线的交点处
4.如图,在△ABC中,点D是边AB,BC的垂直平分线交点,连接AD并延长交BC于点E,若∠AEC=3∠BAE=3α,则∠CAE=____________(用含α的式子表示). 
1.如图,在△ABC中,点D为BC上一点,连接AD,点E在线段AD上,并且∠1=∠2,∠3=∠4,求证:AD垂直平分BC.
证明:∵∠1=∠2,∠3=∠4,∴EB=EC,且∠1+∠3=∠2+∠4,即∠ABC=∠ACB,∴AB=AC,∴A与E都在线段BC的垂直平分线上,则AD垂直平分BC.
2.如图,在△ABC中，D为BC的中点，E、F分别是AB、AC上的点，且DE⊥DF.求证：BE＋CF＞EF.
证明:延长FD到G，使DG＝DF.连接EG、BG.在△CDF和△BDG中，CD＝BD,∠CDF＝∠BDG,DF＝DG，∴△CDF≌△BDG（SAS），∴BG＝CF.∵DE⊥DF，DF＝DG，∴EG＝EF.在△BEG中，BE＋BG＞EG，∴BE＋CF＞EF.
如图,在△ABC中,AC边的垂直平分线DM交AC于点D,BC边的垂直平分线EN交BC于点E,DM与EN相交于点F .
解：∵DM是AC边的垂直平分线,∴MA=MC,∵EN是BC边的垂直平分线,∴NB=NC,AB=AM+MN+NB=MC+MN+NC=△CMN的周长=20 cm.
(1)若△CMN的周长为20 cm,求AB的长.
解：∵MD⊥AC,NE⊥BC,∴∠ACB=180°-∠MFN=110°,∴∠A+∠B=70°,∵MA=MC,NB=NC,∴∠MCA=∠A,∠NCB=∠B,∴∠MCN=40°.
(2)若∠MFN=70°,求∠MCN的度数.