初中数学北师大版七年级下册2 幂的乘方与积的乘方精品ppt课件

这是一份初中数学北师大版七年级下册2 幂的乘方与积的乘方精品ppt课件，文件包含课时1幂的乘方pptx、课时1幂的乘方doc等2份课件配套教学资源，其中PPT共19页， 欢迎下载使用。

1.了解幂的乘方的运算法则，熟练运用幂的乘方的运算法则进行实际计算.（重点） 2.掌握幂的乘方的运算法则的推导.（难点） 3.体会数式通性和从具体到抽象的思想方法在研究数学问题中的作用.
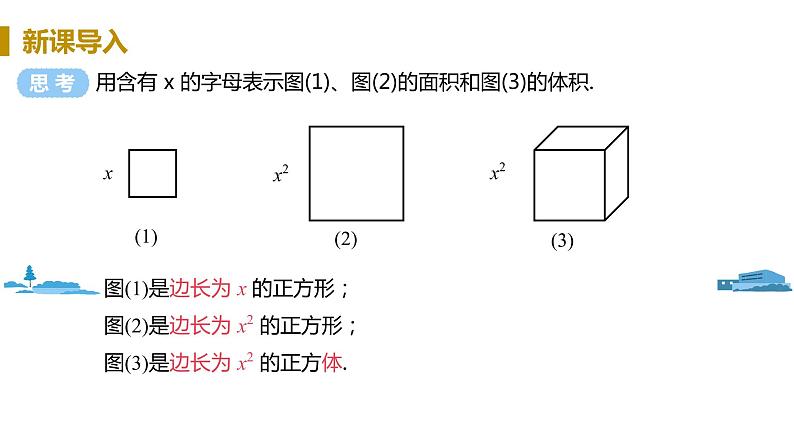
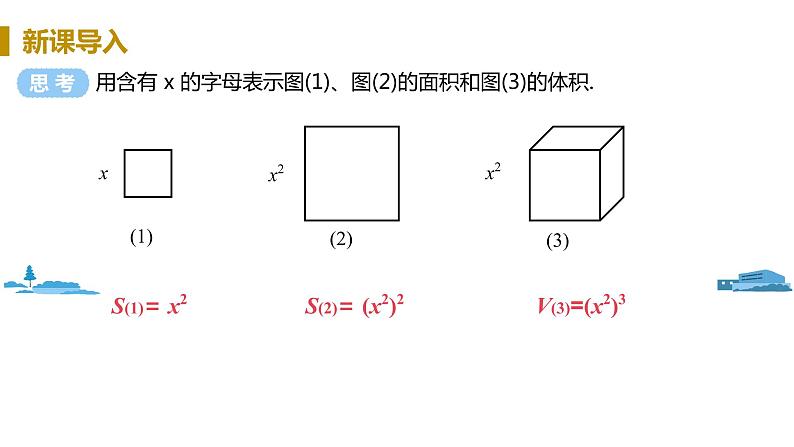
用含有 x 的字母表示图(1)、图(2)的面积和图(3)的体积.
图(1)是边长为 x 的正方形；图(2)是边长为 x2 的正方形；图(3)是边长为 x2 的正方体.
S(1)= x2
S(2)= (x2)2
V(3)=(x2)3
(1) (x2)2 = x2∙2= x4 ;(2) (x2)3 = x2∙3= x6 .
观察计算结果，你能发现什么规律？(1) (x2)2 = x2∙x2 = x2+2= x4 ; (2) (x2)3 = x2∙x2∙x2 = x2+2+2= x6 .
观察计算结果，你能发现什么规律？（m，n为正整数）(1) (32)3=32×32×32=36 ;(2) (a2)3=a2×a2×a2=a6 ;(3) (am)3=am×am×am=a3m （m是正整数）;(4) (am)n=am×am×∙∙∙am=amn （m，n为正整数）.
以上4个式子都是幂的乘方的形式，根据已经学过的乘方的意义和同底数幂的乘法性质可以得出幂的乘方的结果中底数不变，指数为两个指数的乘积（其中指数均为正整数）.
知识点1 幂的乘方
符号表示：(am)n=amn（m，n都是正整数）.
一般地，对于任意底数a与任意正整数m，n. (am)n=am×am×∙∙∙am=amn =a(m+m+m+∙∙∙+m)
知识点1 幂的乘方
示例： = = = =
(1) 幂的乘方的性质也可以推广为 [(am)n]p=amnp(m，n，p都为正整数).(2) 幂的乘方的性质可以逆用，即 amn=(am)n (m，n为正整数).
(1)在形式上，幂的乘方的底数本身就是一个幂，根据乘方的意义和同底数幂的乘法的性质可以推出幂的乘方的性质；(2)在幂的乘方中，底数可以是单项式，也可以是多项式.
计算下列式子：(1) (103)5 ; (2) (a4)4 ; (3) (am)2 ; (4) -(x4)3 .
解：(1) (103)5=103×5=1015 ;
(2) (a4)4 =a4×4=a16 ;
(3) (am)2 = am×2= a2m ;
(4) -(x4)3=-x4×3=-x12 .
(3) -[(a-b)3 ]4 = -(a-b)3×4= -(a-b)12 .
计算：(1) (an+1)2 ; (2) [(-x)7]4 ; (3) -[(a-b)3 ]4 .
解：(1) (an+1)2 = a(n+1)×2 = a2n+2 ;
(2) [(-x)7]4 = (-x)7×4 = (-x)28= x28 ;
已知 a2n=3，求 a4n-a6n 的值.
解：a4n-a6n = (a2n)2- (a2n)3 = 32-33 = -18 .
1.计算(x3)3的结果是（ ）A. x5B. x6C. x8D. x9
2. 下列运算正确的是（ ）A. a2·a3=a6 B. (a2)3=a6C. a5·a5=a25D. (3x)3=3x3
3. （1）若2x+y=3，则4x·2y= . （2）已知3m·9m·27m·81m=330，求m的值.
解：3m·32m·33m·34m=330 310m=330 m=3
已知16m=4×22n-2，27n=9×3m+3 ，求 m，n 的值.