初中数学北师大版七年级下册2 幂的乘方与积的乘方精品课件ppt

这是一份初中数学北师大版七年级下册2 幂的乘方与积的乘方精品课件ppt，文件包含课时2积的乘方pptx、课时2积的乘方doc等2份课件配套教学资源，其中PPT共19页， 欢迎下载使用。
1.了解并掌握积的乘方的法则，熟练运用幂的乘方的运算法则进行实际计算.（重点） 2.掌握积的乘方的运算法则的推导.（难点） 3.体会数式通性和从具体到抽象的思想方法在研究数学问题中的作用.
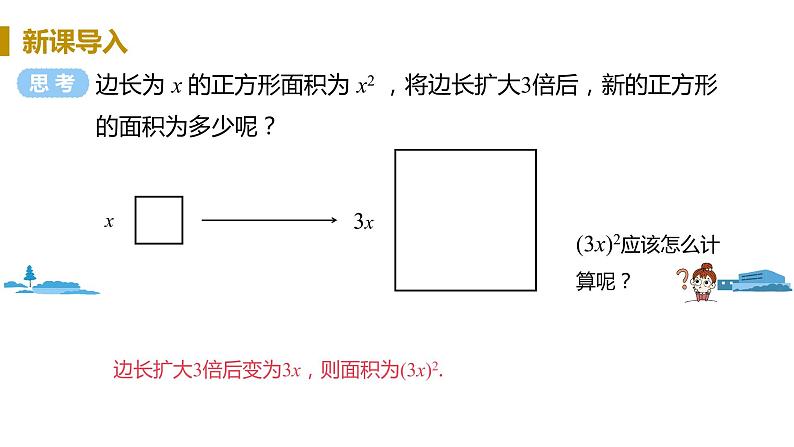
边长为 x 的正方形面积为 x2 ，将边长扩大3倍后，新的正方形的面积为多少呢？
边长扩大3倍后变为3x，则面积为(3x)2.
观察计算结果，你能发现什么规律？(1) (3x)2=3x·3x=(3·3)(x·x)=32x2=9x2 ; (2) (ab)3=ab·ab·ab=(a·a·a)(b·b·b)=a3·b3=a3b3 .
以上2个式子都是积的乘方的形式，根据已经学过的乘方的意义、同底数幂的乘法运算以及幂的乘方运算法则可以得出积的乘方计算，把积的每一个因式分别乘方，再把所得的幂相乘（其中指数均为正整数）.
知识点1 积的乘方
一般地，对于任意底数a，b与任意正整数 n.
符号表示：(ab)n=anbn（n为正整数）.
(1)在积的乘方中，底数中的a，b可以是单项式，也可以是多项式；(2)在进行积的乘方的运算时，要把底数中的每个因式分别乘方，不要漏掉任何一项.
(1) 积的乘方的性质也适用于三个及三个以上因式的积的乘方(abc)n=anbncn（n为正整数）.
(2) 积的乘方的性质可以逆用，即anbn=(ab)n（n为正整数）.
(1)当底数中含有“-”时，应将其视为“-1”，作为一个因式，防漏乘；(2)在积的乘方中，底数是乘积的形式，要避免出现(a+b)n=an+bn.
示例：
a
b
an
bn
计算下列式子：(1) (2a)3 ; (2) (-5b)3 ; (3) (xy2)2 ; (4) (-2x3)4 .
解：(1) (2a)3 =23·a3=8a3 ;
(2) (-5b)3 =(-5)3·b3=-125b3 ;
(3) (xy2)2 =x2·(y2)2=x2y4 ;
(4) (-2x3)4 =(-2)4·(x3)4=16x12 .
解：(1) (-3×102)3 =(-3)3×(102)3=-27×106=-2.7×107 ;
(3) (-a2b3)3 =(-1)3·(a2)3·(b3)3=-a6b9 .
计算： .
意义：积的乘方是指底数是乘积形式的乘方.
① (-2x2)3；② (-2ab2)3；③ (xy2)2；④ 48×0.258
填空：① a3·b3=( )3；② (-2)4a4=( )4；
3. 计算：0.1252015×82016
解：原式=0.1252015×82015×8 =（0.125×8）2015×8 =12015×8 =8
下列运算正确的是（ ）A. m2+2m3=3m5 B. m2·m3=m6 C. (-m)3=-m3 C. (mn)3=mn3
分析：选项A中，m2和2m3不是同类项，不能合并，故而错误；选项B中，m2·m3=m5，故而错误；选项D中，(mn)3=m3n3，故而错误.
若(4am+nbm)3=64a15b9成立，则（ ）A. m=3，n=2 B. m=n=2 C. m=6，n=2 D. m=3，n=5
分析：(4am+nbm)3 =43×(am+n)3×(bm)3 =64a3(m+n)b3m =64a15b9 .则3(m+n)=15，3m=9，所以m=3，n=2 .