






苏教版 (2019)必修 第二册第13章 立体几何初步13.2 基本图形位置关系公开课ppt课件
展开1.平面(1)平面的概念平静的湖面给我们以平面的形象.和点、直线一样,平面也是从现实世界中抽象出来的几何概念.(2)平面的画法平面通常用平行四边形来表示,当平面水平放置的时候,一般用水平放置的正方形的直观图作为平面的直观图.
(3)平面的表示方法平面通常用希腊字母α,β,γ等表示,也可以用平行四边形的两个相对顶点的字母表示,如平面α、平面AC等.
【思考】平面是否有大小呢?提示:①平面和点、直线一样,是只描述而不加定义的原始概念,不能进行度量.②平面无厚薄、无大小,是无限延展的.
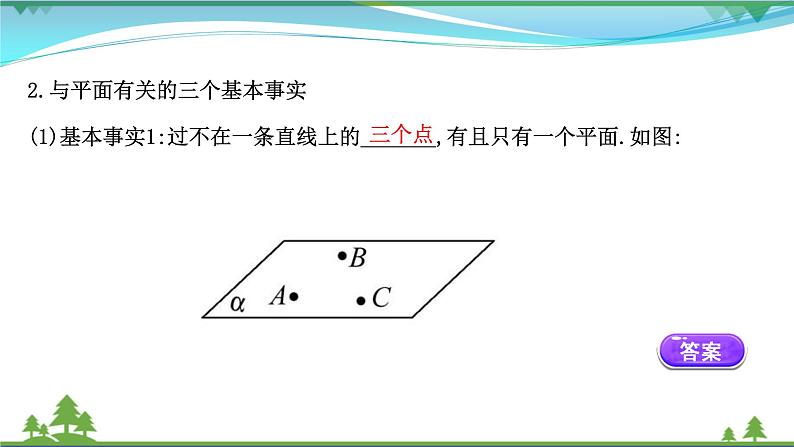
2.与平面有关的三个基本事实(1)基本事实1:过不在一条直线上的_______,有且只有一个平面.如图:
【思考】 基本事实1有什么意义及作用呢?提示:意义:是在空间确定一个平面位置的方法与途径,而确定平面是将空间问题转化为平面问题的重要条件,这个转化是立体几何中解决相当一部分问题的主要的思想方法.作用:①确定平面;②证明点、线共面.
(2)基本事实2:如果一条直线上的_______在一个平面内,那么这条直线在这个平面内.
空间中点、直线和平面的位置关系,可以借助集合中的符号来表示.例如,在长方体ABCD-A1B1C1D1中:
【思考】 (1)如何从集合的角度理解点、线、面之间的关系呢?提示:①直线可以看成无数个点组成的集合,故点与直线的关系是元素与集合的关系,用“∈”或“∉”表示.②平面也可以看成点集,故点与平面的关系也是元素与集合的关系,用“∈”或“∉”表示.③直线与平面都是点集,它们之间的关系可看成集合与集合的关系,故用“⊂”或“⊄”表示.这样,基本事实2就可以用符号表示为 ⇒AB⊂α.
(2)基本事实2有什么意义及作用呢?提示:意义:说明了平面与曲面的本质区别.通过直线的“直”来刻画平面的“平”,通过直线的“无限延伸”来描述平面的“无限延展”.作用:既是判断直线是否在平面内的依据,又是检验平面的方法.
(3)基本事实3:如果两个不重合的平面有一个_______,那么它们有且只有一条过该点的公共直线.这样,基本事实3就可以用符号表示为 ⇒α∩β=l且P∈l.
【思考】基本事实3有什么意义及作用呢?提示:意义:揭示了两个平面相交的主要特征,提供了确定两个平面交线的方法.作用:①判断两个平面是否相交;②确定两个平面的交线;③证明若干点共线问题.
3.平面性质的三个基本事实的三个推论推论1:经过一条直线和这条直线外的一点,有且只有一个平面.
推论2:经过两条相交直线,有且只有一个平面.
推论3:经过两条平行直线,有且只有一个平面.
【基础小测】 1.辨析记忆(对的打“√”,错的打“×”)(1)一个平面的面积是16 cm2.( )(2)直线l与平面α有且只有两个公共点.( )(3)四条线段首尾相连一定构成一个平面四边形.( )(4)8个平面重叠起来要比6个平面重叠起来厚.( )(5)空间不同三点确定一个平面.( )
提示:(1)×.平面是没有大小的.(2)×.一条直线和一个平面公共点的个数可能为0个,1个或无数个,不可能只有2个公共点.(3)×.也可能是四条边不在同一个平面内的空间四边形.(4)×.平面是没有大小、厚度之分的.(5)×.只有不共线的三点可以确定一个平面.
2.若一直线a在平面α内,则正确的图形是( )
【解析】选A.选项B,C,D中直线a在平面α外,选项A中直线a在平面α内.
3.(教材二次开发:习题改编)如图所示,下列符号表示错误的是( ) A.l∈αB.P∉lC.l⊂αD.P∈α【解析】选A.观察图知:P∉l,P∈α,l⊂α,则l∈α是错误的.
类型一 图形、文字、符号语言的相互转化(数学抽象、直观想象)【题组训练】1.如图所示,用符号语言表示以下图形中点、直线、平面之间的位置关系:①点A,B在直线a上________; ②直线a在平面α内________; ③点D在直线b上,点C在平面α内________.
2.将下面用符号语言表示的关系用文字语言予以叙述,并用图形语言予以表示.α∩β=l,A∈l,AB⊂α,AC⊂β.3.根据下列条件画出图形:平面α∩平面β=直线AB,直线a⊂α,直线b⊂β,a∥AB,b∥AB.
【解析】1.根据点、线、面位置关系及其表示方法可知:①A∈a,B∈a,②a⊂α,③D∈b,C∈α.答案:①A∈a,B∈a ②a⊂α ③D∈b,C∈α2.文字语言叙述为:点A在平面α与平面β的交线l上,直线AB,AC分别在平面α,β内,图形语言表示如图所示.
【解题策略】(1)用文字语言、符号语言表示一个图形时,首先仔细观察图形有几个平面、几条直线且相互之间的位置关系如何,试着用文字语言表示,再用符号语言表示.(2)根据符号语言或文字语言画相应的图形时,要注意实线和虚线的区别.
【补偿训练】用符号语言表示下列语句,并画出图形:(1)三个平面α,β,γ相交于一点P,且平面α与平面β相交于PA,平面α与平面γ相交于PB,平面β与平面γ相交于PC;(2)平面ABD与平面BDC相交于BD,平面ABC与平面ADC相交于AC.
【解析】(1)符号语言表示:α∩β∩γ=P,α∩β=PA,α∩γ=PB,β∩γ=PC,图形表示:如图①.(2)符号语言表示:平面ABD∩平面BDC=BD,平面ABC∩平面ADC=AC,图形表示:如图②.
类型二 点、线共面问题(直观想象、逻辑推理)【典例】如图,已知:a⊂α,b⊂α,a∩b=A,P∈b,PQ∥a,求证:PQ⊂α.
【解题策略】证明点、线共面问题的常用方法(1)先由部分点、线确定一个面,再证其余的点、线都在这个平面内,即用“纳入法”;(2)先由其中一部分点、线确定一个平面α,其余点、线确定另一个平面β,再证平面α与β重合,即用“同一法”;(3)假设不共面,结合题设推出矛盾,即用“反证法”.
【跟踪训练】 证明两两相交且不共点的三条直线在同一平面内.
【证明】方法一:(纳入法)因为l1∩l2=A,所以l1和l2确定一个平面α.因为l2∩l3=B,所以B∈l2.又因为l2⊂α,所以B∈α.同理可证C∈α.又因为B∈l3,C∈l3,所以l3⊂α.所以直线l1,l2,l3在同一平面内.
方法二:(同一法)因为l1∩l2=A,所以l1,l2确定一个平面α.因为l2∩l3=B,所以l2,l3确定一个平面β.因为A∈l2,l2⊂α,所以A∈α.因为A∈l2,l2⊂β,所以A∈β.同理可证B∈α,B∈β,C∈α,C∈β.所以不共线的三个点A,B,C既在平面α内,又在平面β内.所以平面α和β重合,即直线l1,l2,l3在同一平面内.
【拓展延伸】平面在生活中的应用平面在生活中有着广泛的应用,比如桌子放不稳,想检测是桌子的问题还是地面的问题,我们可以用两根细绳沿桌子四条腿的对角拉直,如果这两根细绳相交,说明桌子四条腿的底端在同一个平面内,说明地面不平,反之说明桌子有问题.
【拓展训练】1.下列各图均是正六棱柱,P,Q,R,S分别是所在棱的中点,这四个点不共面的图形是( )
【解析】选D.在选项A,B,C中,由棱柱、正六边形、中位线的性质,知均有PS∥QR,即在此三个图形中P,Q,R,S共面.
2.如图所示,今有一正方体木料ABCD-A1B1C1D1,其中M,N分别是AB,CB的中点,要过D1,M,N三点将木料锯开,请你帮助木工师傅想办法,怎样画线才能顺利完成?
【解析】作法如下:(1)连接MN并延长交DC的延长线于F,连接D1F交CC1于Q,连接QN;(2)延长NM交DA的延长线于E,连接D1E交AA1于P,连接MP;(3)依次在正方体各个面上画线D1P,PM,MN,NQ,QD1,即为木工师傅所要画的线.
类型三 点共线、线共点、面共线问题(直观想象、逻辑推理)角度1 线共点与点共线问题 【典例】如图所示,在正方体ABCD-A1B1C1D1中,E,F分别为AB,AA1的中点.求证:CE,D1F,DA三线交于一点.
【思路导引】证明三线共点,可以先证明两条直线相交,而交点在第三条直线上.
【证明】连接EF,D1C,A1B,因为E为AB的中点,F为AA1的中点,所以EF= A1B,EF∥ A1B,又因为A1B=D1C,A1B∥D1C,所以EF= D1C,EF∥ D1C,所以E,F,D1,C四点共面,可设D1F∩CE=P.
又D1F⊂平面A1D1DA,CE⊂平面ABCD,所以点P为平面A1D1DA与平面ABCD的公共点.又因为平面A1D1DA∩平面ABCD=DA,所以据基本事实3可得P∈DA,即CE,D1F,DA三线交于一点.
【变式探究】本例的条件“E,F分别为AB,AA1的中点,”改为“E,F分别为AB,AA1上的点,且D1F∩CE=M,”求证:点D,A,M三点共线.证明:因为D1F∩CE=M,且D1F⊂平面A1D1DA,所以M∈平面A1D1DA,同理M∈平面BCDA,从而M在两个平面的交线上,因为平面A1D1DA∩平面BCDA=AD,所以M∈AD成立.所以点D,A,M三点共线.
角度2 面共线问题 【典例】在正方体ABCD-A1B1C1D1中,E,F分别是CC1和AA1的中点,画出平面BED1F与平面ABCD的交线并说明理由.【思路导引】找两个平面的交线,需要找到同时在两个平面内的点.
【解析】如图,在平面AA1D1D内,延长D1F,因为D1F与DA不平行,因此D1F与DA必相交于一点,设D1F与DA交于点P,则P∈FD1,P∈AD.又因为D1F⊂平面BED1F,DA⊂平面ABCD,所以P∈平面BED1F,P∈平面ABCD.所以P∈(平面BED1F∩平面ABCD),即P为平面BED1F与平面ABCD的公共点.又B为平面ABCD与平面BED1F的公共点,所以连接PB,PB即为平面ABCD与平面BED1F的交线.
【解题策略】 1.点共线与线共点的证明方法(1)点共线:证明多点共线通常利用基本事实3,即两相交平面交线的惟一性,通过证明点分别在两个平面内,证明点在相交平面的交线上,也可选择其中两点确定一条直线,然后证明其他点也在其上.(2)三线共点:证明三线共点问题可把其中一条作为分别过其余两条直线的两个平面的交线,然后再证两条直线的交点在此直线上,此外还可先将其中一条直线看作某两个平面的交线,证明该交线与另两条直线分别交于两点,再证点重合,从而得到三线共点.
2.确定两平面的交线,关键是确定这两个平面的两个公共点.基本事实3是解决此类问题的主要依据.
【题组训练】1.已知△ABC在平面α外,AB∩α=P,AC∩α=R,BC∩α=Q,如图.求证:P,Q,R三点共线.
【证明】方法一:因为AB∩α=P,所以P∈AB,P∈平面α.又AB⊂平面ABC,所以P∈平面ABC.所以由基本事实3可知:点P在平面ABC与平面α的交线上,同理可证Q,R也在平面ABC与平面α的交线上.所以P,Q,R三点共线.
方法二:因为AP∩AR=A,所以直线AP与直线AR确定平面APR.又因为AB∩α=P,AC∩α=R,所以平面APR∩平面α=PR.因为B∈面APR,C∈面APR,所以BC⊂面APR.又因为Q∈面APR,Q∈α,所以Q∈PR.所以P,Q,R三点共线.
2.如图,已知平面α,β,且α∩β=l.设梯形ABCD中,AD∥BC,且AB⊂α,CD⊂β.求证:AB,CD,l共点(相交于一点).
【证明】因为梯形ABCD中,AD∥BC,所以AB,CD是梯形ABCD的两腰.因为AB,CD必定相交于一点.设AB∩CD=M.又因为AB⊂α,CD⊂β,所以M∈α,M∈β.所以M∈α∩β.又因为α∩β=l,所以M∈l.即AB,CD,l共点(相交于一点).
3.若α∩β=l,A,B∈α,C∈β,试画出平面ABC与平面α,β的交线.
【解析】因为若α∩β=l,A,B∈α,所以AB是平面ABC与α的交线,延长BA交l于D,则D∈平面ABC,因为C∈β,所以CD是平面ABC与β的交线,则对应的图示如图.
【补偿训练】在空间四边形ABCD的边AB,BC,CD,DA上分别取E,F,G,H四点,若EF与HG交于点M,则( )A.M一定在直线AC上B.M一定在直线BD上C.M可能在AC上,也可能在BD上D.M不在AC上,也不在BD上
【解析】选A.由题意得EF⊂平面ABC,HG⊂平面ACD,又EF∩HG=M,故M∈平面ABC,且M∈平面ACD,又平面ABC∩平面ACD=AC,所以M一定在直线AC上.
1.已知直线m⊂平面α,P∉m,Q∈m,则( ) A.P∉α,Q∈αB.P∈α,Q∉αC.P∉α,Q∉αD.Q∈α【解析】选D.因为Q∈m,m⊂α,所以Q∈α. 因为P∉m,所以有可能P∈α,也可能有P∉α.故选D.
2.下列说法中正确的是( )A.三点确定一个平面B.四边形一定是平面图形C.梯形一定是平面图形D.两个不同平面α和β有不在同一条直线上的三个公共点【解析】选C.不共线的三点确定一个平面,故A不正确;四边形有时指空间四边形,故B不正确;梯形的上底和下底平行,可以确定一个平面,故C正确;两个平面如果相交,一定有一条交线,所有这两个平面的公共点都在这条交线上,故D不正确.
3.(教材二次开发:练习改编)已知α,β为平面,A,B,M,N为点,a为直线,下列推理错误的是( )A.A∈a,A∈β,B∈a,B∈β⇒a⊂βB.M∈α,M∈β,N∈α,N∈β⇒α∩β=MNC.A∈α,A∈β⇒α∩β=AD.A,B,M∈α,A,B,M∈β,且A,B,M不共线⇒α,β重合
【解析】选C.因为A∈α,A∈β,所以A∈(α∩β).由基本事实可知α∩β为经过A的一条直线而不是A.故α∩β=A的写法错误.
4.平面α,β相交,α,β内各取两点,这四点都不在交线上,这四点能确定________个平面. 【解析】(1)当四点确定的两条直线平行或相交时,则四个点确定1个平面;(2)当四点确定的两条直线不共面时,这四个点能确定4个平面,如三棱锥的4个顶点.答案:1或4
2021学年13.2 基本图形位置关系课文内容课件ppt: 这是一份2021学年13.2 基本图形位置关系课文内容课件ppt,共53页。PPT课件主要包含了平行四边形,正方形,两个相对顶点的字母,有且只有,两个点,两条相交直线,两条平行直线,三种语言的转换,点线共面问题,共线共点问题等内容,欢迎下载使用。
苏教版必修21.2.1 平面的基本性质说课课件ppt: 这是一份苏教版必修21.2.1 平面的基本性质说课课件ppt,共34页。PPT课件主要包含了平面的画法,图形语言,文字语言,符号语言,公理1的用途,说明图形是存在的,说明图形是唯一的,“有”,“只有一个”,至少有一个等内容,欢迎下载使用。
苏教版 (2019)必修 第二册13.2 基本图形位置关系优质课件ppt: 这是一份苏教版 (2019)必修 第二册13.2 基本图形位置关系优质课件ppt,共34页。PPT课件主要包含了必备知识·自主学习,无数个,有且只有一个,a⊂α,a∩αA,a∥α,此平面内,关键能力·合作学习,课堂检测·素养达标等内容,欢迎下载使用。













