初中数学湘教版八年级下册第3章 图形与坐标综合与测试单元测试课后练习题

期末复习(三)  图形与坐标

考点一  平面直角坐标系内点的坐标

【例1】如图，根据坐标平面内点的位置，写出以下各点的坐标：A，B，C，D，E，F.

【分析】坐标系内点的表示方法应注意：①所在象限，确定符号；②到两坐标轴的距离，确定绝对值的大小.

【解答】根据坐标系中确定点的坐标的方法可知各点的坐标表示如下：

A(-2，3)；B(3，-2)；C(-1，-1)；D(1，1)；E(1，0)；F(0，-3).

【方法归纳】本题考查点的坐标的特征：(1)点到x轴的距离是纵坐标的绝对值，到y轴的距离是横坐标的绝对值；(2)四个象限的符号特点分别是：第一象限(+，+)；第二象限(-，+)；第三象限(-，-)；第四象限(+，-)；(3)x轴上点的纵坐标为0，y轴上点的横坐标为0.

变式练习

1.若a＞0，则点P(-a，2)应在(    )

  A.第一象限内              B.第二象限内         C.第三象限内         D.第四象限内

2.如果点P(m，1-2m)在第四象限，那么m的取值范围是(    )

  A.0＜m＜                B.-＜m＜0            C.m＜0              D.m＞

考点二  建立直角坐标系与利用方位来刻画物体间的相对位置

【例2】如图，这是一所学校的平面示意图，建立适当的平面直角坐标系，并写出教学楼、校门和图书馆的坐标.

【分析】先建立合适的坐标系，再根据坐标系确定教学楼、校门和图书馆的坐标.

【解答】建立如图所示的直角坐标系.根据建立的坐标系可知：教学楼(6，0)，校门(0，0)，图书馆(5，3).本题答案不唯一，坐标系不同，对应的点的坐标不同.

【方法归纳】由已知条件建立合适的直角坐标系的关键是:(1)要正确地确定坐标原点的位置；(2)要准确地确定单位长度.

3.如图是某个小岛的平面示意图，请你建立适当的平面直角坐标系，写出哨所1，哨所2，小广场，雷达，码头，营房的位置.

4.学校在李老师家的南偏东30°方向，距离是500 m，则李老师家在学校的什么位置？画出示意图.

考点三  轴对称的坐标表示

【例3】点(-3，1)关于x轴对称的点坐标为__________，关于y轴对称的点坐标为__________.

【分析】本题主要考查关于x轴、y轴对称点的坐标变化特征，关键是熟练掌握不同的对称情况的点的坐标变化规律.

【解答】根据关于x轴对称点的坐标特点，(-3，1)点关于x轴对称的点坐标为(-3，-1)，关于y轴对称的点坐标为(3，1).

【方法归纳】关于x轴对称点的坐标特点：横坐标不变，纵坐标互为相反数；关于y轴对称点的坐标特点：横坐标互为相反数，纵坐标不变.

5.已知点A的坐标为(-2，3)，点B与点A关于x轴对称，点C与点B关于y轴对称，则点C关于x轴对称的点的坐标为(    )

  A.(-2，3)            B.(2，-3)           C.(2，3)           D.(-2，-3)

考点四  平移的坐标表示

【例4】如果把点A(-1，4)向右平移2个单位长度，再向上平移3个单位长度，那么平移后的坐标是(    )

  A.(1，7)               B.(-1，7)            C.(1，-7)              D.(-1，-7)

【分析】本题直接利用平移中上下左右点的变化规律求解可得.

【解答】A(-1，4)向右平移2个单位长度得到：(-1+2，4)，即：(1，4)，再向上平移3个单位长度得到：(1，4+3)，即(1，7)，故选A.

【方法归纳】本题需要掌握点的平移坐标变化规律：①向右平移a个单位，坐标P(x，y)P(x+a，y)；②向左平移a个单位，坐标P(x，y)P(x-a，y)；③向上平移b个单位，坐标P(x，y)P(x，y+b)；④向下平移b个单位，坐标P(x，y)P(x，y-b).

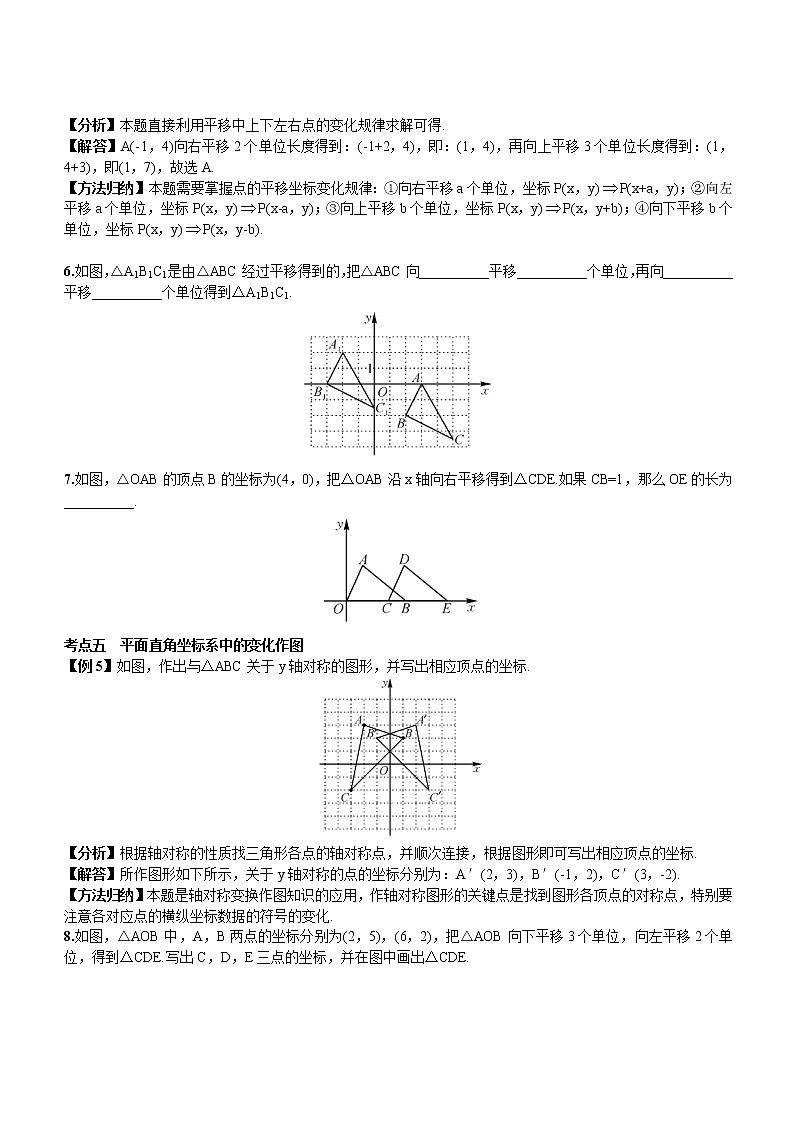
6.如图，△A1B1C1是由△ABC经过平移得到的，把△ABC向__________平移__________个单位，再向__________平移__________个单位得到△A1B1C1.

7.如图，△OAB的顶点B的坐标为(4，0)，把△OAB沿x轴向右平移得到△CDE.如果CB=1，那么OE的长为__________.

考点五  平面直角坐标系中的变化作图

【例5】如图，作出与△ABC关于y轴对称的图形，并写出相应顶点的坐标.

【分析】根据轴对称的性质找三角形各点的轴对称点，并顺次连接，根据图形即可写出相应顶点的坐标.

【解答】所作图形如下所示，关于y轴对称的点的坐标分别为：A′(2，3)，B′(-1，2)，C′(3，-2).

【方法归纳】本题是轴对称变换作图知识的应用，作轴对称图形的关键点是找到图形各顶点的对称点，特别要注意各对应点的横纵坐标数据的符号的变化.

8.如图，△AOB中，A，B两点的坐标分别为(2，5)，(6，2)，把△AOB向下平移3个单位，向左平移2个单位，得到△CDE.写出C，D，E三点的坐标，并在图中画出△CDE.

一、选择题(每小题3分，共30分)

1.已知坐标平面内点A(m，n)在第四象限，那么点B(n，m)在(    )

  A.第一象限            B.第二象限           C.第三象限            D.第四象限

2.在平面直角坐标系中，点P(-3，4)到x轴的距离为(    )

  A.3                   B.-3             C.4                 D.-4

3.下列数据：①4楼9号；②北偏西20°；③金太路3号；④东经108°，北纬30°，不能确定物体位置的是(    )

  A.①③               B.②④              C.②                 D.①③④

4.已知点A，B的坐标分别是(2m+n，2)，(1，n-m).若点A与点B关于y轴对称，则m+2n的值为(    )

  A.-1               B.1                C.0                 D.-3

5.在坐标平面内有一点P(x，y)，若xy=0，那么点P的位置在(    )

  A.原点               B.x轴上              C.y轴上               D.坐标轴上

6.在平面直角坐标系中，已知点A(0，2)，B(-2，0)，C(0，-2)，D(2，0)，则以这四个点为顶点的四边形ABCD是(    )

  A.矩形             B.菱形             C.正方形            D.不能确定

7.已知点P坐标为（2-a,3a+6），且P点到两坐标轴的距离相等，则点P的坐标是(    )

  A.(3，3)          B.(3，-3)           C.(6，-6)                 D.(3，3)或(6，-6)

8.如图，在边长为1的正方形网格中，将△ABC向右平移两个单位长度得到△A′B′C′，则与点B′关于x轴对称的点的坐标是(    )

  A.(0，-1)            B.(1，1)              C.(2，-1)                 D.(1，-2)

9.点P(x,y)在第四象限，且|x|=3,|y|=5，则点P关于x轴对称点的坐标是(    )

  A.(3，-5)               B.(-3，5)               C.(-5，-3)           D.(3，5)

10.把点P(-x，y)变为Q(x，y)，只需(    )

  A.向左平移2x个单位                   B.向右平移2x个单位

  C.作关于x轴对称                      D.作关于y轴对称

二、填空题(每小题3分，共18分)

11.如果点P(x2-4，y+1)是坐标原点，那么2x+y=__________.

12.如图，如果“士”所在位置的坐标为(-2，-2)，相所在位置的坐标为(1，-2)，那么“炮”所在位置的坐标为__________.

13.如图，在直角坐标系中，已知A(-3，-1)、点B(-2,1)，平移线段AB，使点A落在点A1(0，-1)点B落在B1，则点B1的坐标为__________.

14.在平面直角坐标系中，一青蛙从点A(-1，0)处向右跳2个单位长度，再向上跳2个单位长度到点A′处，则点A′的坐标为__________.

15.已知三角形ABC的三个顶点坐标为A(-2，3)，B(-4，-1)，C(2，0).在三角形ABC中有一点P(x，y)经过平移后对应点P1为(x+3，y+5)，将三角形ABC作同样的平移得到三角形A1B1C1，则A1的坐标为__________.

16.如图，在平面直角坐标系中，△PQR是△ABC经过某种变换后得到的图形，观察点A与点P，点B与点Q，点C与点R的坐标之间的关系.在这种变换下，如果△ABC中任意一点M的坐标为(x，y)，那么它们的对应点N的坐标是__________.

三、解答题(共52分)

17.(8分)下图是某市部分地区的示意图，请你建立适当的平面直角坐标系，并写出图中各地点相应的坐标.

18.(8分)如图所示，作字母“M”关于y轴的轴对称图形，并写出所得图形相应各顶点的坐标.

19.(12分)在棋盘中建立如图的直角坐标系，三颗棋子A，O，B的位置如图，它们分别是(-1，1)，(0，0)和(1，0).

  (1)如图2，添加棋子C，使A，O，B，C四颗棋子成为一个轴对称图形，请在图中画出该图形的对称轴；

  (2)在其他格点位置添加一颗棋子P，使A，O，B，P四颗棋子成为一个轴对称图形，请直接写出棋子P的位置的坐标.(写出2个即可)

20.(12分)如图，点A坐标为(-1，1)，将此小船ABCD向左平移2个单位，再向上平移3个单位得A′B′C′D′.

  (1)画出平面直角坐标系；

  (2)画出平移后的小船A′B′C′D′，写出A′，B′，C′，D′各点的坐标.

21.(12分)如图是由边长为1的小正方形组成的方格图.

  (1)请在方格图中建立平面直角坐标系，使点A的坐标为(3,3)，点B的坐标为(-1,0)；

  (2)在x轴上画点C，使△ABC是以AB为腰的等腰三角形，并写出所有满足条件的点C的坐标.(不写作法，保留作图痕迹)

参考答案

变式练习

1.B  2.D

3.图略.以小广场为直角坐标系原点，所在方格线的水平方向为x轴，方格线的竖直方向为y轴建立直角坐标系，并设图中每个小正方形的边长为1.哨所1(0，3)，哨所2(-4，0)，小广场(0，0)，雷达(4，0)，码头(-1，-3)，营房(1，-4).

4.如图所示，李老师家在学校的北偏西30°方向，相距500 m处.

5.C    6.上    2    左    5

7.7

8.图略，由图中易得点C(0，2)，D(-2，-3)，E(4，-1).

复习测试

1.B  2.C  3.C  4.B  5.D  6.B  7.D  8.D  9.D  10.D

11.3或-5    12.(-4,1)    13.(1,1)    14.(1，2)    15.(1，8)    16.(-x，-y)

17.建立坐标系图略：则教育局(-1，3)；苏果超市(0，1)；怡景湾酒店(-3，-2)；同仁医院(3，-3).

18.所作图形略；所得图形相应各顶点的坐标分别为：A′(4，0)，B′(4，3)，C′(2.5，0)，D′(1，3)，E′(1，0).

19.(1)图略，直线l为该图形的对称轴；

  (2)图略，P(0，-1)，P′(-1，-1)都符合题意.

20.(1)所画坐标系图略；

  (2)将各点向左平移2个单位，再向上平移3个单位，顺次连接，如图所示.

结合直角坐标系可得：A′(-3，4)，B′(-2，2)，C′(1，2)，D′(2，3).

21.(1)所作图形略；

  (2)以AB为腰的等腰三角形有：△ABC1，△ABC2，△ABC3，其中点C的坐标分别为：C1(-6,0)，C2(4,0)，C3(7,0).