


人教版九年级下册第二十六章 反比例函数26.1 反比例函数26.1.2 反比例函数的图象和性质优秀ppt课件
展开二次函数y=ax2的图象是什么形状呢?什么确定y=ax2的性质?通常怎样画一个函数的图象?
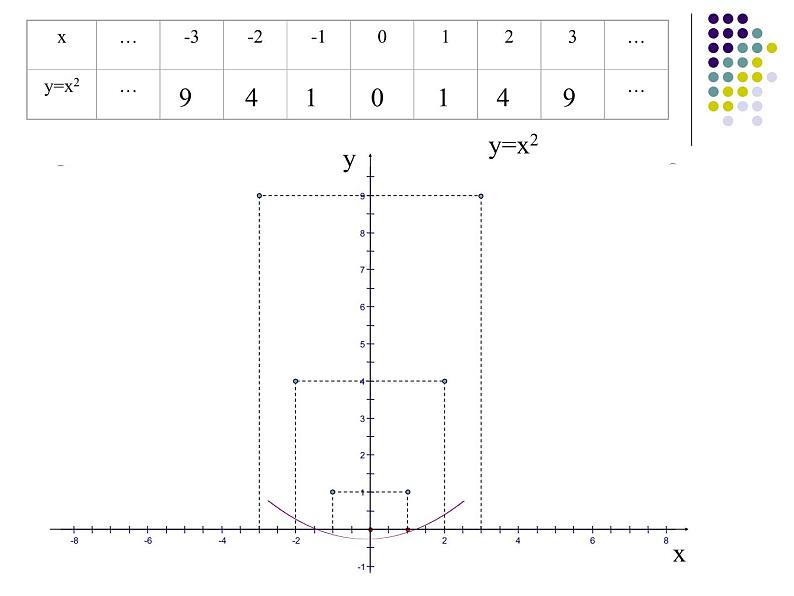
我们来画最简单的二次函数y=x2的图象。
还记得如何用描点法画一个函数的图象吗?
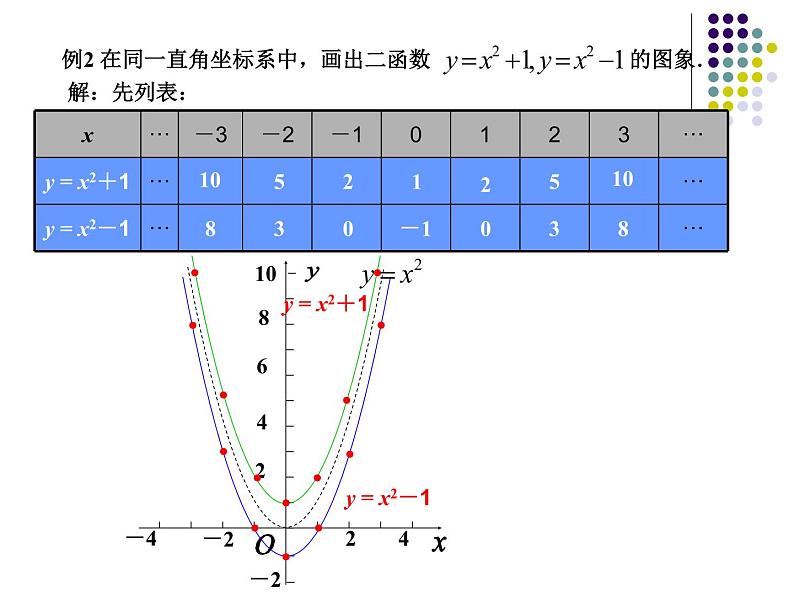
例2 在同一直角坐标系中,画出二函数 的图象.
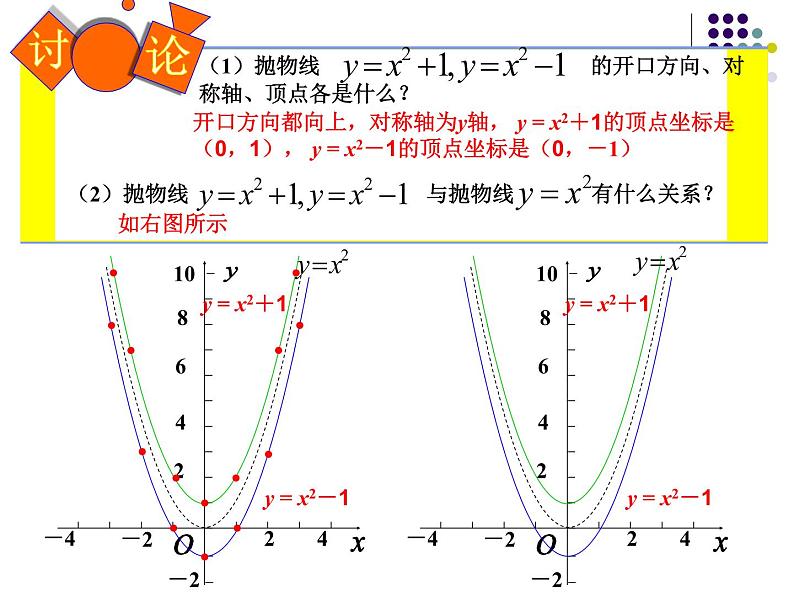
(2)抛物线 与抛物线 有什么关系?
开口方向都向上,对称轴为y轴, y = x2+1的顶点坐标是(0,1), y = x2-1的顶点坐标是(0,-1)
(1)抛物线 的开口方向、对称轴、顶点各是什么?
(1)把抛物线y=x2向上移平移1个单位,就得到抛物线y=x2+1;把抛物线y=x2向下平移1个单位,就得到抛物线y=x2-1。 (2)它们的位置是由+1、-1决定的。
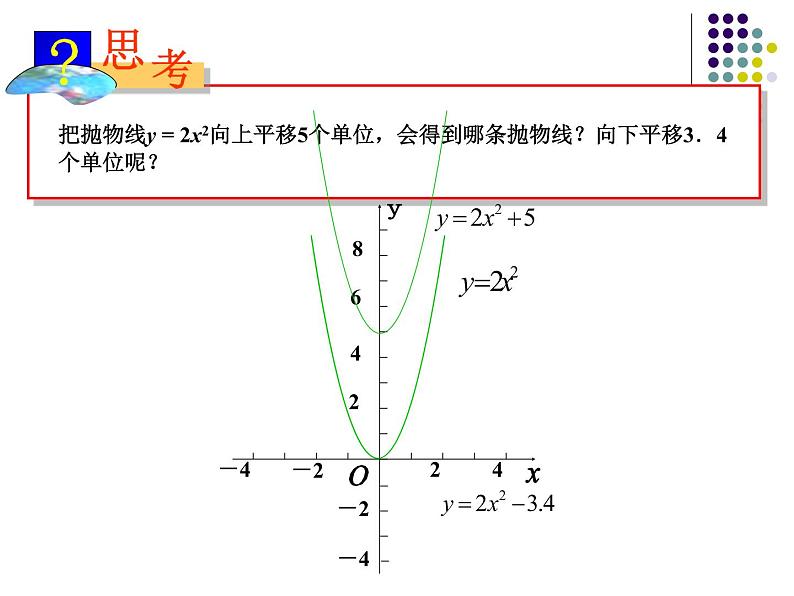
把抛物线y = 2x2向上平移5个单位,会得到哪条抛物线?向下平移3.4个单位呢?
抛物线y = ax2+k的特点:a>0时,开口________, 最 ____ 点是顶点; a<0时,开口________, 最 ____ 点是顶点; 对称轴是 __________________顶点坐标是 __________。
例:在同一个直角坐标系中,画出函数y=-x2和y=-x2+1的图像,并根据图像回答下了问题:
(1)抛物线y=-x2+1经过怎样的平移才能得到抛物线y=-x2
(2)函数y=-x2+1,当x 时, y随x的增大而减小;当x 时,函数y有最大值,最大值y是 其图像与y轴的交点坐标是 ,与x轴的交点坐标是
(3)试说出抛物线y= x2-3的开口方向、对称轴和顶点坐标
一般地抛物线y=ax2+k有如下性质:
二次函数y=ax2+k(a≠0)的图像是一条抛物线,它的对称轴是y轴,顶点坐标是(0,k),是由抛物线y=ax2的图像向上( k>0)或向下( k<0)平移 个单位得到的。
当a>0时,抛物线y=ax2+ k的开口向上, 在对称轴的左边,即x<0时,曲线自左向右下降,函数y随x的增大而减小;在对称轴的右边,即x>0时,曲线自左向右上升,函数y随x的增大而增大。顶点是抛物线的最低点,此时,函数y取得最小值,即当x=0时,y最小值= k
当a<0时,抛物线y=ax2+ k的开口向下, 在对称轴的左边,即x<0时,曲线自左向右上升,函数y随x的增大而增大;在对称轴的右边,即x>0时,曲线自左向右下降,函数y随x的增大而减小。顶点是抛物线的最高点,此时,函数y取得最大值,即当x=0时,y最大值= k
2、课本第十页练习
1、 把抛物线y=2x2向上平移5个单位,会得到哪条抛物线?向下平移3.4个单位呢?
y=x2和y=-x2的图像有什么关系?
1、画抛物线y=ax2+k的图像有几步?
2、抛物线y=ax2+k 中的a决定什么?怎样决定的?k决定什么?它的对称轴是什么?顶点坐标怎样表示?
初中数学人教版九年级下册第二十六章 反比例函数26.1 反比例函数26.1.1 反比例函数精品ppt课件: 这是一份初中数学人教版九年级下册第二十六章 反比例函数26.1 反比例函数26.1.1 反比例函数精品ppt课件,共27页。PPT课件主要包含了一条直线,一条抛物线,自变量x不能为0,①列表,②描点,③连线,y减小,第四象限等内容,欢迎下载使用。
2021学年26.1.2 反比例函数的图象和性质优质ppt课件: 这是一份2021学年26.1.2 反比例函数的图象和性质优质ppt课件,共20页。PPT课件主要包含了学习目标,新课导入,知识点,反比例函数的图象,如何画函数的图象,函数图象画法,描点法,新知探索,当k>0时,当k<0时等内容,欢迎下载使用。
初中数学人教版九年级下册26.1.2 反比例函数的图象和性质优秀ppt课件: 这是一份初中数学人教版九年级下册26.1.2 反比例函数的图象和性质优秀ppt课件,文件包含26122反比例函数的图象和性质的综合运用课件pptx、26122反比例函数图像和性质教案docx、26122反比例函数的图象和性质同步练习docx等3份课件配套教学资源,其中PPT共0页, 欢迎下载使用。













