初中数学人教版九年级下册第二十六章 反比例函数26.1 反比例函数26.1.2 反比例函数的图象和性质优秀ppt课件

这是一份初中数学人教版九年级下册第二十六章 反比例函数26.1 反比例函数26.1.2 反比例函数的图象和性质优秀ppt课件，共20页。PPT课件主要包含了直线xh，直线x-3，直线x1，直线x3，y2x2，y2x–12，yax2，yax-h2，当向左平移h时，直线x-h等内容，欢迎下载使用。

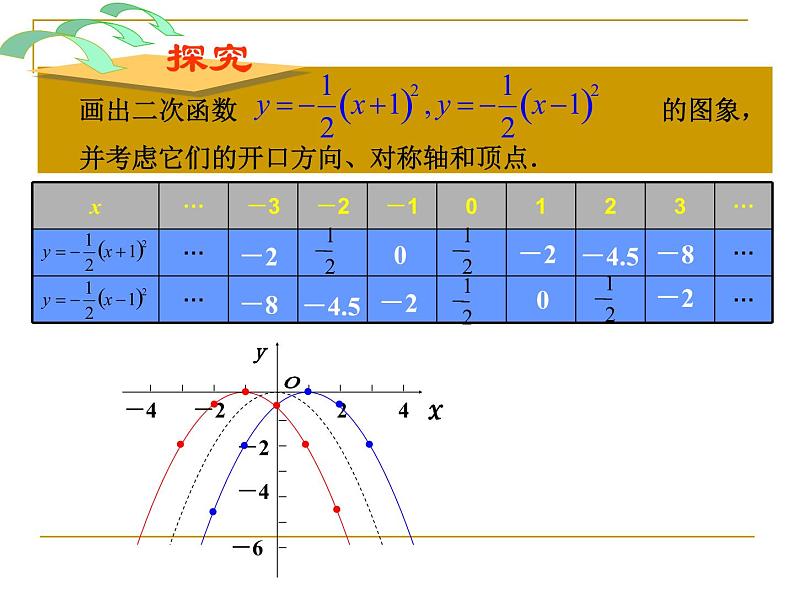
画出二次函数 的图象，并考虑它们的开口方向、对称轴和顶点．
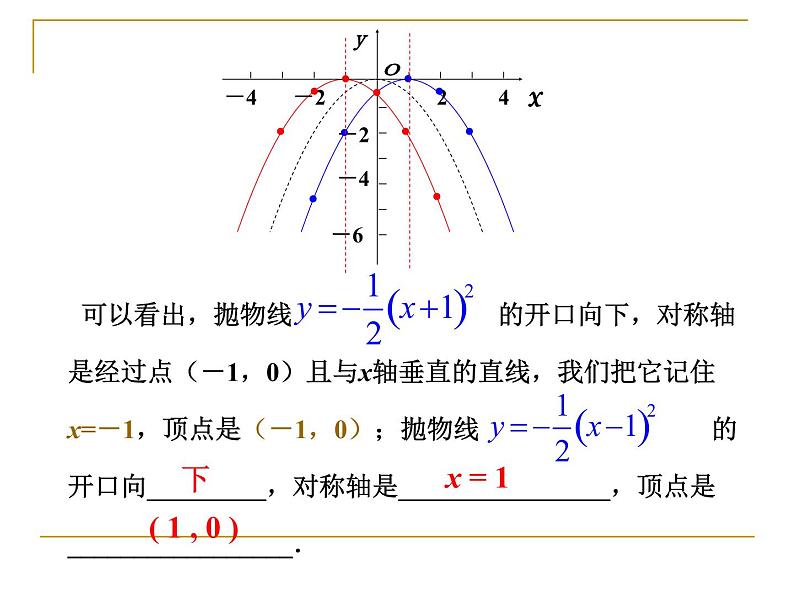
可以看出，抛物线 的开口向下，对称轴是经过点（－1，0）且与x轴垂直的直线，我们把它记住x=－1，顶点是（－1，0）；抛物线 的开口向_________，对称轴是________________，顶点是_________________．
抛物线 与抛物线 有什么关系？
可以发现，把抛物线 向左平移1个单位，就得到抛物线 ；把抛物线 向右平移1个单位，就得到抛物线 ．
练习在同一直角坐标系内画出下列二次函数的图象：
观察三条抛物线的相互关系，并分别指出它们的开口方向、对称轴及顶点．
抛物线 y = a ( x-h)2 的特点：a＞0时，开口________, 最 ____ 点是顶点; a＜0时，开口________, 最 ____ 点是顶点; 对称轴是 _____________， 顶点坐标是 __________。
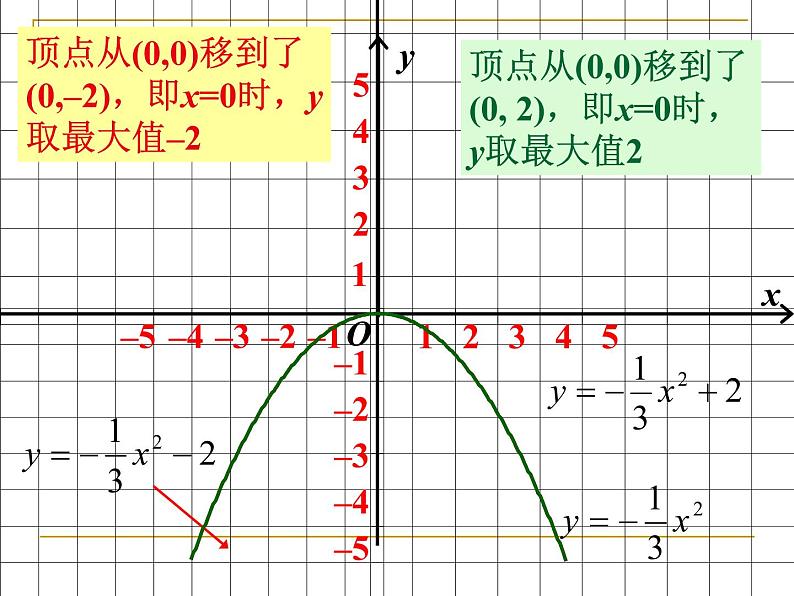
顶点从(0,0)移到了(0,–2)，即x=0时，y取最大值–2
顶点从(0,0)移到了(0, 2)，即x=0时，y取最大值2
顶点从(0,0)移到了(2,0)，即x=2时， y取最大值0
顶点从(0,0)移到了(–2,0)，即x= –2时，y取最大值0
二次函数y=a(x±h)2的图象和性质.
a＞0时，开口_____, 最 ____ 点是顶点; a＜0时，开口_____, 最 ____ 点是顶点; 对称轴是 ， 顶点坐标是 。
y=a(x+h)2的图象
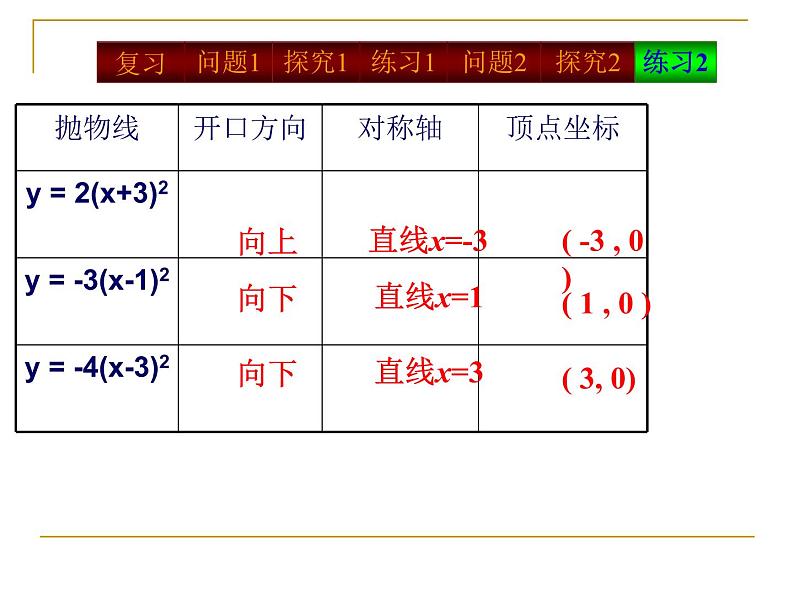
指出下列函数图象的开口方向,对称轴和顶点坐标.
开口 对称轴 顶点坐标
直线x=0 (Y轴)
课堂练习1.抛物线y=0.5(x+2)2可以由抛物线 先向 ( )移2个单位得到。2.已知s= –(x+1)2，当x为 时，s取最 值 为 。3.顶点坐标为(1,0)，且经过(0,-1)的抛物线的函数解析式是( )y=(x+1)2 B. y= –(x+1)2C.y=(x–1)2 D. y= –(x–1)2
抛物线y＝a(x+h)2的性质
（1）对称轴是直线x＝_________
（2）顶点坐标是___________
(3)当a>0时，开口向上，在对称轴的左侧y随x的增大而_______；在对称轴的右侧y随x的增大而________。
（4）当a<0时，开口向下，在对称轴的左侧y随x的增大而_________;在对称轴的右侧y随x的增大而___________
1、函数y=2x2的图象是______线，开口向____，对称轴是_____，顶点坐标是_______，当x=___时，函数有最____值为____；在对称轴左侧， y随x的增大而_______，在对称轴右侧， y随x的增大而_______。
2、函数y=-2x2+4的图象开口向____，对称轴是_____，顶点坐标是_______，当x=____时，函数有最____值为____；当x<0时，y随x的增大而_______，当x>0时， y随x的增大而_______。
3、函数y =-2(x+1)2的图象开口向____，对称轴是____________，顶点坐标是________，当x=____时，函数有最____值为____；当x_____时，y随x的增大而增大，当x_____时， y随x的增大而减小。
4、抛物线y=3x2-4，y=3(x-1)2与抛物线y=3x2的_______相同，_______不同。抛物线y=3x2-4是由抛物线y=3x2向____平移____单位而得到；抛物线y=3(x-1)2是由抛物线y=3x2向____平移____单位而得到。
y = ax2 + k
y = a(x – h )2
如何来求与坐标轴的交点？
求y=x2+2x-8与坐标轴的交点。