初中数学人教版九年级下册26.2 实际问题与反比例函数优秀课件ppt

这是一份初中数学人教版九年级下册26.2 实际问题与反比例函数优秀课件ppt，共39页。PPT课件主要包含了知识点一，与y轴的正半轴相交，与y轴的负半轴相交，经过坐标原点，知识点二，知识点三，点在x轴上方，点在x轴下方，点在x轴上，a+b+c0等内容，欢迎下载使用。
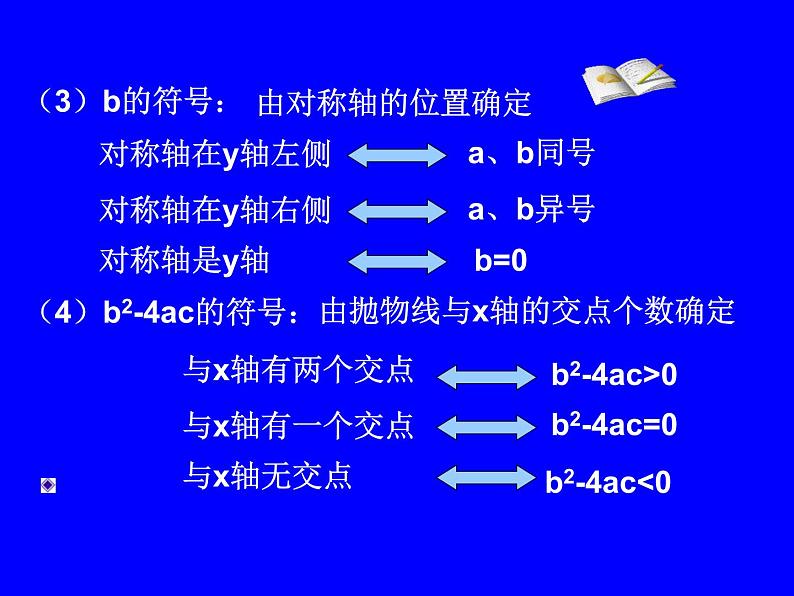
抛物线y=ax2+bx+c的符号问题：
由抛物线的开口方向确定
如果y=ax2+bx+c的图象与x轴的交点为A(x1,0),B(x2,0);那么AB=|x1-x2|=
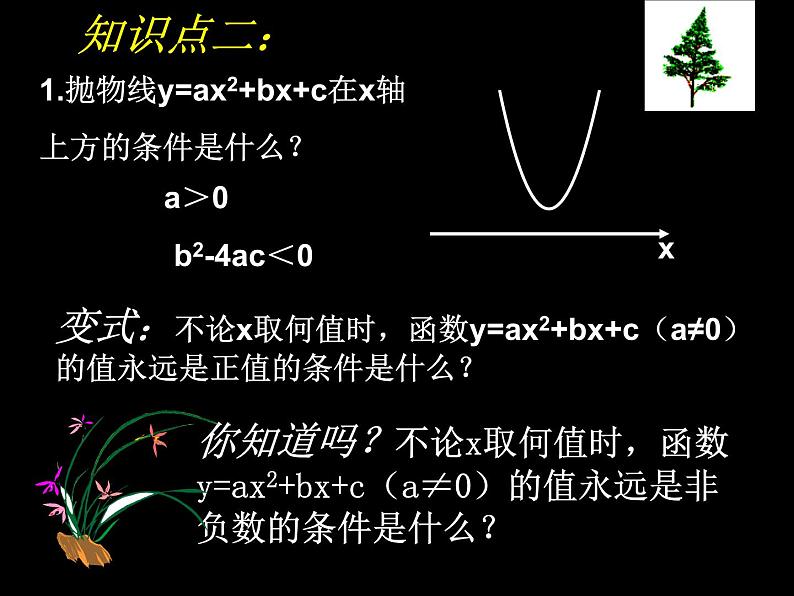
1.抛物线y=ax2+bx+c在x轴上方的条件是什么？
变式：不论x取何值时，函数y=ax2+bx+c（a≠0）的值永远是正值的条件是什么？
你知道吗？不论x取何值时，函数y=ax2+bx+c（a≠0）的值永远是非负数的条件是什么？
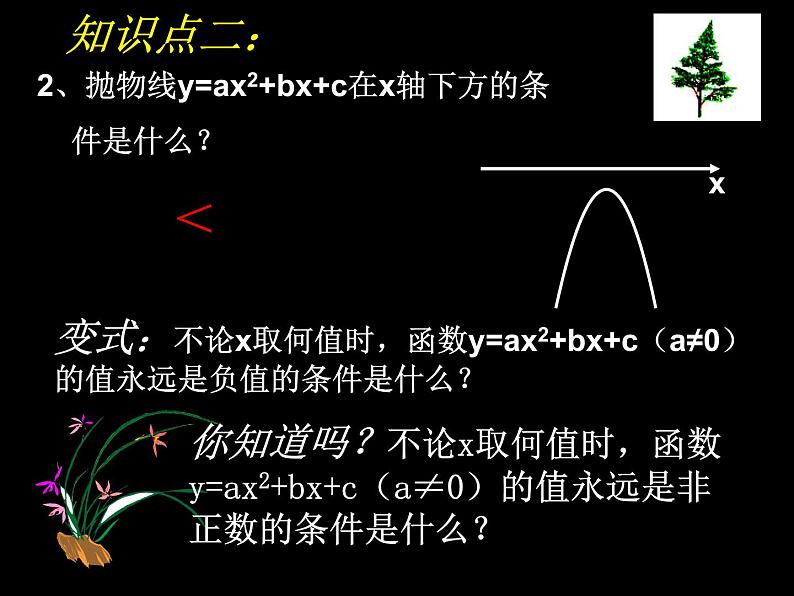
2、抛物线y=ax2+bx+c在x轴下方的条 件是什么？
变式：不论x取何值时，函数y=ax2+bx+c（a≠0）的值永远是负值的条件是什么？
你知道吗？不论x取何值时，函数y=ax2+bx+c（a≠0）的值永远是非正数的条件是什么？
（5）a+b+c的符号：
由x=1时抛物线上的点的位置确定
（6）a-b+c的符号：
由x=-1时抛物线上的点的位置确定
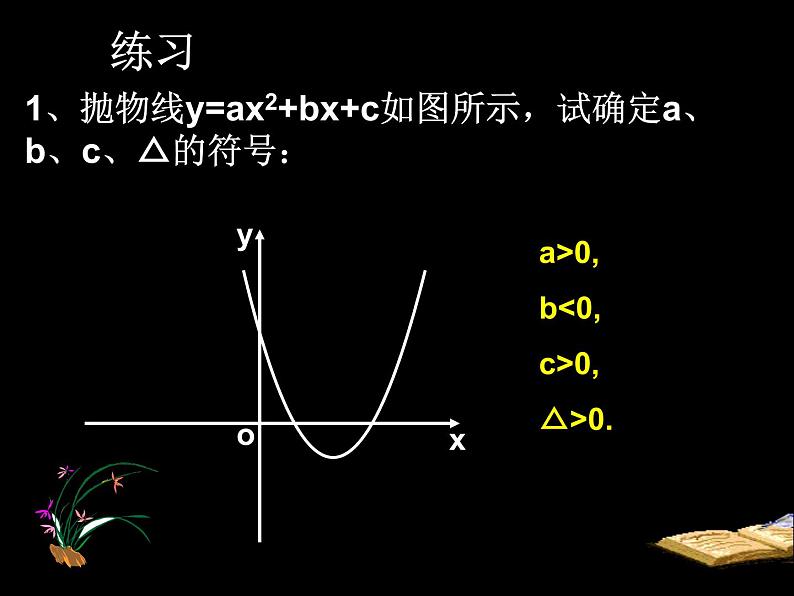
1、抛物线y=ax2+bx+c如图所示，试确定a、b、c、△的符号：
a>0, b0, △>0.
2、抛物线y=ax2+bx+c如图所示，试确定a、b、c、△的符号：
a>0, b>0, c=0, △>0.
3、抛物线y=ax2+bx+c如图所示，试确定a、b、c、△的符号：
a0.
4、抛物线y=ax2+bx+c如图所示，试确定a、b、c、△的符号：
a>0, b=0, c>0, △=0.
5、抛物线y=ax2+bx+c如图所示，试确定a、b、c、△的符号：
a>0, b=0, c=0, △=0.
6、抛物线y=ax2+bx+c如图所示，试确定a、b、c、△的符号：
a0, c0的 解为 　 ( ) A.x > a/b B.x > -a/b C.x < a/b D.x < -a/b
a