






初中26.1.2 反比例函数的图象和性质优秀ppt课件
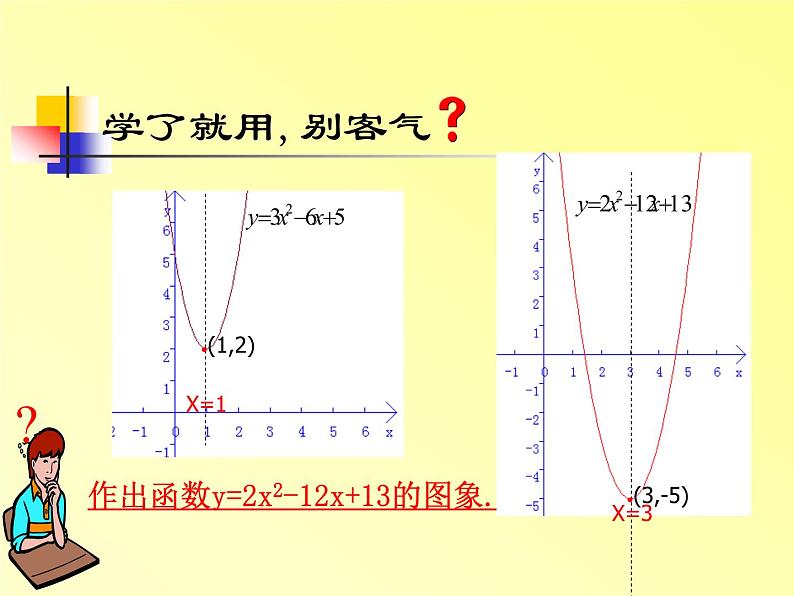
展开怎样直接作出函数y=3x2-6x+5的图象?
函数y=ax²+bx+c的图象
我们知道,作出二次函数y=3x2的图象,通过平移抛物线y=3x2可以得到二次函数y=3x2-6x+5的图象.
配方:加上再减去一次项系数绝对值一半的平方
整理:前三项化为平方形式,后两项合并同类项
老师提示:配方后的表达式通常称为配方式或顶点式
直接画函数y=ax²+bx+c的图象
4.画对称轴,描点,连线:作出二次函数y=3(x-1)2+2的图象.
2.根据配方式(顶点式)确定开口方向,对称轴,顶点坐标.
3.列表:根据对称性,选取适当值列表计算.
∵a=3>0,∴开口向上;对称轴:直线x=1;顶点坐标:(1,2).
作出函数y=2x2-12x+13的图象.
例.求次函数y=ax²+bx+c的对称轴和顶点坐标.
函数y=ax²+bx+c的顶点式
一般地,对于二次函数y=ax²+bx+c,我们可以利用配方法推导出它的对称轴和顶点坐标.
老师提示:这个结果通常称为求顶点坐标公式.
因此,二次函数y=ax²+bx+c的图象是一条抛物线.
根据公式确定下列二次函数图象的对称轴和顶点坐标:
函数y=ax2+bx+c(a≠0)的应用
例:某服装公司试销一种成本为每件50元的T恤衫,规定试销时的销售单价不低于成本价,又不高于每件70元,试销中销售量y(件)与销售单价x(元)的关系可以近似的看作一次函数(如图).(1)求y与x之间的函数关系式;(2)设公司获得的总利润(总利润=总销售额-总成本)为P元,求P与x之间的函数关系式,并写出自变量x的取值范围;根据题意判断:当x取何值时,P的值最大?最大值是多少?
解:(1)设y与x之间的函数关为 ∵经过(60,400)(70,300)∴ 解得: ∴y与x之间的函数关系式为(2)P=(-10x+1000)(x-50)=∴当x=75时,P最大,最大利润为6250元
请你总结函数函数y=ax2+bx+c(a≠0)的图象和性质
想一想,函数y=ax2+bx+c和y=ax2的图象之间的关系是什么?
二次函数y=ax2+bx+c(a≠0)的图象和性质
y=ax2+bx+c(a>0)
y=ax2+bx+c(a<0)
由a,b和c的符号确定
在对称轴的左侧,y随着x的增大而减小. 在对称轴的右侧, y随着x的增大而增大.
在对称轴的左侧,y随着x的增大而增大. 在对称轴的右侧, y随着x的增大而减小.
1.相同点: (1)形状相同(图像都是抛物线,开口方向相同). (2)都是轴对称图形. (3)都有最(大或小)值.(4)a>0时, 开口向上,在对称轴左侧,y都随x的增大而减小,在对称轴右侧,y都随 x的增大而增大. a<0时,开口向下,在对称轴左侧,y都随x的增大而增大,在对称轴右侧,y都随 x的增大而减小 .
2.不同点: (1)位置不同(2)顶点不同:分别是 和(0,0). (3)对称轴不同:分别是 和y轴. (4)最值不同:分别是 和0.3.联系: y=a(x-h)²+k(a≠0) 的图象可以看成y=ax²的图象先沿x轴整体左(右)平移| |个单位(当 >0时,向右平移;当 <0时,向左平移),再沿对称轴整体上(下)平移| |个单位 (当 >0时向上平移;当 <0时,向下平移)得到的.
二次函数y=ax2+bx+c(a≠0)与=ax²的关系
1.确定下列二次函数的开口方向、对称轴和顶点坐标.
用待定系数法求二次函数解析式,要根据给定条件的特点选择合适的方法来求解
一般地,在所给条件中已知顶点坐标时,可设顶点式y=a(x-h)2+k,在所给条件中已知抛物线与x轴两交点坐标或已知抛物线与x轴一交点坐标与对称轴,可设交点式y=a(x-x1)(x-x2);在所给的三个条件是任意三点时,可设一般式y=ax2+bx+c;然后组成三元一次方程组来求解。
例:已知关于x的二次函数,当x=-1时,函数值为10,当x=1时,函数值为4,当x=2时,函数值为7,求这个二次函数的解析试.
例:根据下列条件,分别求出对应的二次函数解析式
(1)已知抛物线的顶点是(1,2)且过点(2,3)
(2)已知抛物线与x轴两交点横坐标为1,3且图像过(0,-3)
已知顶点坐标设顶点式y=a(x-h)2+k∵顶点是(1,2)∴设y=a(x-1)2+2,又过点(2,3)∴a(2-1)2+2=3,∴a=1∴ y=(x-1)2+2,即y=x2-2x+3
已知与x轴两交点横坐标,设交点式y=a(x-x1)(x-x2)由抛物线与x轴两交点横坐标为1,3,∴设y=a(x-1)(x-3),过(0,-3),∴ a(0-1)(0-3)=-3, ∴a=-1∴ y=-(x-1)(x-3),即y=-x2+4x-3
(3)已知二次函数的图像过(-1,2),(0,1),(2,-7)
已知普通三点设一般式y=ax2+bx+c,设y=ax2+bx+c过(-1,2),(0,1),(2,-7)三点∴
例:已知一抛物线与x轴的交点A(-2,0),B(1,0)且经过点C(2,8)(1)求该抛物线的解析式 (2)求该抛物线的顶点坐标
解:设这个抛物线的表达式为Y=ax2+bx+c
由已知,抛物线过点(-2,0),B(1,0),C(2,8)三点,得
所以该抛物线的表达式为y=2x2+2x-4
(2)y=2x2+2x-4=2(x2+x-2)=2(x+1/2)2-9/2
所以该抛物线的顶点坐标为(-1/2,-9/2)
例:如图,已知二次函数 的图像经过点A和点B.(1)求该二次函数的表达式;(2)写出该抛物线的对称轴及顶点坐标;(3)点P(m,m)与点Q均在该函数图像上(其中m>0),且这两点关于抛物线的对称轴对称,求m的值及点Q 到x轴的距离.
解:(1)将x=-1,y=-1;x=3,y=-9分别代入 得 解得∴二次函数的表达式为.(2)对称轴为 ;顶点坐标为(2,-10).(3)将(m,m)代入 ,得 ,解得 .∵m>0,∴ 不合题意,舍去.∴ m=6.∵点P与点Q关于对称轴 对称,∴点Q到x轴的距离为6.
初中数学人教版九年级下册第二十六章 反比例函数26.1 反比例函数26.1.1 反比例函数精品ppt课件: 这是一份初中数学人教版九年级下册第二十六章 反比例函数26.1 反比例函数26.1.1 反比例函数精品ppt课件,共27页。PPT课件主要包含了一条直线,一条抛物线,自变量x不能为0,①列表,②描点,③连线,y减小,第四象限等内容,欢迎下载使用。
初中人教版26.1.2 反比例函数的图象和性质课前预习ppt课件: 这是一份初中人教版26.1.2 反比例函数的图象和性质课前预习ppt课件,共18页。PPT课件主要包含了y随x的增大而增大,y随x的增大而减小,当k0时,函数图象画法,描点法等内容,欢迎下载使用。
2021学年26.1.2 反比例函数的图象和性质优质ppt课件: 这是一份2021学年26.1.2 反比例函数的图象和性质优质ppt课件,共20页。PPT课件主要包含了学习目标,新课导入,知识点,反比例函数的图象,如何画函数的图象,函数图象画法,描点法,新知探索,当k>0时,当k<0时等内容,欢迎下载使用。













