初中数学人教版八年级下册18.1.2 平行四边形的判定一等奖ppt课件

这是一份初中数学人教版八年级下册18.1.2 平行四边形的判定一等奖ppt课件，共25页。PPT课件主要包含了学习目标，新课导入，新课讲解，课堂小结，当堂小练，拓展与延伸，布置作业，复习引入，连接AC，BCDA已知等内容，欢迎下载使用。
1.经历平行四边形判定定理的猜想与证明过程，体会 类比思想及探究图形判定的一般思路；（重点）2.掌握平行四边形的三个判定定理，能根据不同条件 灵活选取适当的判定定理进行推理论证.（难点）
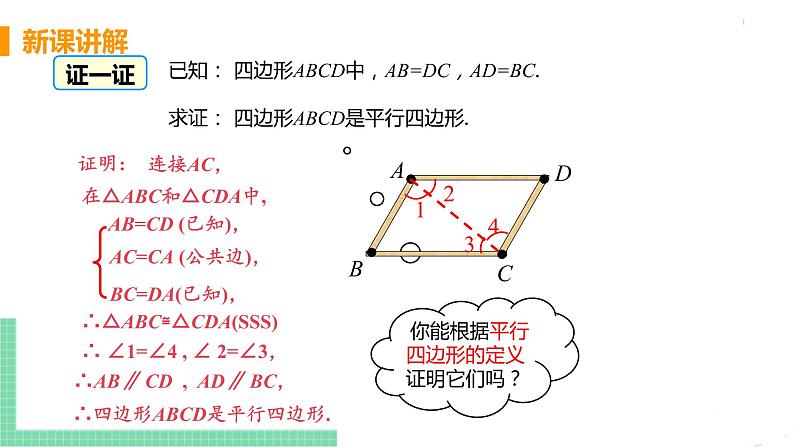
两组对边分别平行的四边形叫平行四边形.
问题1 平行四边形的定义是什么？有什么作用？
可以用平行四边形的定义来判定平行四边形，如：
知识点1 两组对边分别相等的四边形是平行四边形
猜想 观看视频，将两长两短的四根细木条用小钉固定在一起,任意拉动，所得的四边形是平行四边形吗?
你能根据平行四边形的定义证明它们吗？
已知： 四边形ABCD中，AB=DC，AD=BC.求证： 四边形ABCD是平行四边形.
在△ABC和△CDA中,
AB=CD (已知)，
AC=CA (公共边)，
∴△ABC≌△CDA(SSS)
∴ ∠1=∠4 , ∠ 2=∠3，
∴AB∥ CD , AD∥ BC，
∴四边形ABCD是平行四边形.
平行四边形的判定定理：两组对边分别相等的四边形是平行四边形.
几何语言描述：在四边形ABCD中，∵AB=CD,AD=BC,∴四边形ABCD是平行四边形.
例1 如图，在Rt△MON中，∠MON＝90°.求证：四边形PONM是平行四边形．
证明：Rt△MON中，由勾股定理得(x－5)2＋42＝(x－3)2， 解得x＝8.∴PM＝11－x＝3，ON＝x－5＝3，MN＝x－3＝5.∴PM＝ON，OP＝MN，∴四边形PONM是平行四边形．
例2 如图，在△ABC中，分别以AB、AC、BC为边在BC的同侧作等边△ABD、等边△ACE、等边△BCF.试说明四边形DAEF是平行四边形．
解：∵△ABD和△FBC都是等边三角形，∴∠DBF＋∠FBA＝∠ABC＋∠ABF＝60°， ∴∠DBF＝∠ABC.又∵BD＝BA，BF＝BC，∴△ABC≌△DBF(SAS)，∴AC＝DF＝AE.同理可证△ABC≌△EFC，∴AB＝EF＝AD，∴四边形DAEF是平行四边形．
如图, AD⊥AC,BC⊥AC,且AB=CD,求证：四边形ABCD是平行四边形.
证明：在Rt△ABC和Rt△ACD中，∵AC=CA,AB=CD,∴Rt△ABC≌Rt△CDA(HL),∴BC=DA.又∵AB=CD,∴四边形PONM是平行四边形．
知识点2 两组对角分别相等的四边形是平行四边形
观看下面视频，对于两组对角分别相等的四边形的形状你的猜想是什么?
已知：四边形ABCD中，∠A=∠C，∠B=∠D，求证：四边形ABCD是平行四边形.
又∵∠A=∠C，∠B=∠D，
∵∠A+∠C+∠B+∠D=360°，
∴2∠A+2∠B=360°，
即∠A+∠B=180°，
同理得 AB∥ CD，
平行四边形的判定定理：两组对角分别相等的四边形是平行四边形.
几何语言描述：在四边形ABCD中，∵∠A=∠C，∠B=∠D,∴四边形ABCD是平行四边形.
例3 如图，四边形ABCD中，AB∥DC，∠B＝55°，∠1＝85°，∠2＝40°.(1)求∠D的度数；(2)求证：四边形ABCD是平行四边形．
(1)解：∵∠D＋∠2＋∠1＝180°，∴∠D＝180°－∠2－∠1＝55°；(2)证明：∵AB∥DC，∴∠2＝∠CAB，∴∠DAB＝∠1＋∠2＝125°.∵∠DCB＋∠DAB＋∠D＋∠B＝360°，∴∠DCB＝∠DAB＝125°.又∵∠D＝∠B＝55°，∴四边形ABCD是平行四边形．
1.判断下列四边形是否为平行四边形：
2.能判定四边形ABCD是平行四边形的条件： ∠A:∠B:∠C:∠D的值为 （　　）
A. 1:2:3:4
B. 1:4:2:3
C. 1:2:2:1
D. 3:2:3:2
知识点3 对角线互相平分的四边形是平行四边形
如图,将两根细木条AC、BD的中点重叠，用小钉固定在一起，用橡皮筋连接木条的顶点，做成一个四边形ABCD.转动两根木条，四边形ABCD一直是一个平行四边形吗？
猜想：四边形ABCD一直是一个平行四边形.
已知：四边形ABCD中，OA=OC，OB=OD.求证：四边 形ABCD是平行四边形.
在△AOB和△COD中,
OA=OC (已知)，
OB=OD (已知)，
∠AOB=∠COD (对顶角相等)，
∴△AOB≌△COD(SAS)，
∴ ∠BAO=∠OCD , ∠ ABO=∠CDO,
∴AB∥ CD , AD∥ BC
平行四边形的判定定理：对角线互相平分的四边形是平行四边形.
几何语言描述：在四边形ABCD中，∵AO=CO,DO=BO,∴四边形ABCD是平行四边形.
例4 如图， □ABCD 的对角线AC,BD相交于点O,E,F是AC上的两点，并且AE=CF.求证：四边形BFDE是平行四边形.
证明：∵四边形ABCD是平行四边形，
∴ AO=CO,BO=DO.
∴ AO-AE=CO-CF,即EO=OF.
∴四边形BFDE是平行四边形.
定义法:两组对边分别平行的四边形叫平行四边形.
两组对边分别相等的四边形是平行四边形.
两组对角分别相等的四边形是平行四边形.
对角线互相平分的四边形是平行四边形.
1.判断对错:(1)有一组对边平行的四边形是平行四边形. ( ) (2)有两条边相等，并且另外的两条边也相等的四边 形一定是平行四边形. ( )(3)对角线互相平分的四边形是平行四边形. ( ) (4)一条对角线平分另一条对角线的四边形是平行四 边形. ( )(5)有一组对角相等且一组对边平行的四边形是平行 四边形. ( )
2.如图，四边形ABCD的对角线交于点O，下列哪组条件不能判断四边形ABCD是平行四边形（　　）A．OA=OC，OB=OD B．AB=CD，AO=CO C．AB=CD，AD=BC D．∠BAD=∠BCD，AB∥CD
3.如图，在四边形ABCD中，
(1)如果AB∥CD，AD∥BC，那么四边形ABCD是 ___________.(2)如果∠A：∠B：∠ C：∠D=a：b：a：b(a,b为正 数),那么四边形ABCD是__________.
(3)如果AD=6cm,AB=4cm,那么当BC=_______cm, CD=_____cm时,四边形ABCD为平行四边形.
4.如图，五边形ABCDE是正五边形，连接BD、CE，交于点P． 求证：四边形ABPE是平行四边形．
证明：∵五边形ABCDE是正五边形，∴正五边形的每个内角的度数是 AB=BC=CD=DE=AE，∴∠DEC=∠DCE= ×(180°-108°)=36°，同理∠CBD=∠CDB=36°，∴∠ABP=∠AEP=108°-36°=72°，∴∠BPE=360°-108°-72°-72°=108°=∠A，∴四边形ABPE是平行四边形．