初中数学人教版八年级下册18.1.2 平行四边形的判定优秀ppt课件

这是一份初中数学人教版八年级下册18.1.2 平行四边形的判定优秀ppt课件，共24页。PPT课件主要包含了学习目标，新课导入，新课讲解，课堂小结，当堂小练，拓展与延伸，布置作业，复习引入，对角线，概念学习等内容，欢迎下载使用。
1.理解三角形中位线的概念，掌握三角形的中位线 定理.（重点）2.能利用三角形的中位线定理解决有关证明和计算问题.(重点）
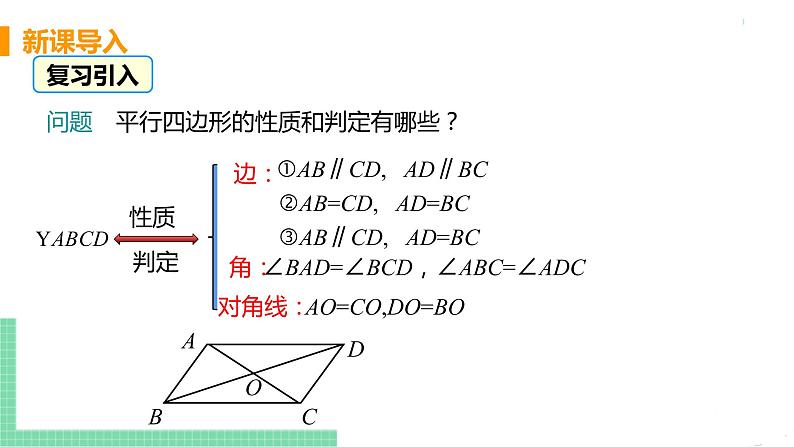
问题 平行四边形的性质和判定有哪些？
AB∥CD, AD∥BC
AB=CD, AD=BC
AB∥CD, AD=BC
∠BAD=∠BCD，∠ABC=∠ADC
AO=CO,DO=BO
知识点1 三角形的中位线定理
定义：连接三角形两边中点的线段叫做三角形的中位线.
如图，在△ABC中，D、E分别是AB、AC的中点，连接DE.则线段DE就称为△ABC的中位线.
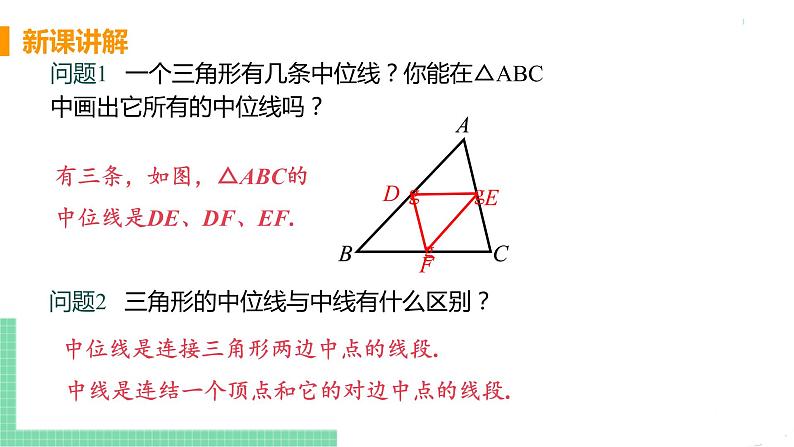
问题1 一个三角形有几条中位线？你能在△ABC中画出它所有的中位线吗？
有三条，如图，△ABC的中位线是DE、DF、EF.
问题2 三角形的中位线与中线有什么区别？
中位线是连接三角形两边中点的线段.
中线是连结一个顶点和它的对边中点的线段.
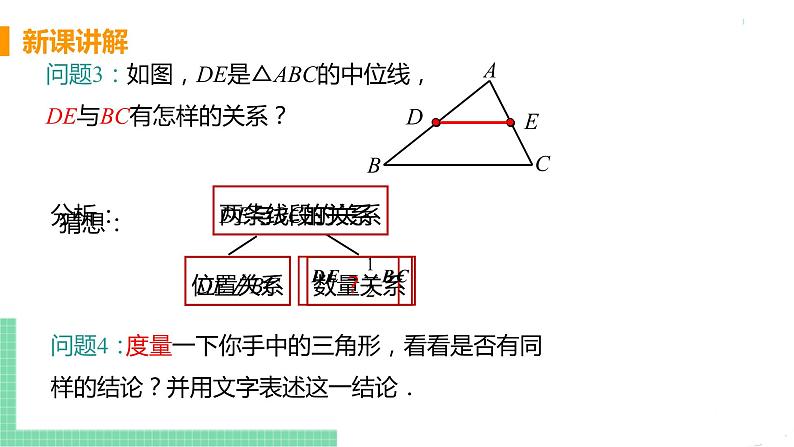
问题3：如图，DE是△ABC的中位线，DE与BC有怎样的关系？
度量一下你手中的三角形，看看是否有同样的结论？并用文字表述这一结论．
一条线段是另一条线段的一半
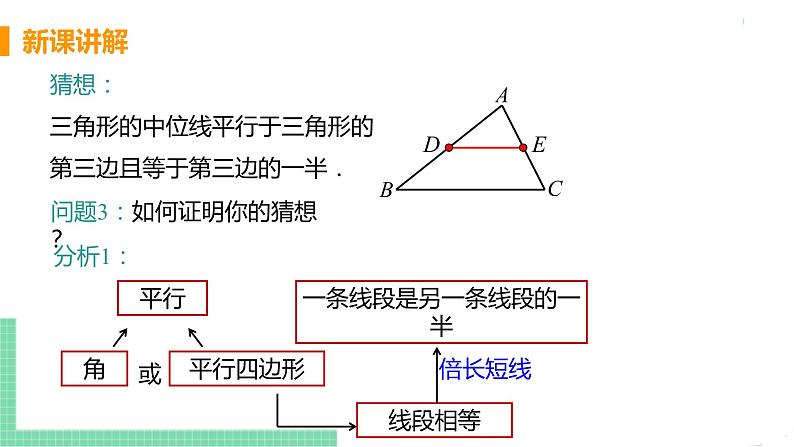
猜想：三角形的中位线平行于三角形的第三边且等于第三边的一半．
问题3：如何证明你的猜想？
延长DE到F，使EF=DE．
连接AF、CF、DC ．
∵AE=EC，DE=EF ，
∴四边形ADCF是平行四边形．
∴四边形BCFD是平行四边形，
∴ DE∥BC， ．
如图，在△ABC中，点D,E分别是AB,AC边的中点，求证：
三角形的中位线平行于三角形的第三边且等于第三边的一半．
①中位线DE、EF、DF把△ABC分成四个全等的三角形；有三组共边的平行四边形，它们是四边形ADFE和BDEF，四边形BFED和CFDE，四边形ADFE和DFCE.
②顶点是中点的三角形，我们称之为中点三角形；中点三角形的周长是原三角形的周长的一半.面积等于原三角形面积的四分之一.
由此你知道怎样分蛋糕了吗
例1 如图，在△ABC中，D、E分别为AC、BC的中点，AF平分∠CAB，交DE于点F.若DF＝3，求AC的长
解：∵D、E分别为AC、BC的中点，∴DE∥AB，∴∠2＝∠3.又∵AF平分∠CAB，∴∠1＝∠3，∴∠1＝∠2，∴AD＝DF＝3，∴AC＝2AD＝2DF＝6.
1. 如图，△ABC中，D、E分别是AB、AC中点．
（1） 若DE=5，则BC= ．
（2） 若∠B=65°，则∠ADE= °．
（3） 若DE+BC=12，则BC= ．
2.如图，A，B两点被池塘隔开，在A，B外选一点C，连接AC和BC，并分别找出AC和BC的中点M，N，如果测得MN=20m，那么A，B两点间的距离为______m．
知识点2 三角形的中位线的与平行四边形的综合运用
例4 如图，在四边形ABCD中，E、F、G、H分别是AB、BC、CD、DA中点．求证：四边形EFGH是平行四边形．
∵E,F,G,H分别为各边的中点,
∴ EF∥HG, EF=HG.
∴四边形EFGH是平行四边形.
顺次连结四边形四条边的中点，所得的四边形是平行四边形.
【变式题】如图，E、F、G、H分别为四边形ABCD四边之中点．求证：四边形EFGH为平行四边形.
证明：如图，连接BD.∵E、F、G、H分别为四边形ABCD四边之中点，∴EH是△ABD的中位线， FG是△BCD的中位线，∴EH∥BD且EH= BD， FG∥BD且FG= BD，∴EH∥FG且EH=FG，∴四边形EFGH为平行四边形.
三角形中位线平行于第三边，并且等于它的一半
三角形的中位线定理的应用
2.如图，在▱ABCD中，AD=8，点E，F分别是BD，CD的中点，则EF等于 （　　）A.2 B.3 C.4 D.5
1.如图，在△ABC中，点E、F分别为AB、AC的中点．若EF的长为2，则BC的长为 （　　）A.1 B.2 C.4 D.8
3.如图，点 D、E、F 分别是 △ABC 的三边AB、BC、 AC的中点.（1）若∠ADF=50°，则∠B= °；（2）已知三边AB、BC、AC分别为12、10、8， 则△ DEF的周长为 .
4.在△ABC中，E、F、G、H分别为AC、CD、 BD、 AB的中点，若AD=3，BC=8，则四边形EFGH的周长是 .
5.如图，在△ABC中，AB=6cm，AC=10cm，AD平分∠BAC，BD⊥AD于点D，BD的延长线交AC于 点F，E为BC的中点，求DE的长．
解：∵AD平分∠BAC，BD⊥AD，∴AB=AF=6，BD=DF，∴CF=AC-AF=4，∵BD=DF，E为BC的中点，∴DE= CF=2．