人教版八年级下册18.2.3 正方形公开课课件ppt

这是一份人教版八年级下册18.2.3 正方形公开课课件ppt，共31页。PPT课件主要包含了学习目标，新课导入，新课讲解，课堂小结，当堂小练，拓展与延伸，布置作业，情景引入，问题引入，正方形等内容，欢迎下载使用。
1.理解正方形的概念.2.探索并证明正方形的性质，并了解平行四边形、矩形、菱形之间的联系和区别.(重点、难点)3.会应用正方形的性质解决相关证明及计算问题.（难点）4.探索并证明正方形的判定，并了解平行四边形、矩形、菱形之间的联系和区别；(重点、难点)
观察下面图形,正方形是我们熟悉的几何图形，在生活中无处不在.
你还能举出其他的例子吗？
知识点1 正方形的性质
矩 形
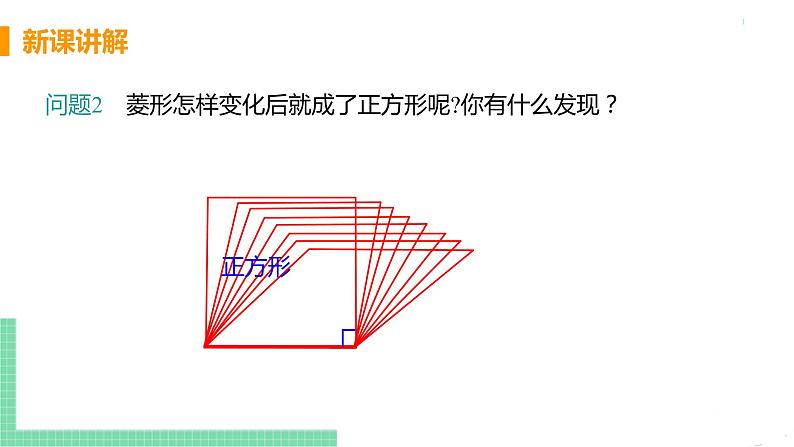
问题1：矩形怎样变化后就成了正方形呢?你有什么 发现？
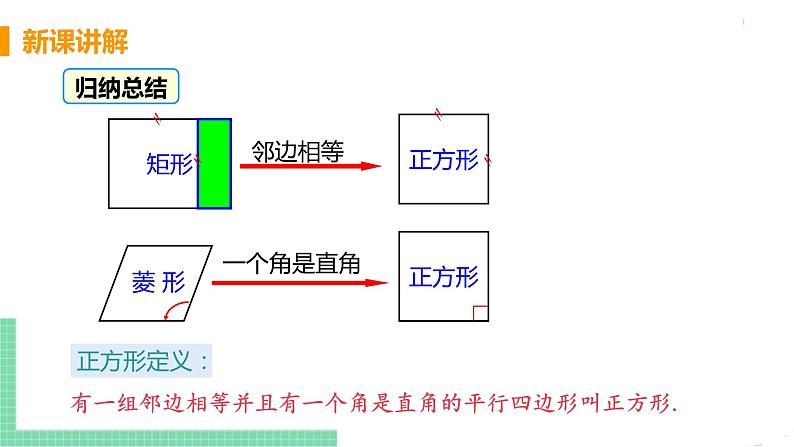
问题2 菱形怎样变化后就成了正方形呢?你有什么发现？
有一组邻边相等并且有一个角是直角的平行四边形叫正方形.
已知：如图,四边形ABCD是正方形.求证：正方形ABCD四边相等,四个角都是直角.
证明：∵四边形ABCD是正方形.∴∠A=90°, AB=AC （正方形的定义）. 又∵正方形是平行四边形.∴正方形是矩形（矩形的定义）, 正方形是菱形(菱形的定义).∴∠A=∠B =∠C =∠D = 90°, AB= BC=CD=AD.
已知：如图,四边形ABCD是正方形.对角线AC、BD相交于点O.求证：AO=BO=CO=DO,AC⊥BD.
证明：∵正方形ABCD是矩形, ∴AO=BO=CO=DO. ∵正方形ABCD是菱形. ∴AC⊥BD.
思考 请同学们拿出准备好的正方形纸片,折一折,观察并思考.  正方形是不是轴对称图形?如果是,那么对称轴有几条?
对称性： .对称轴：.
正方形是特殊的平行四边形,也是特殊的矩形,也是特殊的菱形.所以矩形、菱形有的性质,正方形都有.
平行四边形、矩形、菱形、正方形之间关系：
性质：1.正方形的四个角都是直角,四条边相等. 2.正方形的对角线相等且互相垂直平分.
例1 求证: 正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.
已知: 如图,四边形ABCD是正方形,对角线AC、BD相 交于点O.
求证: △ABO、 △BCO、 △CDO、 △DAO是全等的等腰直角三角形.
证明: ∵ 四边形ABCD是正方形,∴ AC=BD,AC⊥BD,AO=BO=CO=DO.∴ △ABO、 △BCO、 △CDO、 △DAO都是等腰直角三角形,并且△ABO≌ △BCO ≌ △CDO ≌ △DAO.
例2 如图，在正方形ABCD中， ΔBEC是等边三角形， 求证： ∠EAD＝∠EDA＝15° .
证明：∵ ΔBEC是等边三角形，∴BE=CE=BC,∠EBC=∠ECB=60°，∵ 四边形ABCD是正方形，∴AB=BC=CD,∠ABC=∠DCB=90°，∴AB=BE=CE=CD, ∠ABE= ∠DCE=30°，∴△ABE，△DCE是等腰三角形， ∴∠BAE= ∠BEA= ∠CDE= ∠CED=75°，∴∠EAD= ∠EDA=90°-75°=15°.
1.正方形具有而矩形不一定具有的性质是 ( ) A.四个角相等 B.对角线互相垂直平分 C.对角互补 D.对角线相等
2.正方形具有而菱形不一定具有的性质（ ） A.四条边相等 B.对角线互相垂直平分 C.对角线平分一组对角 D.对角线相等
知识点2 正方形的判定
活动1 准备一张矩形的纸片，按照下图折叠,然后展开，折叠部分得到一个正方形，可量一量验证验证.
猜想 满足怎样条件的矩形是正方形？
已知：如图,在矩形ABCD中,AC , DB是它的两条对角线, AC⊥DB.求证：四边形ABCD是正方形.证明：∵四边形ABCD是矩形, ∴ AO=CO=BO=DO ，∠ADC=90°. ∵AC⊥DB, ∴ AD=AB=BC=CD, ∴四边形ABCD是正方形.
对角线互相垂直的矩形是正方形.
活动2 把可以活动的菱形框架的一个角变为直角，观察这时菱形框架的形状.量量看是不是正方形.
猜想 满足怎样条件的菱形是正方形？
已知：如图,在菱形ABCD中,AC , DB是它的两条对角线, AC=DB.求证：四边形ABCD是正方形.证明：∵四边形ABCD是菱形,∴AB=BC=CD=AD,AC⊥DB.∵AC=DB,∴ AO=BO=CO=DO,∴△AOD,△AOB,△COD,△BOC是等腰直角三角形，∴∠DAB=∠ABC=∠BCD=∠ADC=90°, ∴四边形ABCD是正方形.
对角线相等的菱形是正方形.
正方形判定的几条途径：
在四边形ABCD中，O是对角线的交点，能判定这个四边形是正方形的是（ ）
A．AC=BD，AB∥CD，AB=CDB．AD∥BC，∠A=∠CC．AO=BO=CO=DO，AC⊥BDD．AO=CO，BO=DO，AB=BC
例1 在正方形ABCD中，点E、F、M、N分别在各边上，且AE=BF=CM=DN．四边形EFMN是正方形吗?为什么?
证明：∵四边形ABCD是正方形，∴AB=BC=CD=DA，∠A=∠B=∠C=∠D=90°.∵AE=BF=CM=DN，∴AN=BE=CF=DM.
分析：由已知可证△AEN≌△BFE≌△CMF≌△DNM，得四边形EFMN是菱形，再证有一个角是直角即可.
在△AEN、△BFE、△CMF、△DNM中， AE=BF=CM=DN, ∠A=∠B=∠C=∠D, AN=BE=CF=DM,∴△AEN≌△BFE≌△CMF≌△DNM,∴EN=FE=MF=NM，∠ANE=∠BEF,∴四边形EFMN是菱形， ∠NEF=180°－（∠AEN+∠BEF） =180°－（∠AEN+∠ANE） =180°－90°=90°.∴四边形EFMN是正方形 .
思考 前面学菱形时我们探究了顺次连接任意四边形各边中点所得的四边形是平行四边形.顺次连接矩形各边中点能得到菱形，那么顺次连接正方形各边中点能得到怎样的特殊平行四边形？
3.对角线相等且互相垂直平分
有一组邻相等，并且有一个角是直角的平行四边形叫做正方形.
一个角是直角且一组邻边相等
平行四边形、矩形、菱形、正方形的判定小结
1.下列命题正确的是（ ） A.四个角都相等的四边形是正方形 B.四条边都相等的四边形是正方形 C.对角线相等的平行四边形是正方形 D.对角线互相垂直的矩形是正方形
3．在正方形ABC中,∠ADB= ,∠DAC= , ∠BOC= .4.在正方形ABCD中，E是对角线AC上一点，且AE=AB，则∠EBC的度数是 .
5.一个正方形的对角线长为2cm，则它的面积是 （　　）A.2cm2 B.4cm2 C.6cm2 D.8cm2
4.平行四边形、矩形、菱形、正方形都具有的是（　） A．对角线互相平分 B．对角线互相垂直 C．对角线相等 D．对角线互相垂直且相等
5.如图，正方形ABCD的边长为1cm，AC为对角线，AE平分∠BAC，EF⊥AC，求BE的长．
解：∵四边形ABCD为正方形，∴∠B＝90°，∠ACB＝45°，AB＝BC＝1cm.∵EF⊥AC，∴∠EFA＝∠EFC＝90°.又∵∠ECF＝45°，∴△EFC是等腰直角三角形，∴EF＝FC.∵∠BAE＝∠FAE，∠B＝∠EFA＝90°，AE＝AE，∴△ABE≌△AFE，∴AB＝AF＝1cm，BE＝EF.∴FC＝BE.在Rt△ABC中，∴FC＝AC－AF＝( －1)cm，∴BE＝( －1)cm．
6.如图，△ABC中，D是BC上任意一点，DE∥AC，DF∥AB．（1）试说明四边形AEDF的形状，并说明理由．（2）连接AD，当AD满足什么条件时，四边形AEDF为菱形，为什么？
解：（1）∵DE∥AC，DF∥AB，∴四边形AEDF为平行四边形.（2）∵四边形AEDF为菱形，∴AD平分∠BAC，则AD平分∠BAC时，四边形AEDF为菱形.