




初中数学人教版九年级下册28.2 解直角三角形及其应用精品课件ppt
展开1. 巩固解直角三角形有关知识. (重点)2. 能运用解直角三角形知识解决仰角和俯角有关的实 际问题,在解题过程中进一步体会数形结合、转化、 方程的数学思想,并从这些问题中归纳出常见的基 本模型及解题思路. (重点、难点)
某探险者某天到达如图所示的点A 处时,他准备估算出离他的目的地,海拔为3 500 m的山峰顶点B处的水平距离.他能想出一个可行的办法吗? 通过这节课的学习,相信你也行.
知识点1 解与仰俯角有关的问题
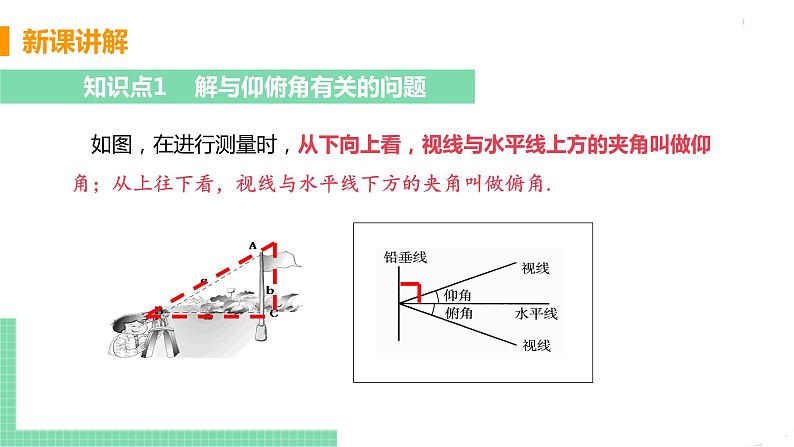
如图,在进行测量时,从下向上看,视线与水平线上方的夹角叫做仰角;从上往下看,视线与水平线下方的夹角叫做俯角.
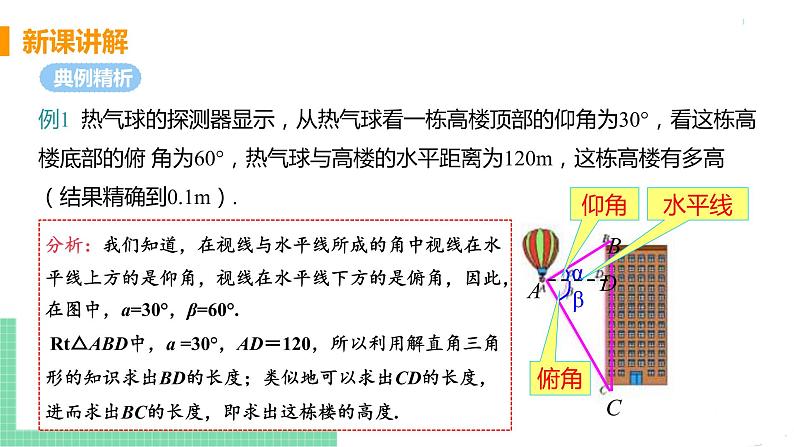
例1 热气球的探测器显示,从热气球看一栋高楼顶部的仰角为30°,看这栋高楼底部的俯 角为60°,热气球与高楼的水平距离为120m,这栋高楼有多高(结果精确到0.1m).
分析:我们知道,在视线与水平线所成的角中视线在水平线上方的是仰角,视线在水平线下方的是俯角,因此,在图中,a=30°,β=60°. Rt△ABD中,a =30°,AD=120,所以利用解直角三角形的知识求出BD的长度;类似地可以求出CD的长度,进而求出BC的长度,即求出这栋楼的高度.
解:如图,a = 30°,β= 60°, AD=120.
答:这栋楼高约为277.1m.
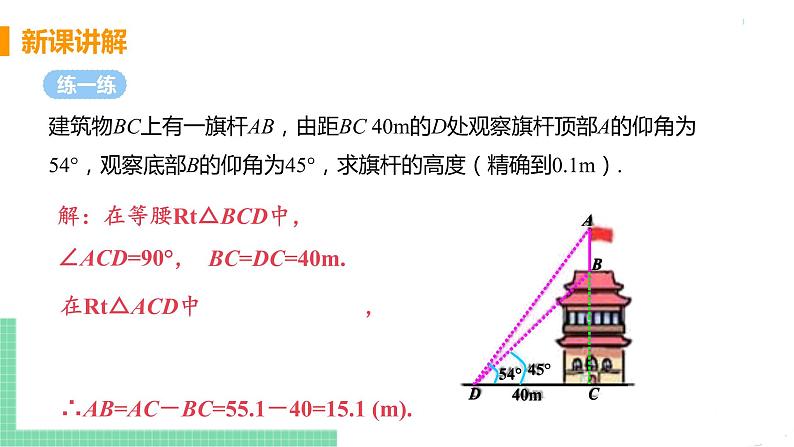
建筑物BC上有一旗杆AB,由距BC 40m的D处观察旗杆顶部A的仰角为54°,观察底部B的仰角为45°,求旗杆的高度(精确到0.1m).
解:在等腰Rt△BCD中,∠ACD=90°,
∴AB=AC-BC=55.1-40=15.1 (m).
例2 如图,小明想测量塔AB的高度.他在D处仰望塔顶,测得仰角为30°,再往塔的方向前进50m至C处.测得仰角为60°,小明的身高1.5 m.那么该塔有多高?(结果精确到1 m),你能帮小明算出该塔有多高吗?
分析:由图可知,塔高AB可以分为两部分,上部分AB′可以在Rt△AD′B′和Rt△AC′B′中利用仰角的正切值求出,B′B与D′D相等.
解:如图,由题意可知,∠AD′B′=30°,∠AC′B′=60°, D′C′=50m.∴ ∠D′AB′=60°,∠C′AB′=30°,D′C′=50m ,设AB′=x m.
利用仰俯角解直角三角形
运用解直角三角形解决仰角、俯角问题
仰角、俯角问题的常见基本模型:
1. 如图①,在高出海平面100米的悬崖顶A处,观测海平 面上一艘小船B,并测得它的俯角为45°,则船与观 测者之间的水平距离BC=_________米.2. 如图②,两建筑物AB和CD的水平距离为30米,从A点 测得 D点的俯角为30°,测得C点的俯角为60°,则 建筑物CD的高为_____米.
3. 为测量松树AB的高度,一个人站在距松树15米的E 处,测得仰角∠ACD=52°,已知人的高度是1.72米, 则树高 (精确到0.1米).
4. 如图,在电线杆上离地面高度5m的C点处引两根拉线固定电线杆,一根拉线AC和地面成60°角,另一 根拉线BC和地面成45°角.则两根拉线的总长度为 m(结果用带根号的数的形式表示).
解:由题意,AC=AB=610(米).
数学九年级下册28.2 解直角三角形及其应用多媒体教学ppt课件: 这是一份数学九年级下册28.2 解直角三角形及其应用多媒体教学ppt课件,共25页。PPT课件主要包含了知识回顾,学习目标,课堂导入,新知探究,最远点,跟踪训练,随堂练习,实际问题,数学问题,数学问题的答案等内容,欢迎下载使用。
初中数学人教版九年级下册28.2 解直角三角形及其应用优秀课件ppt: 这是一份初中数学人教版九年级下册28.2 解直角三角形及其应用优秀课件ppt,共29页。PPT课件主要包含了知识回顾,学习目标,课堂导入,新知探究,跟踪训练,i113,i2125,随堂练习,解直角三角形的应用,方向角问题等内容,欢迎下载使用。
初中数学人教版九年级下册第二十八章 锐角三角函数28.2 解直角三角形及其应用完美版课件ppt: 这是一份初中数学人教版九年级下册第二十八章 锐角三角函数28.2 解直角三角形及其应用完美版课件ppt,共25页。PPT课件主要包含了知识回顾,学习目标,课堂导入,新知探究,最远点,跟踪训练,随堂练习,实际问题,数学问题,数学问题的答案等内容,欢迎下载使用。













