初中数学第二章 二次函数1 二次函数完美版课件ppt

这是一份初中数学第二章 二次函数1 二次函数完美版课件ppt，共19页。PPT课件主要包含了学习目标，数形结合直观感受，描点连线，yx2，观察图象回答问题，在学中做在做中学，y-x2，1完成下表，只是开口大小不同，练习与提高等内容，欢迎下载使用。

1、会用描点法画二次函数y=x2和y=-x2的图象；
2、根据函数y=x2和y=-x2的图象，直观地了解它的性质.
你想直观地了解它的性质吗?
在二次函数y=x2中,y随x的变化而变化的规律是什么？
观察y=x2的表达式,选择适当x值,并计算相应的y值,完成下表：
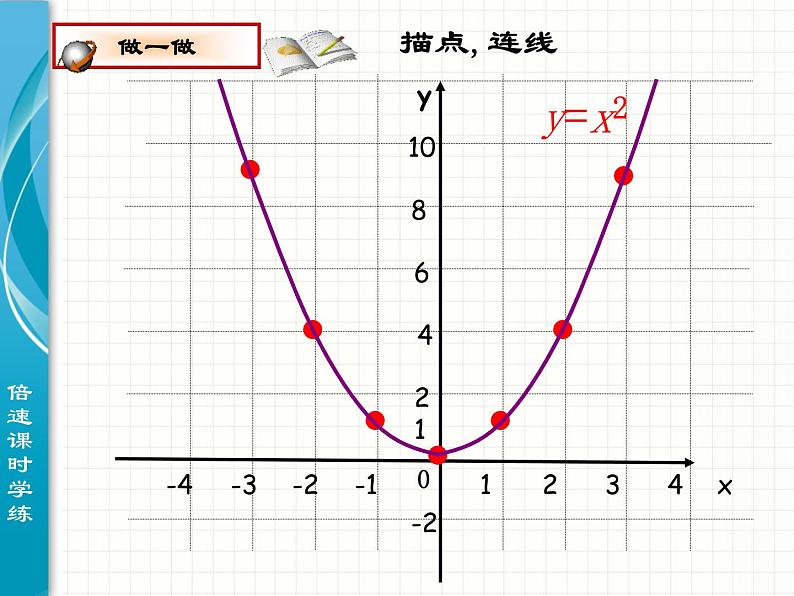
你会用描点法画二次函数y=x2的图象吗?
(1)你能描述图象的形状吗?与同伴进行交流.
(5)图象是轴对称图形吗？如果是,它的对称轴是什么?请你找出几对对称点,并与同伴交流.
(2)图象 与x轴有交点吗？如果有,交点坐标是什么?
(3)当x<0时,随着x的值增大,y 的值如何变化？当x>0呢？
(4)当x取什么值时,y的值最小?最小值是什么？你是如何知道的？
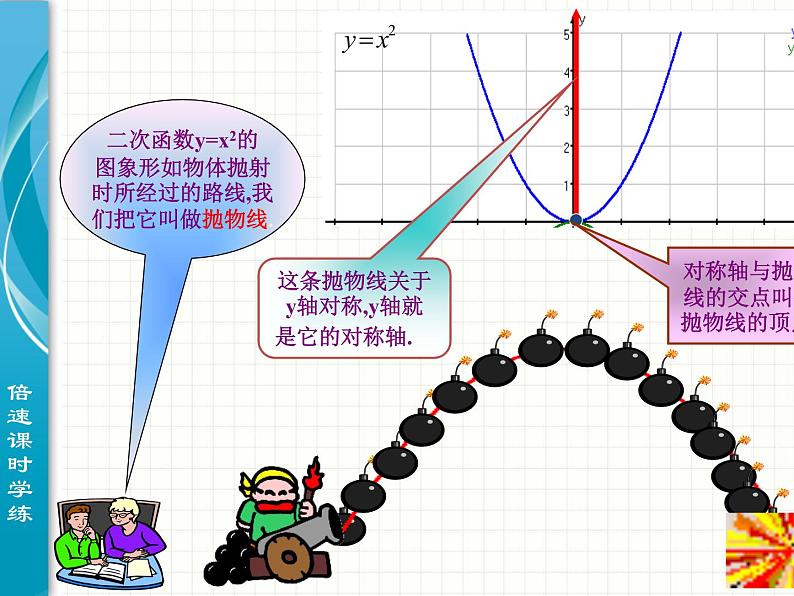
这条抛物线关于y轴对称,y轴就 是它的对称轴.
对称轴与抛物线的交点叫做抛物线的顶点.
二次函数y=x2的图象形如物体抛射时所经过的路线,我们把它叫做抛物线.
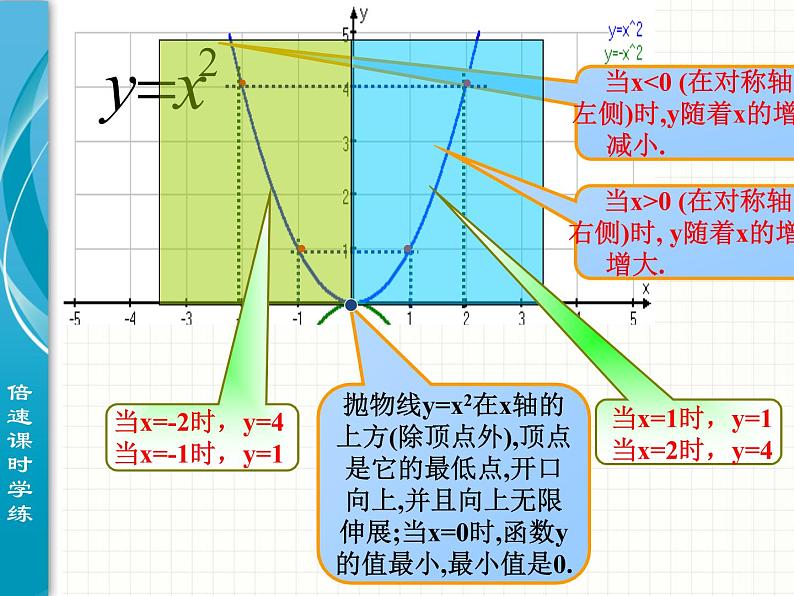
当x<0 (在对称轴的左侧)时,y随着x的增大而减小.
当x>0 (在对称轴的右侧)时, y随着x的增大而增大.
抛物线y=x2在x轴的上方(除顶点外),顶点是它的最低点,开口向上,并且向上无限伸展;当x=0时,函数y的值最小,最小值是0.
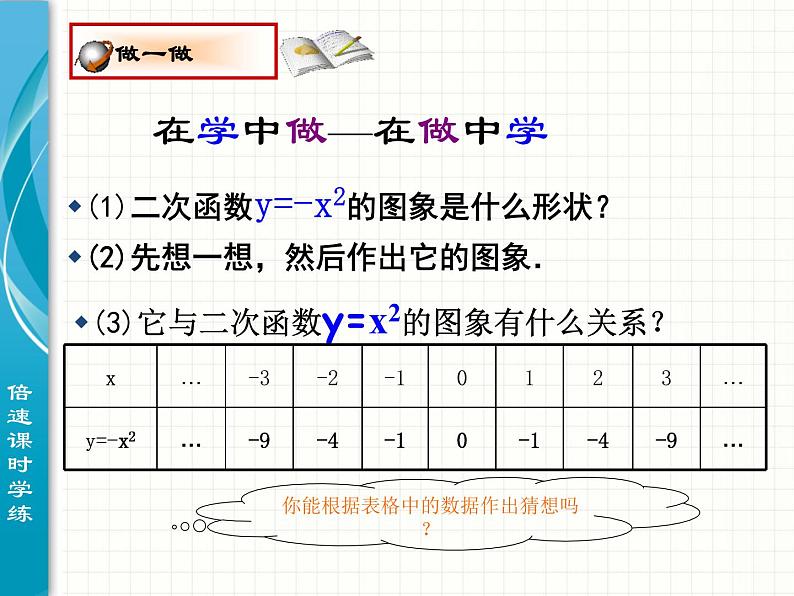
(1)二次函数y=-x2的图象是什么形状？
你能根据表格中的数据作出猜想吗？
(2)先想一想，然后作出它的图象．
(3)它与二次函数y=x2的图象有什么关系？
函数y=ax2(a≠0)的图象和性质:
二次函数y=ax2的性质
当x=0时,y最小值为0.
当x=0时,y最大值为0.
当x<0, y随着x的增大而减小. 当x>0 , y随着x的增大而增大.
当x<0,y随着x的增大而增大. 当x>0 , y随着x的增大而减小.
函数y=ax2(a≠0)的图象和性质
在同一坐标系中作二次函数y=x2和y=2x2的图象．
(2)分别作出y=x2和y=2x2的图象．
二次项系数a>0,开口都向上;对称轴都是y轴;增减性与也相同.
顶点都是原点(0,0).
二次函数y=2x2的图象形状与y=x2一样,仍是抛物线.
(3)二次函数y=2x2的图象是什么形状?它与二次函数y=x2的图象有什么相同和不同?它的开口方向、对称轴和顶点坐标分别是什么?
想一想,在同一坐标系中作二次函数y=-x2和y=-2x2的图象,会是什么样?
二次项系数a<0,开口都向下;对称轴都是y轴;增减性与也相同.
二次函数y=-2x2的图象形状与y=-x2一样,仍是抛物线.
(4)二次函数y=-2x2的图象是什么形状?它与二次函数y=-x2的图象有什么相同和不同?它的开口方向、对称轴和顶点坐标分别是什么?
请你总结二次函数y=ax2的图象和性质.
(1)开口方向及大小:
当a>0时,开口向上。
当a<0时，开口向下。
若a>0, y有最小值，当x=0时，y最小=0
若a<0，y有最大值，当x=0时，y最大=0
若a>0,当x<0时，y值随x值的增大而减小； 当x>0时，y值随x值的增大而增大。
若a<0,当x<0时，y值随x值的增大而增大； 当x>0时，y值随x值的增大而减小。
1、已知函数 是关于x 的二次函数。求： （1）满足条件的m 的值； （2）m为何值时，抛物线有最低点？求出这个最低点， 这时当x 为何值时，y 随x 的增大而增大？（3）m为何值时，函数有最大值？最大值是多少？ 这时当x 为何值时，y 随x 的增大而减小？
1.已知抛物线y=ax2经过点A（-2，-8）. （1）求此抛物线的函数解析式； （2）判断点B（-1，- 4）是否在此抛物线上. （3）求出此抛物线上纵坐标为-6的点的坐标.
解（1）把（-2，-8）代入y=ax2,得 -8=a(-2)2,解得a= -2,所求函数解析式为y= -2x2.
2.填空:(1)抛物线y=2x2的顶点坐标是 ,对称轴是 ,在 侧,y随着x的增大而增大；在 侧,y随着x的增大而减小,当x=_____时,函数y的值最小,最小值是 ,
(2)抛物线 在x轴的 方(除顶点外),在对称轴的左侧,y随着x的 ；在对称轴的右侧,y随着x的 ,当x=0时,函数y的值最大,最大值是 ,