九年级下册第二章 二次函数1 二次函数一等奖课件ppt

这是一份九年级下册第二章 二次函数1 二次函数一等奖课件ppt，共15页。PPT课件主要包含了直线与圆的位置关系，有三种位置关系，直线和圆相交，直线和圆相切，直线和圆相离，由此你能悟出点什么，∴∠A60°等内容，欢迎下载使用。

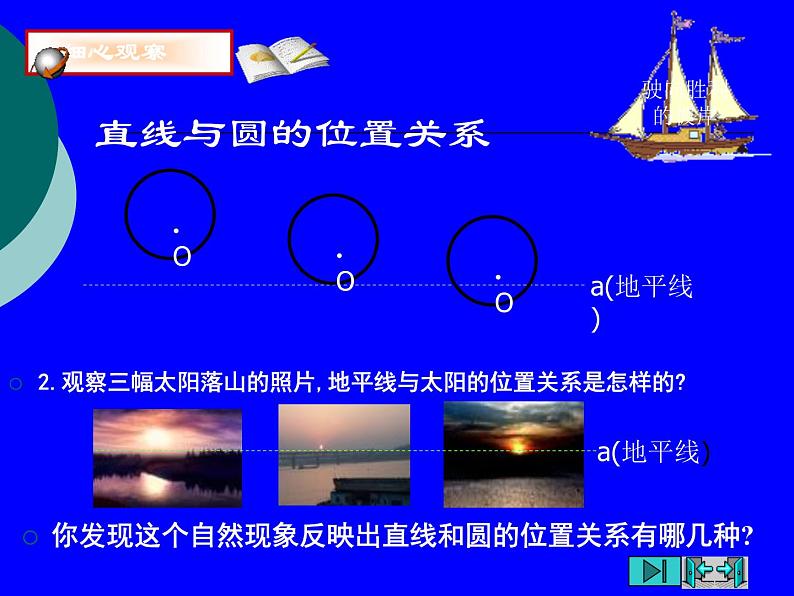
1.观察三幅太阳升起的照片,地平线与太阳的位置关系是怎样的?
你发现这个自然现象反映出直线和圆的位置关系有哪几种?
2.观察三幅太阳落山的照片,地平线与太阳的位置关系是怎样的?
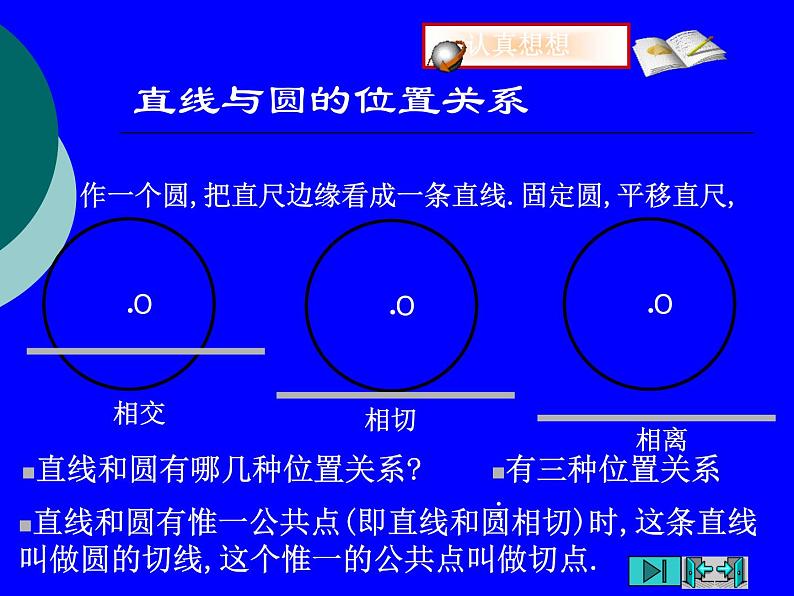
作一个圆,把直尺边缘看成一条直线.固定圆,平移直尺,
直线和圆有哪几种位置关系?
直线和圆有惟一公共点(即直线和圆相切)时,这条直线叫做圆的切线,这个惟一的公共点叫做切点.
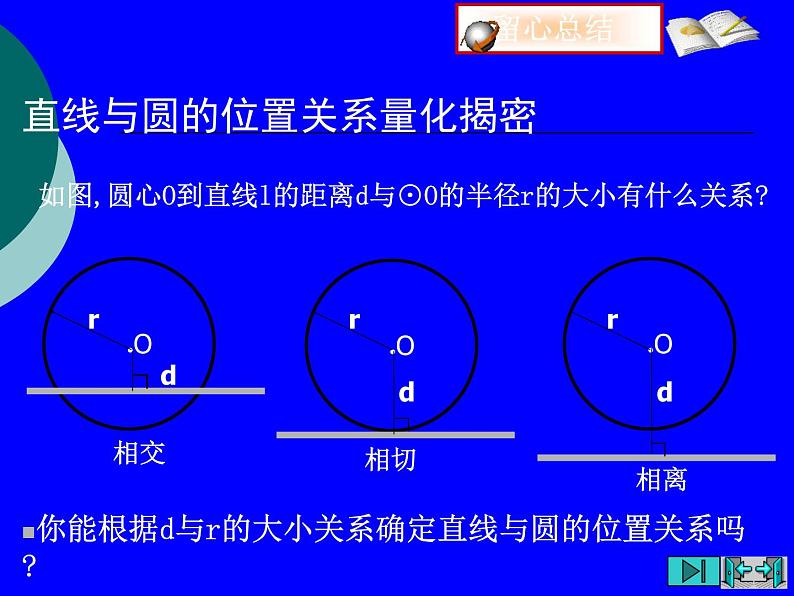
如图,圆心O到直线l的距离d与⊙O的半径r的大小有什么关系?
你能根据d与r的大小关系确定直线与圆的位置关系吗?
直线与圆的位置关系量化揭密
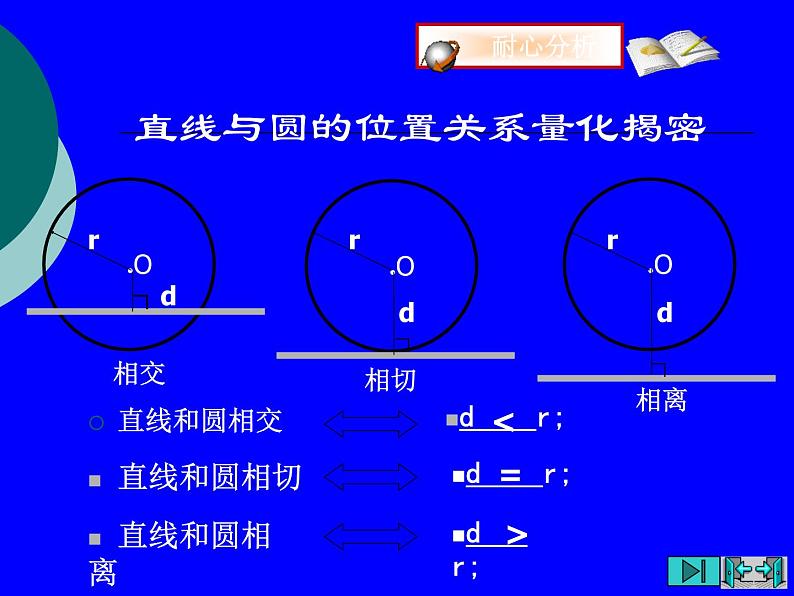
直线与圆的位置关系量化揭密
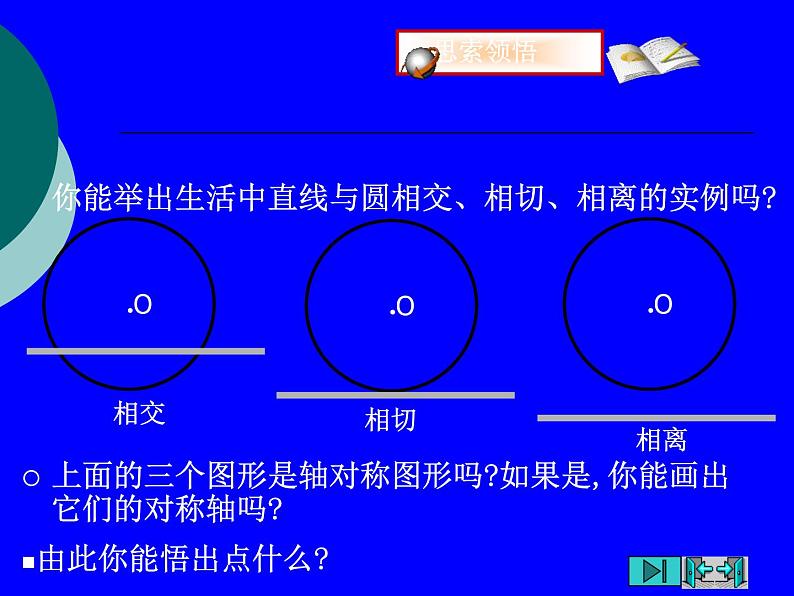
你能举出生活中直线与圆相交、相切、相离的实例吗?
上面的三个图形是轴对称图形吗?如果是,你能画出它们的对称轴吗?
如图,直线CD与⊙O相切于点A,直径AB与直线CD有怎样的位置关系?说说你的理由.
直径AB垂直于直线CD.
老师期望:圆的对称性已经在你心中落地生根.
小颖的理由是:∵右图是轴对称图形,AB是对称轴,∴沿直线AB对折图形时,AC与AD重合,因此,∠BAC=∠BAD=90°.
小亮的理由是:直径AB与直线CD要么垂直,要么不垂直.
假设AB与CD不垂直,过点O作一条直径垂直于CD,垂足为M,
老师期望:你能看明白(或掌握)用反证法说理的过程.
则OM参考小颖和小亮的说理过程,请你写出这个命题
圆的切线垂直于过切点的半径。
老师提示:切线的性质是证明两线垂直的重要根据;作过切点的半径是常用的辅助线之一.
如图∵CD是⊙O的切线,A是切点,OA是⊙O的半径,∴CD⊥OA.
1.已知Rt△ABC的斜边AB=8cm,直角边AC=4cm.
(1)以点C为圆心作圆,当半径为多长时,AB与⊙C相切?
老师提示:模型“双垂直三角形”你可曾认识？
解:(1)过点C作CD⊥AB于D.
∵AB=8cm,AC=4cm.
(2)以点C为圆心,分别以2cm,4cm为半径作两个圆,这两个圆与AB分别有怎样的位置关系?
当r=4cm时,d当r=2cm时,d>r,AB与⊙C相离;
1.直线BC与半径为r的⊙O相交,且点O到直线BC的距离为5,求r的取值范围.
2.一枚直径为d的硬币沿直线滚动一圈.圆心经过的距离是多少?.
老师提示:硬币滚动一圈,圆心经过的路经是与直线平行的一条线段,其长度等于圆的周长.
1.已知:如图,P是⊙O外一点,PA,PB都是⊙O的切线,A,B是切点.请你观察猜想,PA,PB有怎样的关系?并证明你的结论.
2.由1所得的结论及证明过程,你还能发现那些新的结论?如果有,仍请你予以证明.
老师提示:根据这个结论写出的命题称为切线长定理及其推论.