北师大版七年级下册6 完全平方公式优质ppt课件

这是一份北师大版七年级下册6 完全平方公式优质ppt课件，共35页。PPT课件主要包含了公式的结构特征，左边是，a2−b2，两个二项式的乘积，右边是，两数的平方差，平方差公式，a2+2ab+b2，a2-2ab+b2，a2＋2ab＋b2等内容，欢迎下载使用。
(a+b)(a−b)=
即两数和与这两数差的积.
一、完全平方公式的推导1.两数和的平方.(a+b)2=(a+b)(a+b)=___________=_________.2.两数差的平方.(a-b)2=(a-b)(a-b)=___________=_________.
a2+ab+ab+b2
a2-ab-ab+b2
【归纳】(1)(a＋b)2＝___________，(a－b)2＝___________.(2)公式特征：①左边：二项式的和的_____;②右边是三项,且有___个平方项,中间项为首尾两项底数积的2倍.(3)语言叙述：两数和(或差)的平方,等于这两个数的_______,加上(或减去)这两数的___的2倍.
前平方，后平方，二倍乘积在中央；同号加，异号减，符号置于中间项
二、几何解释如图,最大正方形的面积可用两种形式表示：①______，②_________，由于这两个代数式表示同一块面积,所以应相等,即______= _________.【点拨】公式中的a和b可代表一个字母、一个数字、单项式或多项式.
=a2 −2ab+b2.
= 2 + 2 + 2
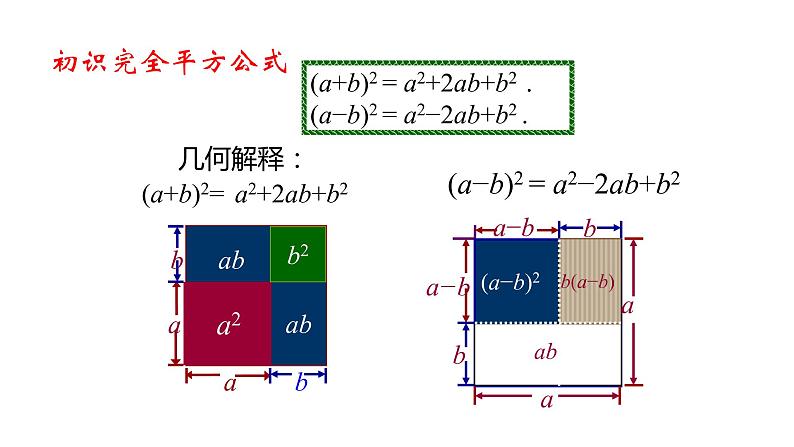
初识完全平方公式
(a+b)2 = a2+2ab+b2 .(a−b)2 = a2−2ab+b2 .
(a−b)2 = a2−2ab+b2
(a+b)2 +(a-b)2 =2(a2+b2)
完全平方公式的常见变形
例1 利用完全平方公式计算：(2x−3)2 ；(2) (4x+5y)2 ; (3) (mn−a)2
(a-b)2= a2 - 2 a b + b2
= 4x2-12x+9
2x看作是a,3看作是b
解: (4x+5y)2=
(a +b)2= a2 + 2 ab + b2
+ 2(4x)(5y)
(2) (4x+5y)2
=16x2 +40xy +25y2
4x看作是a,5y看作是b
(3) (mn−a)2
=（mn）2-2×mn×a+a2
mn看作是a,a看作是b
=m2n2-2amn+a2
(a -b)2= a2 - 2 a b + b2
1、使用完全平方公式与平方差公式一样,先要把计算的式子与完全平方公式对照,明确哪个是 a , 哪个是 b。
2、公式中的字母a，b可以表示数，也可以表示单项式和多项式.
（1）(-2x+1)2
方法1：把-2x看作a，1看作b解：原式=(-2x)2+2(-2x).1+12
方法2： 解：原式=（1-2x)2
=12-2×1×2x+(2x)2
方法3：解：原式=[-(2x-1)]2
(2)(-1-2x)2
把1看作a，2x看作b
把2x看作a，1看作b
方法1：解：原式=(-1)2-2(-1)(2x)+(2x)2
方法3： 解：原式=[-(1+2x)]2
=12+2×1×2x+(2x)2
方法2：解：原式=[(-1)+(-2x)]2
=(-1)2+2(-1)(-2x)+(-2x)2
把-1看作a，2x看作b
把-1看作a，-2x看作b
1、利用完全平方公式计算：
(1)(m +3)2(2)(3x-2)2(3) ( x − 2y)2 (4) (2xy+ x )2
= x2-2xy+4y2
=4x2y2+4x2y+x2
解：原式＝(4x2－9)2＝16x4－72x2＋81
说说：下面各式的计算是否正确？请把错误的改正
(1)(x+y)2=x2+y2
(2)(2x-3y)2=2x2- 2(2x)(3y)+3y2
(3)(m-n)2=m2+2mn+n2
(4) (2a-b)2=(2a)2-2ab+b2
(x+y)2 =x2+2xy +y2
(2x-3y)2 =(2x)2-2(2x)(3y) +(3y)2
(m-n)2=m2-2mn +n2
(2a-b)2 =(2a)2-2(2a)b +b2
改错： 指出下列各式中的错误，并加以改正：(1) (2a−1)2＝2a2−2a+1;(2) (2a+1)2＝4a2 +1；(3) (a−1)2＝a2−2a−1.
第一数被平方时, 未添括号;
第一数与第二数乘积的2倍 少乘了一个2 ;
应改为: (2a−1)2＝ (2a)2−2•2a•1+1;
(2) 少了第一数与第二数乘积的2倍 (丢了一项);
应改为: (2a+1)2＝ (2a)2+2•2a•1 +1;
(3) 第一数平方未添括号,
第一数与第二数乘积的2倍 错了符号;
第二数的平方 这一项错了符号;
应改为: (a−1)2＝(a)2−2•(a )•1+12;
1) a2+ +b2=(a+b)22) a2+ +b2=(a - b)23) 4a2+ +b2=(2a+b)24) 4a2+ +b2=(2a - b)25) ( )2+4ab+b2=( +b)26) a2-8ab+ =( )2
7.如果 x2 +mx+4是完全平方式,那么 m的值是多少?
完全平方公式【例1】化简：(a-b)2+b(2a+b).【解题探究】(1)(a-b)2化简后的结果为a2-2ab+b2.(2)b(2a+b)化简后的结果为2ab+b2.所以原式=a2-2ab+b2+2ab+b2=a2+2b2.
注意完全平方公式和平方差公式不同：
完全平方公式的结果 是三项， 即 (a b)2＝a2 2ab+b2;
平方差公式的结果 是两项， 即 (a+b)(a−b)＝a2−b2.
在解题过程中要准确确定a和b、对照公式原形的两边, 做到不丢项、不弄错符号、2ab时不少乘2；首项、末项是乘积被平方时要注意添括号, 是运用完全平方公式进行多项式乘法的关键.
课外作业：计算：(1)(－m－n)2. (2)(－5a－2)(5a＋2).【解析】(1)(－m－n)2＝(－m)2＋2(－m)(－n)＋(－n)2＝m2＋2mn＋n2.(2)(－5a－2)(5a＋2)＝－(5a＋2)(5a＋2)＝－(5a＋2)2＝－(25a2＋20a＋4)＝－25a2－20a－4.
1.8 完全平方公式第2课时
（1） 305² （2） 198² （3） 95 ² （4） 19²
比一比赛一赛看谁做的又对又快!
例2 计算：(1) (x+3)2 - x2
你能用几种方法进行计算?试一试。
解:方法一： 完全平方公式合并同类项
(x+3)2-x2= x2＋6x+9-x2 = 6x+9
解:方法二： 平方差公式单项式乘多项式.
(x+3)2-x2=(x+3+x)(x+3-x)=(2x+3)·3=6x+9


#k#b#1#新#课#

例2计算:(2)(x+5)2–(x-2)(x-3)
解: (x+5)2-(x-2)(x-3)
=(x2+10x+25)-(x2-5x+6)
= x2+10x+25-x2+5x-6
温馨提示：1.注意运算的顺序。2.(x−2)(x−3)展开后的结果要注意添括号。
例3 计算：(3)(a+b+3)(a+b-3)
(a+b+3) (a+b−3)
=( )2− 32
=a2 +2ab+b2－9
温馨提示：将(a+b)看作一个整体，解题中渗透了整体的数学思想。
[ (a+b) +3] [ (a+b) -3]
练习．计算：(1)(3x－y)2(y＋3x)2；解：原式＝[(3x－y)(3x＋y)]2＝(9x2－y2)2＝81x4－18x2y2＋y4(2)(2x＋y－2)(2x＋y＋2)．解：原式＝(2x＋y)2－4＝4x2＋4xy＋y2－4
计算：(x+y)(x-y)(x2-y2)解：原式=(x2-y2)(x2-y2) =(x2-y2)2 =x4-2x2y2+y4
完全平方公式的应用【例4】已知x+y=8，xy=12，求x2+y2的值.【解题探究】(1)因为x+y=8，所以(x+y)2的值是64.(2)由完全平方公式可知(x+y)2=x2+2xy+y2，由上述探究可得x2+2xy+y2=64，即x2+y2=64-2xy.(3)由已知xy=12可得x2+y2=64-2×12=40.
1、已知： 求： 和 的值
把所得结果作为推广了的完全平方公式，试用语言叙述这一公式：
三个数和的完全平方等于这三个数的平方和，再加上每两数乘积的2倍。
仿照上述结果，你能说出(a−b+c)2所得的结果吗?
(m+n+p)2=[(m+n)+p]2
=(m+n)2+2(m+n)p+p2
=m2+2mn+n2+2mp+2np+p2
=m2+ n2 +p2+2mn+2mp+2np
1.已知a+b=5,ab=4,求a2+b2的值，提示[利用公式(a+b)2=a2+2ab+b2]
又∵a+b=5,ab=4,∴(a+b)2=25；2ab=8
解 ∵(a+b)2=a2+2ab+b2
∴a2+b2=(a+b)2-2ab
∴a2+b2=(a+b)2-2ab =25-8=17
你能算出（a-b)2的值吗？