初中数学北师大版八年级下册2 直角三角形优秀ppt课件

这是一份初中数学北师大版八年级下册2 直角三角形优秀ppt课件，共23页。PPT课件主要包含了做一做，直角边，本节小结等内容，欢迎下载使用。

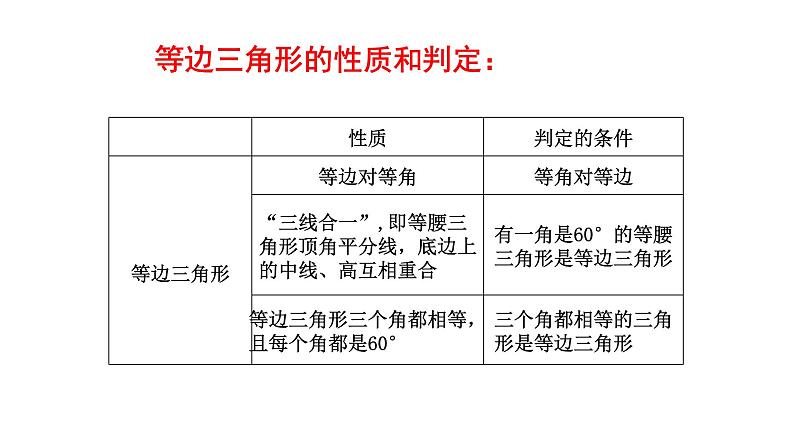
定理1：有一个角是60°.的等腰三角形是等边三角形．
等边三角形的判定定理：
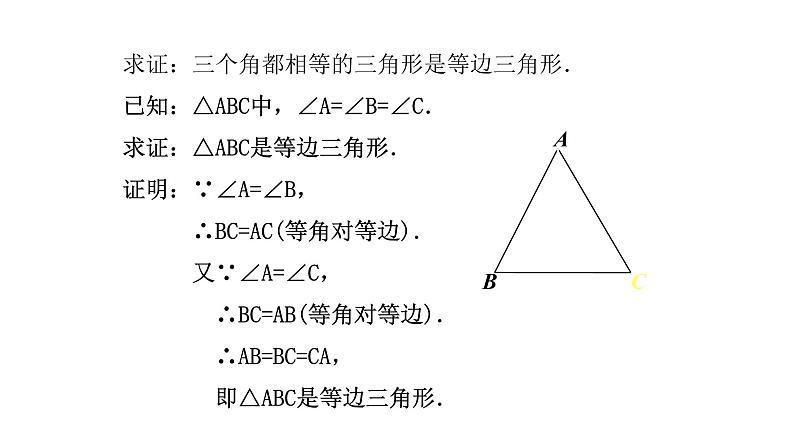
定理2:三个角都相等的三角形是等边三角形
求证：三个角都相等的三角形是等边三角形．已知：△ABC中，∠A=∠B=∠C．求证：△ABC是等边三角形．证明：∵∠A=∠B， ∴BC=AC(等角对等边)． 又∵∠A=∠C， ∴BC=AB(等角对等边)． ∴AB=BC=CA， 即△ABC是等边三角形．
等边三角形的性质和判定：
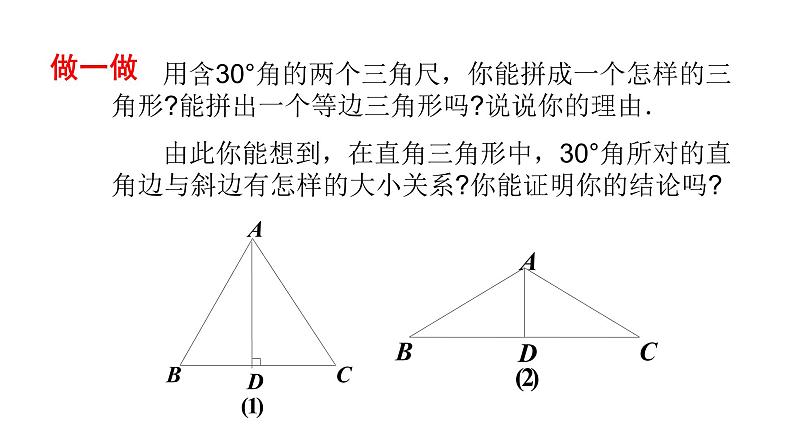
用含30°角的两个三角尺，你能拼成一个怎样的三角形?能拼出一个等边三角形吗?说说你的理由． 由此你能想到，在直角三角形中，30°角所对的直角边与斜边有怎样的大小关系?你能证明你的结论吗?
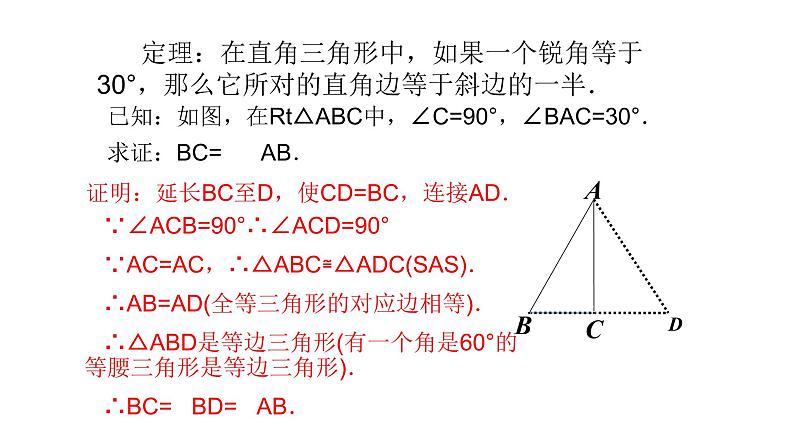
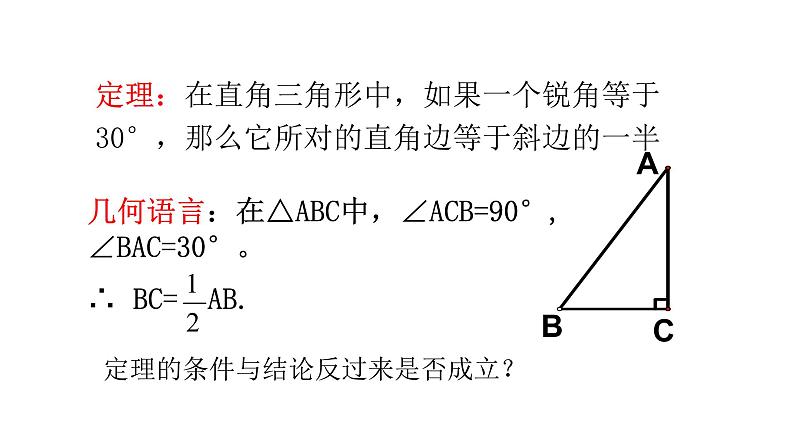
定理：在直角三角形中，如果一个锐角等于30°，那么它所对的直角边等于斜边的一半．
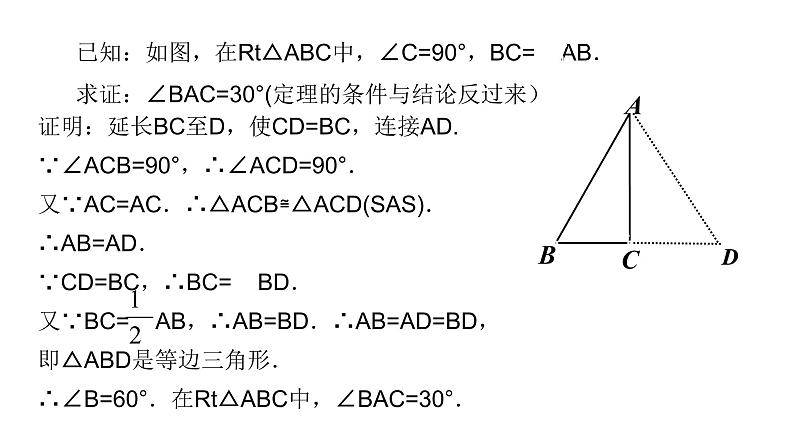
证明：延长BC至D，使CD=BC，连接AD．
定理：在直角三角形中，如果一个锐角等于30°，那么它所对的直角边等于斜边的一半
几何语言：在△ABC中，∠ACB=90°, ∠BAC=30°。∴ BC= AB.
定理的条件与结论反过来是否成立？
证明：延长BC至D，使CD=BC，连接AD.∵∠ACB=90°，∴∠ACD=90°．又∵AC=AC．∴△ACB≌△ACD(SAS)．∴AB=AD．∵CD=BC，∴BC= BD．又∵BC= AB，∴AB=BD．∴AB=AD=BD，即△ABD是等边三角形．∴∠B=60°．在Rt△ABC中，∠BAC=30°．
等腰三角形的底角为15°那么腰上的高是腰长的一半．
已知：如图，在△ABC中，AB=AC=2a，∠ABC=∠ACB=15°,CD是腰AB上的高；求证：CD=a
解：∵　DE⊥AC，BC⊥AC，∠A =30°，
∴　BC =3.7（m）．　
答：立柱BC 的长是3.7 m，DE 的长是1.85 m．　　
　　例2　如图是屋架设计图的一部分，点D 是斜梁AB的中点，立柱BC、DE 垂直于横梁AC，AB =7.4 cm，∠A =30°，立柱BC、DE 要多长？
练习1.如图,在△ABC中,已知AB=AC,∠C=30°,AB⊥AD,AD=4 cm.求: (1)∠DAC的度数; (2)BC的长.
解:(1)∵AB=AC,∠C=30°, ∴∠B=30°. ∴∠BAC=180°-30°-30°=120°. ∵AB⊥AD, ∴∠DAC=120°-90°=30°. (2)∵AD=4 cm,∠B=30°,∠BAD=90°, ∴BD=8 cm. ∵∠DAC=30°=∠C, ∴DC=AD=4 cm. ∴BC=BD+DC=12 cm.
2.如图，AB＝AC，点D是BC的中点，AB平分∠DAE，AE⊥BE，垂足为E.(1)求证：AD＝AE；(2)若BE∥AC，试判断△ABC的形状，并说明理由．
(1)证明：如图，∵AB＝AC，点D是BC的中点，∴AD⊥BC，∴∠ADB＝90°.∵AE⊥BE，∴∠E＝90°＝∠ADB.∵AB平分∠DAE，∴∠1＝∠2，在△ADB和△AEB中，∠ADB=∠E,AB＝AB，∠1=∠2，∴△ADB≌△AEB(AAS)，∴AD＝AE.
(2)解：△ABC是等边三角形．理由如下：∵BE∥AC，∴∠EAC＝90°.∵AB＝AC，点D是BC的中点，∴∠1＝∠2＝∠3＝30°，∴∠BAC＝∠1＋∠3＝60°，∴△ABC是等边三角形．
3．如图，△ABC是等边三角形，D是AB边上一点，以CD为边作等边△CDE，使点E，A在直线DC同侧.连接AE，求证：AE∥BC.证明：∵△ABC，△CDE是等边三角形，∴∠BCD＋∠ACD＝∠ACE＋∠ACD＝60°，∴∠BCD＝∠ACE.在△BCD和△ACE中，BC＝AC，∠BCD＝∠ACE，CD＝CE，∴△BCD≌△ACE(SAS)，∴∠B＝∠CAE.∵∠B＝∠ACB，∴∠CAE＝∠ACB，∴AE∥BC
4．已知，如图所示，P为等边三角形ABC内的一点，它到三边AB，AC，BC的距离分别为h1，h2，h3，△ABC的高AM＝h.则h与h1，h2，h3有何数量关系？写出你的猜想并加以证明．
解：猜想：h1＋h2＋h3＝h.证明如下：连接PA，PB，PC.∵S△PAB＋S△PAC＋S△PBC＝S△ABC，∴ AB·h1＋ AC·h2＋ BC·h3＝ BC·h.∵△ABC是等边三角形，∴AB＝AC＝BC，∴h1＋h2＋h3＝h
提高训练．在四边形ABCD中，AB＝BC＝CD＝DA，∠B＝∠D＝60°，连接AC.(1)如图①，点E，F分别在边BC，CD上，且BE＝CF.求证：①△ABE≌△ACF；②△AEF是等边三角形．(2)若点E在BC的延长线上，在直线CD上是否存在点F，使△AEF是等边三角形？请证明你的结论(图②备用)．
解：(1)证明：①∵AB＝BC，∠B＝60°，∴△ABC是等边三角形，∴AB＝AC.同理，△ADC是等边三角形，∴∠ACF＝∠B＝60°.又∵BE＝CF，∴△ABE≌△ACF.②由△ABE≌△ACF得，AE＝AF，∠BAE＝∠CAF.∵∠BAE＋∠CAE＝60°，∴∠CAF＋∠CAE＝60°，即∠EAF＝60°，∴△AEF是等边三角形　
提高训练．在四边形ABCD中，AB＝BC＝CD＝DA，∠B＝∠D＝60°，连接AC.(2)若点E在BC的延长线上，在直线CD上是否存在点F，使△AEF是等边三角形？请证明你的结论(图②备用)．
(2)存在．证明：如图，在CD的延长线上取点F，使CF＝BE，与(1)①同理可证△ABE≌△ACF，∴∠BAE＝∠CAF，∴∠CAF－∠CAE＝∠BAE－∠CAE，∴∠EAF＝∠BAC＝60°，∴△AEF是等边三角形
1.等边三角形的判定方法:(1)_____________相等的三角形是等边三角形; (2)_____________相等的三角形是等边三角形; (3)_____________的等腰三角形是等边三角形. 2.有一个角为30°的直角三角形的性质定理:在直角三角形中, 如果有一个锐角等于____,那么它所对的_______是______的一半.  
　　有一个角是60° 　　
课外作业1：如图，△ABC为等边三角形，AE＝CD，AD，BE相交于点P，BQ⊥AD于点Q，PQ＝3，PE＝1，求AD的长．
解：根据SAS可证△ABE≌△CAD，∴BE＝AD，∠ABE＝∠CAD.∵∠BPQ＝∠ABE＋∠BAD，∠BAC＝∠CAD＋∠BAD，∴∠BPQ＝∠BAC＝60°，又∵BQ⊥AD，∴∠BQP＝90°，∴∠PBQ＝90°－∠BPQ＝30°，∴PQ＝ BP，∴BP＝2PQ＝2×3＝6，∴BE＝BP＋PE＝7，∴AD＝BE＝7
课外作业2.如图1，已知点P是线段AB上的动点(P不与A，B重合)，分别以AP，PB为边向线段AB的同一侧作等边△APC和等边△PBD.连接AD，BC，相交于点Q，AD交CP于点E，BC交PD于点F.(1)图1中有______对全等三角形；(不必证明)(2)图1中设∠AQC＝α，那么α＝________°；(不必证明)(3)如图2，若点P固定，将△PBD绕点P按顺时针方向旋转(旋转角小于180°)，此时α的大小是否发生变化？请说明理由．
解：(1)△APD≌△CPB，△EPD≌△FPB，△APE≌△CPF，一共有3对(2)∵△APC是等边三角形，∴PA＝PC，∠APC＝60°，∵△BDP是等边三角形，∴PB＝PD，∠BPD＝60°，∴∠APC＝∠BPD，∴∠APD＝∠CPB，在△APD和△CPB中，PA＝PC。∠APD＝∠CPB，PB＝PD
∴△APD≌△CPB(SAS)，∴∠PAD＝∠PCB，∵∠QAP＋∠QAC＋∠ACP＝120°，∴∠QCP＋∠QAC＋∠ACP＝120°，∴∠AQC＝180°－120°＝60°.故答案为60