北师大版九年级下册2 二次函数的图像与性质优秀课件ppt

这是一份北师大版九年级下册2 二次函数的图像与性质优秀课件ppt，共21页。PPT课件主要包含了抛物线，顶点坐标，对称轴，开口方向，增减性，yx2，y-x2，1列表，y2x2，图2-4等内容，欢迎下载使用。

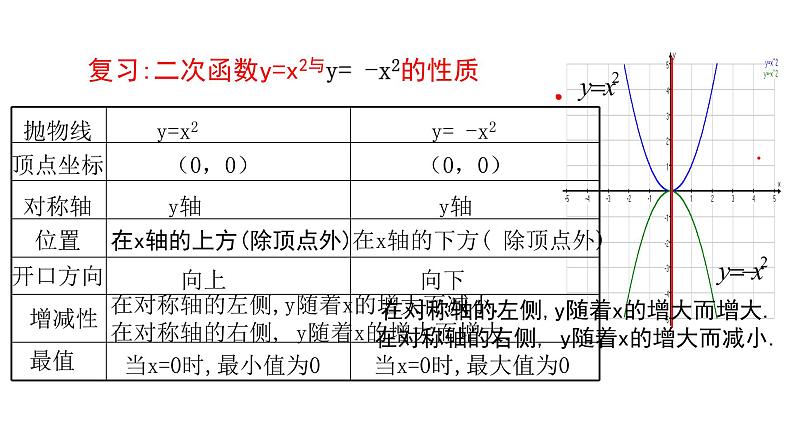
复习:二次函数y=x2与y= -x2的性质
在x轴的上方(除顶点外)
在x轴的下方( 除顶点外)
当x=0时,最小值为0
当x=0时,最大值为0
在对称轴的左侧,y随着x的增大而减小. 在对称轴的右侧, y随着x的增大而增大.
在对称轴的左侧,y随着x的增大而增大. 在对称轴的右侧, y随着x的增大而减小.
下面接着讨论形如y=ax2, y=ax2+c 的二次函数的图象和性质.
画二次函数y=2x2的图象.
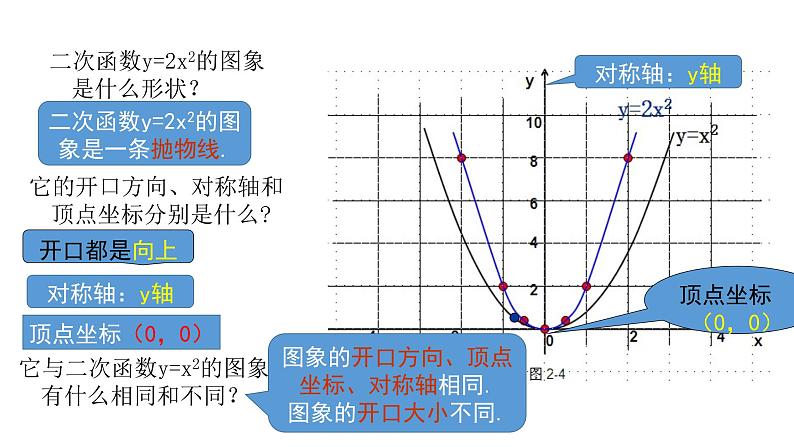
二次函数y=2x2的图象是什么形状？
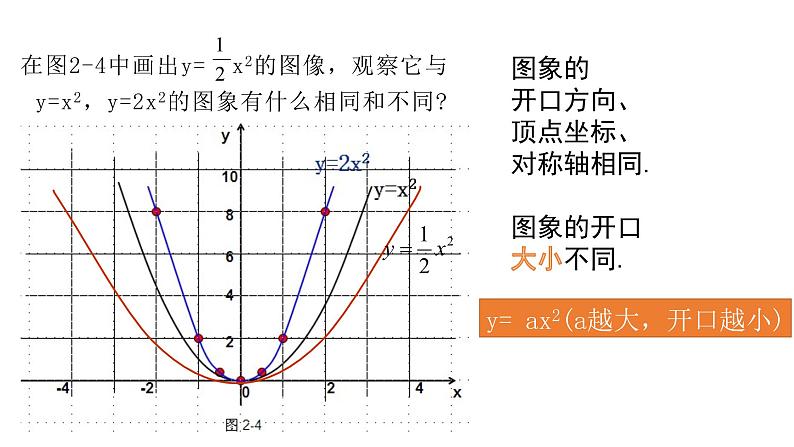
图象的开口方向、顶点坐标、对称轴相同.图象的开口大小不同.
二次函数y=2x2的图象是一条抛物线.
它的开口方向、对称轴和顶点坐标分别是什么?
它与二次函数y=x2的图象有什么相同和不同？
在图2-4中画出y= x2的图像，观察它与y=x2，y=2x2的图象有什么相同和不同?
y= ax2(a越大，开口越小)
画二次函数y=2x2+1的图象，你是怎样画的？与同伴交流.
1列表、2描点、3连线
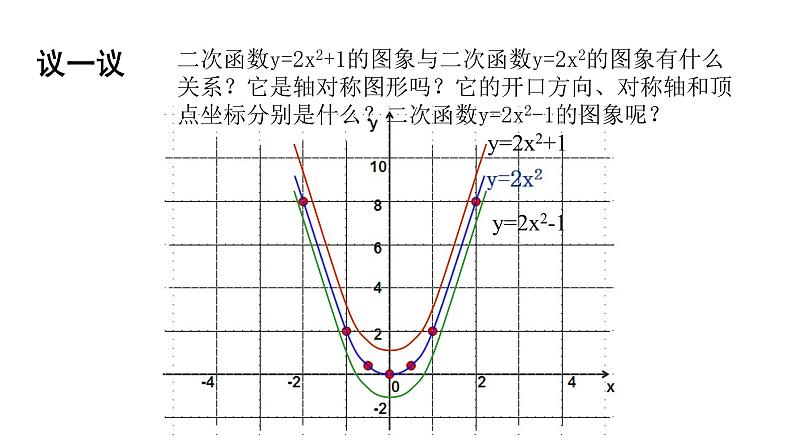
二次函数y=2x2+1的图象与二次函数y=2x2的图象有什么关系？它是轴对称图形吗？它的开口方向、对称轴和顶点坐标分别是什么？二次函数y=2x2-1的图象呢？
将二次函数y=2x2的图象向上平移1个单位，就得到函数y=2x2+1的图象.
将二次函数y=2x2的图象向下平移1个单位，就得到函数y=2x2-1的图象.
你能总结一下二次函数y=2x2、y=2x2+1、 y=2x2+1 （a≠0）的图象和性质吗？
二次函数y=2x2，y=2x2+1，y=2x2-1的图象都是抛物线，并且形状相同，只是位置不同.
顶点坐标与对称轴.位置与开口方向.
y=2x2 y=2x2+1 y=2x2-1
（0，0） （0，1） （0，-1）
y轴(X=0) y轴(X=0) y轴(X=0)
将二次函数y=2x2的图象向上平移一个单位
将二次函数y=2x2的图象向下平移一个单位
向上 向上 向上
二次函数y=ax2与y=ax2+c的图象有什么关系？
二次函数y=ax2+c的图象可以由 y=ax2 的图象(当c > 0 时 ) 向上平移c个单位得到.(当c < 0 时) 向下平移-c个单位得到.
二次函数 的图象与二次函数 的图象有什么关系？它是轴对称图形吗？它的开口方向、对称轴和顶点坐标分别是什么？画图看一看.2. 二次函数 的图象与二次函数 的图象有什么关系？
的图象向上移动0.5个单位,便得y=3x2
都是轴对称图形，开口都向上，对称轴都是x=0，顶点坐标分别是（0，0.5）（0.0）
的图象向下移动1个单位得
3.在同一坐标系中作出y＝－x2，y＝－x2＋3，y＝－x2－3的图象，根据图象填空：抛物线y＝－x2的顶点坐标是 ，对称轴是 ，开口向 ；抛物线y＝－x2＋3的顶点坐标是 ，对称轴是 ，开口向 ；抛物线y＝－x2－3的顶点坐标是 ，对称轴是 ，开口向 ；抛物线y＝－x2＋3，y＝－x2－3与y＝－x2的（ ） 只是抛物线（ ）不同；把抛物线y＝－x2沿y轴向 平移抛物线的顶点位置发生了变化，把抛物线y＝－x2沿y轴向 平移 个单位就可得到抛物线y＝－x2＋3 ； 向 平移 个单位就可得到抛物线y＝－x2－3．
二次函数y=ax2和y=ax2+c的关系
1.相同点：(1)形状相同(图象都是抛物线,开口方向相同). (2)对称轴都是y轴.(3)都有最(大或小)值.(4)a>0时, 开口向上,在对称轴左侧,y都随x的增大而减小,在对称轴右侧,y都随 x的增大而增大. a<0时,开口向下,在对称轴左侧,y都随x的增大而增大,在对称轴右侧,y都随 x的增大而减小 .
2.不同点: (1)位置不同(2)顶点不同:分别是 （0，0） 和（0，c）.(3) 最值不同:分别是0和c.3.联系: y=ax²+c(a≠0) 的图象可以看成y=ax²的图象沿对称轴整体上(下)平移c个单位 (当c>0时向上平移;当c<0时,向下平移)得到的.
1. 若ab＜0，则函数y=ax2和y=ax+b在同一坐标系中的图象大致为（ ）
2.已知二次函数y=ax2的图象如图X2-2-3，则下列哪个选项表示的点有可能在反比例函数y= 的图象上（ ）A．(-1，2)B．(1，-2)C．(2，3)D．(2，-3)
3. 二次函数y=2x2-3的图象是一条抛物线，下列关于该抛物线的说法，正确的是（ ）A. 抛物线开口向下B. 抛物线经过点（2，3）C. 抛物线的对称轴是直线x=1D. 抛物线与x轴有两个交点
4.函数y=4x2+5的图象可由y=4x2-11的图象向________平移________个单位得到.5. 若抛物线y=ax2（a≠0）过点 （-1，3 ）,则a的值是________. 6. 若点A（-1，m）和B（-2，n）在二次函数y=-x2+20的图象上，则m________n（填“>”“<”或“=”）.