初中数学北师大版八年级下册5 一元一次不等式与一次函数公开课ppt课件

这是一份初中数学北师大版八年级下册5 一元一次不等式与一次函数公开课ppt课件，共17页。PPT课件主要包含了CONTENTS，学习目标，新课导入，新课讲解，课堂小结，当堂小练，拓展与延伸，布置作业等内容，欢迎下载使用。
一元一次不等式与一次函数的关系.（重点、难点）
1．一次函数的基本形式是什么？2．一次函数的性质有哪些？
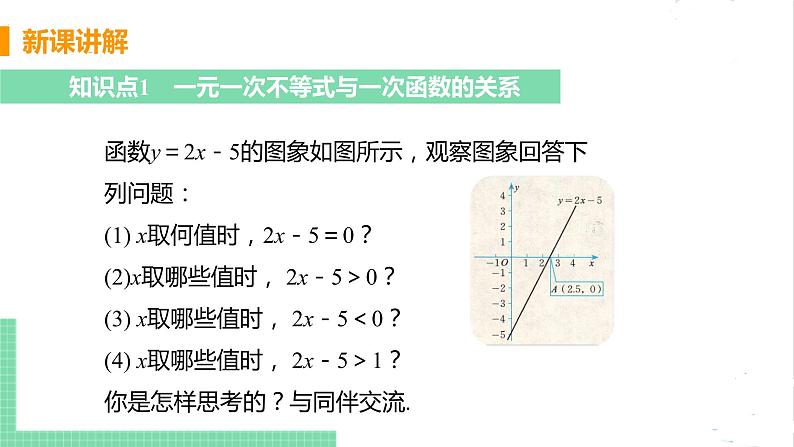
知识点1 一元一次不等式与一次函数的关系
函数y＝2x－5的图象如图所示，观察图象回答下列问题：(1) x取何值时，2x－5＝0？(2)x取哪些值时， 2x－5＞0？(3) x取哪些值时， 2x－5＜0？(4) x取哪些值时， 2x－5＞1？你是怎样思考的？与同伴交流.
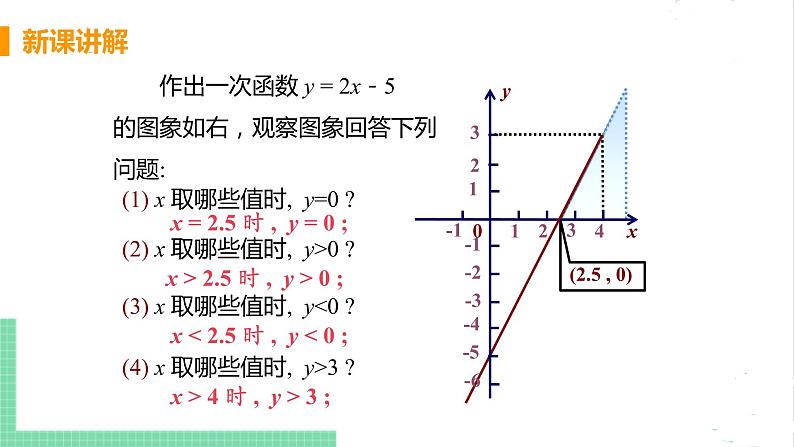
作出一次函数 y = 2x－5 的图象如右，观察图象回答下列问题:
(1) x 取哪些值时, y=0 ?
(2) x 取哪些值时, y>0 ?
x > 2.5 时 , y > 0 ;
x = 2.5 时 , y = 0 ;
(3) x 取哪些值时, y3 ?
x > 4 时 , y > 3 ;
将“一次函数值的问题”改为“一次不等式的问题”
所以，将(1)～(4) 中的 y 换成 2x－5，则，原题“关于一次函数的值的问题”就变成了“关于一次不等式的问题”.
能否把 “关于一次不等式的问题”变换成 “关于一次函数的值的问题”？
1．一次函数和一元一次不等式的联系：任何一个以x为未知数的一元一次不等式都可以变形为ax＋b＞0或ax＋b＜0(a≠0，a，b为常数)的形式，所以解一元一次不等式可以看成是求一次函数y＝ax＋b(a≠0，a，b为常数)的函数值大于0或小于0时，自变量x的取值范围；反映在图象上，就是直线y＝ax＋b在x轴上方的部分或在x轴下方的部分对应的自变量x的取值范围．
直线y＝x－1在x轴上方的点对应的x应满足x－1>0，∴x＞1.∴选A.
对于直线y＝x－1，在x轴上方的点对应的x的取值范围是(　　)A．x＞1　　　　　　B．x≥1　　　C．x＜1　　　　　　D．x≤1
解这类题目的关键是要将比较函数值的大小的问题转化成解不等式的问题．
已知函数y1＝2x－5，y2＝3－2x，求当x取何值时，(1) y1＞y2？ (2) y1＝y2? (3) y1＜y2?
方法一：代数法．(1)y1＞y2，即2x－5＞3－2x，解得x＞2.(2)y1＝y2，即2x－5＝3－2x，解得x＝2.(3)y1＜y2，即2x－5＜3－2x，解得x＜2. 所以当x＞2时，y1＞y2；当x＝2时，y1＝y2； 当x＜2时，y1＜y2.
方法二：图象法．在同一直角坐标系内画出函数y1＝2x－5和y2＝3－2x的图象，如图所示．由图象知，两直线的交点坐标为(2，－1)．观察图象可知，当x＞2时，y1＞y2；当x＝2时，y1＝y2；当x＜2时，y1＜y2.
1.已知y1＝－x＋3，y2＝3x－4，当x取哪些值时?y1＞y2？你是怎样做的？与同伴交流.
当y1＜y2，即－x＋3＜3x－4时，解得x＞ .所以当x＞ 时，y1＜y2.
2.已知y1＝－x＋5，y2＝5x－4.(1)当x________时，y1＝y2；(2)当x________时，y1>y2；(3)当x________时，y1