初中数学北师大版八年级下册3 公式法优秀课件ppt

这是一份初中数学北师大版八年级下册3 公式法优秀课件ppt，共17页。PPT课件主要包含了学习目标，新课导入，新课讲解，课堂小结，当堂小练，拓展与延伸，布置作业，提公因式法，平方差公式，整式乘法等内容，欢迎下载使用。

用平方差公式分解因式 平方差公式在分解因式中的应用.（重点、难点）
1、什么叫把多项式分解因式?
把一个多项式化成几个整式的积的形式，叫做多项式的分解因式.
2、已学过哪一种分解因式的方法?
知识点1 用平方差公式分解因式
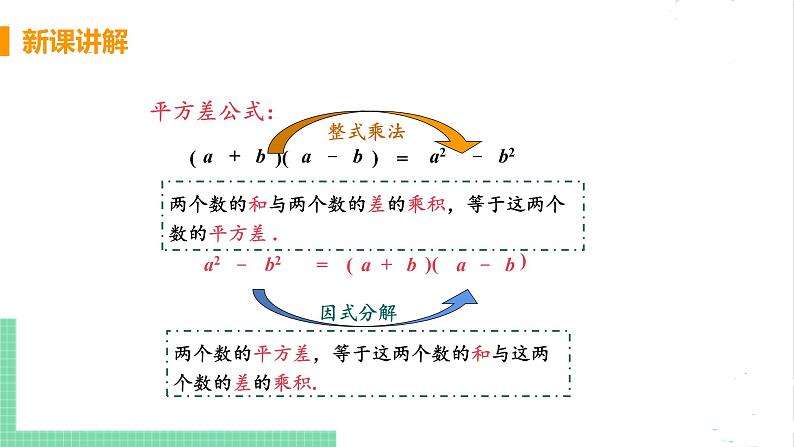
(a+b)(a－b)=a2－b2
这种分解因式的方法称为公式法.
a2－b2= (a+b)(a－b)
两个数的和与两个数的差的乘积，等于这两个数的平方差 .
两个数的平方差，等于这两个数的和与这两个数的差的乘积.
把下列各式因式分解:(1)25－16x2； (2)9a2－ b2.
(1) 25－16x2＝ 52－(4x)2＝(5＋4x)(5－4x)；
(2)9a2－ b2＝ (3a)2－( b)2＝(3a＋ b)(3a－ b)
1.判断正误：(1) x2＋y2＝(x＋y)(x＋y)； ( )(2) x2－y2＝(x＋y)(x－y)； ( )(3) －x2＋y2＝(－x＋y)(－x－y)； ( )(4) －x2－y2＝－(x＋y)(x－y)； ( )
2.把下列各式因式分解：(1) a2b2－m2；(2) (m－a)2－(n＋b)2；(3) x2－(a＋b－c)2；(4) －16x4＋81y4.
(1)a2b2－m2＝(ab＋m)(ab－m)．(2)(m－a)2－(n＋b)2＝[(m－a)＋(n＋b)]·[(m－a) －(n＋b)]＝(m－a＋n＋b)(m－a－n－b)．
(3)x2－(a＋b－c)2＝[x＋(a＋b－c)][x－(a＋b－c)] ＝(x＋a＋b－c)(x－a－b＋c)．(4)方法一：－16x4＋81y4＝－(16x4－81y4) ＝－(4x2＋9y2)(4x2－9y2) ＝－(4x2＋9y2)(2x＋3y)(2x－3y)．方法二：－16x4＋81y4＝81y4－16x4＝(9y2＋4x2) (9y2－4x2)＝(9y2＋4x2)(3y＋2x)(3y－2x)．
知识点2 平方差公式在分解因式中的应用
请你写出几个能用平方差公式因式分解的多项式(每人写两个).
用平方差公式分解因式时，若多项式有公因式，要先提取公因式，再用平方差公式分解因式.
(1) 9(m＋n)2－(m－n)2 ＝[3(m＋n)]2－(m－n)2＝ [3(m＋n)＋(m－n)] [3(m＋n)－(m－n)]＝ (3m＋3n＋m－n)(3m＋3n－m＋n)＝(4m＋2n)(2m＋4n)＝4(2m＋n)(m＋2n); (2)2x3－8x＝2x(x2－4) ＝ 2x(x2－22) ＝2x (x＋2)(x－2)
把下列各式因式分解：(1)9(m＋n)2－(m－n)2； (2) 2x3－8x.
一次课堂练习，小颖同学做了以下几道因式分解题，你认为她做得不够完整的是(　　)A．x3－x＝x(x2－1)B．x2y－y3＝y(x＋y)(x－y)C．－m2＋4n2＝(2n＋m)(2n－m)D．3p2－27q2＝3(p＋3q)(p－3q)
应用平方差公式分解因式的注意事项：(1)等号左边： ①等号左边应是二项式； ②每一项都可以表示成平方的形式； ③两项的符号相反．(2)等号右边是等号左边两底数的和与这两个数的 差的积．
1.如图，从边长为(a＋3)的正方形纸片中剪去一个边长为3的正方形，剩余部分沿虚线又剪拼成一个长方形(不重叠无缝隙)，则拼成的长方形的长是________．
2.n是整数，式子 [1－(－1)n](n2－1)计算的结果(　　)A．是0 B．总是奇数C．总是偶数 D．可能是奇数也可能是偶数