初中数学北师大版八年级下册1 平行四边形的性质优秀课件ppt

这是一份初中数学北师大版八年级下册1 平行四边形的性质优秀课件ppt，共22页。PPT课件主要包含了学习目标，新课导入，新课讲解，课堂小结，当堂小练，拓展与延伸，布置作业，两组对边分别平行，四边形，平行四边形等内容，欢迎下载使用。

平行四边形的定义 平行四边形的对称性 平行四边形的对边的性质平行四边形角的性质（重点、难点）
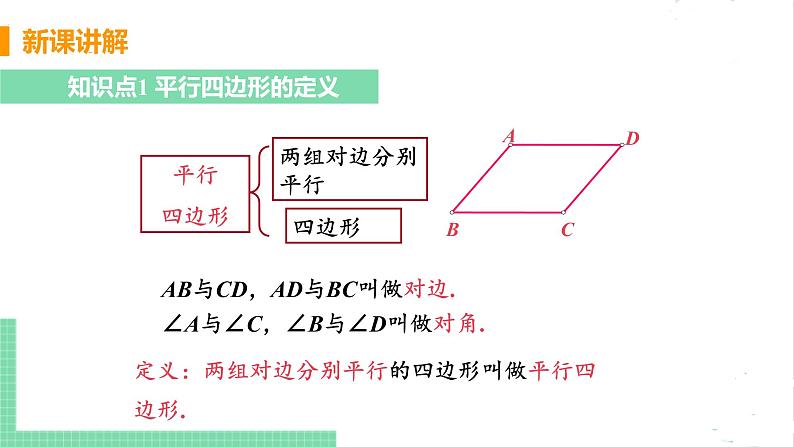
知识点1 平行四边形的定义
∠A与∠C，∠B与∠D叫做对角.
AB与CD，AD与BC叫做对边.
定义：两组对边分别平行的四边形叫做平行四边形.
如图，在 ABCD中，过点P作直线EF，GH分别平行于AB，BC，那么图中共有平行四边形_____个．
根据平行四边形的定义，知AB∥CD，AD∥BC，由已知可知，EF∥AB，GH∥BC，所以根据平行四边形的定义可以判定四边形ABFE是平行四边形，同理可判定四边形EFCD、四边形AGHD、四边形GBCH、四边形AGPE、四边形EPHD、四边形GBFP、四边形PFCH都是平行四边形，最后还要加上 ABCD，即共有9个平行四边形．
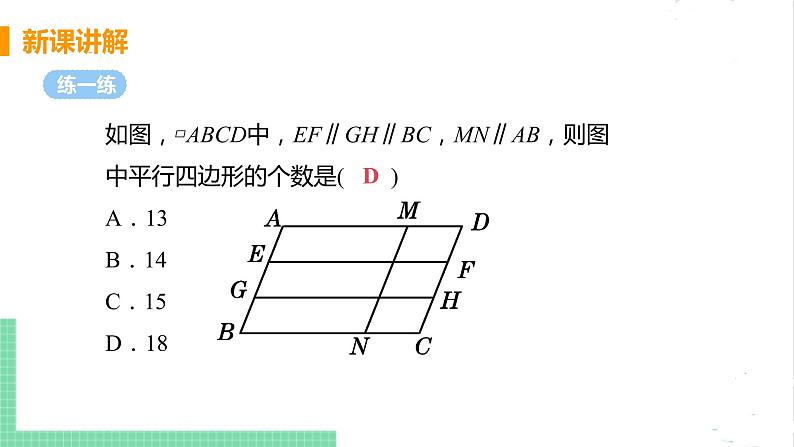
如图，▱ABCD中，EF∥GH∥BC，MN∥AB，则图中平行四边形的个数是(　　)A．13 B．14 C．15 D．18
知识点2 平行四边形的中心对称性
(1)平行四边形是中心对称图形吗？如果是，你能找出它的对称中心并验证你的结论吗？
如图，已知过 ABCD的对角线BD上一点M分别作平行四边形两组对边的平行线EF与GH，则图中 AEMG的面积S1与 HCFM的面积S2的大小关系是(　　)A．S1＞S2　　　　　　　　B．S1＜S2C．S1＝S2 D．2S1＝S2
在平面直角坐标系中，已知▱ABCD的三个顶点坐标分别是A(a，b)，B(4，－2)，C(－a，－b)，则下列关于点D的说法正确的是(　　)甲：点D在第一象限乙：点D与点A关于原点对称丙：点D的坐标是(－4，2)丁：点D到原点距离是2A．甲乙 B．丙丁 C．甲丁 D．乙丙
知识点3 平行四边形的对边的性质
(2)你还发现平行四边形有哪些性质？
我们还发现：平行四边形的对边相等、对角相等.请你尝试证明这些结论.
边的性质：平行四边形对边平行；平行四边形对边相等．数学表达式：如图，∵四边形ABCD是平行四边形，∴AB∥CD，AD∥BC，AB＝CD，AD＝BC.
已知：如图(1)，四边形ABCD是平行四边形.求证：AB＝CD，BC＝DA.
连接AC(如图(2)).∵四边形ABCD是平行四边形，∴ AB∥CD，BC∥DA(平行四边形的定义）.∴∠1＝∠2,∠3＝∠4.∵AC＝CA，∴△ABC≌△CDA.∴AB＝CD，BC＝DA.
已知：如图,在 中，E，F是对角线AC上的两点，并且AE＝CF.求证：BE=DF.
∵四边形ABCD是平行四边形，∴ AB＝CD(平行四边形的对边相等），AB∥CD(平行四边形的定义）.∴∠BAE＝∠DCF.又∵AE＝CF，∴△ABE≌△CDF.∴BE＝DF.
如图，在▱ABCD中，对角线AC的垂直平分线分别交AD，BC于点E，F，连接CE，若△CED的周长为6，则▱ABCD的周长为(　　)A．6 B．12 C．18 D．24
知识点4 平行四边形角的性质
1.角的性质：平行四边形对角相等；平行四边形邻角互补．数学表达式：如图，∵四边形ABCD是平行四边形，∴∠A＝∠C，∠B＝∠D.∴∠A＋∠B＝180°，∠B＋∠C＝180°，∠C＋∠D＝180°，∠A＋∠D＝180°.
如图，在 ABCD中，已知∠A＋∠C＝120°，求平行四边形各角的度数．
由平行四边形的对角相等，得∠A＝∠C，结合已知条件∠A＋∠C＝120°，即可求出∠A和∠C的度数；再根据平行线的性质，进而求出∠B，∠D的度数．
在 ABCD中，∠A＝∠C，∠B＝∠D.∵∠A＋∠C＝120°，∴∠A＝∠C＝60°.∴∠D＝180°－∠A＝180°－60°＝120°.∴∠B＝∠D＝120°.
已知平行四边形一个内角的度数，能确定其他内角的度数吗？说说你的理由.
能确定其他内角的度数．理由：由平行四边形的定义和定理，得平行四边形邻角互补，对角相等，因此只要知道平行四边形一个内角的度数，就可确定其他内角的度数．
1.平行四边形的定义：两组对边分别平行的四边形.2.平行四边形具有中心对称性.3.平行四边形的对角相等.4.平行四边形的对角相等.
在▱ABCD中，∠A＋∠C＝200°，则∠B的度数是(　　)A．100° B．160° C．80° D．60°
如图，在▱ABCD中，CE⊥AB，E为垂足，如果∠A＝120°，则∠BCE的度数是(　　)A．80° B．50° C．40° D．30°