初中第六章 平行四边形2 平行四边形的判定优质课件ppt

这是一份初中第六章 平行四边形2 平行四边形的判定优质课件ppt，共17页。PPT课件主要包含了学习目标，新课导入，新课讲解，课堂小结，当堂小练，拓展与延伸，布置作业等内容，欢迎下载使用。

平行线间的距离平行线间的距离的应用（重点、难点）
1.平行四边形的定义是什么？它有什么作用？2.平行四边形有哪些判断方法？
知识点1 平行线间的距离
在笔直的铁轨上，夹在两根铁轨之间的平行枕木是否一样长？你能说明理由吗？与同伴交流.
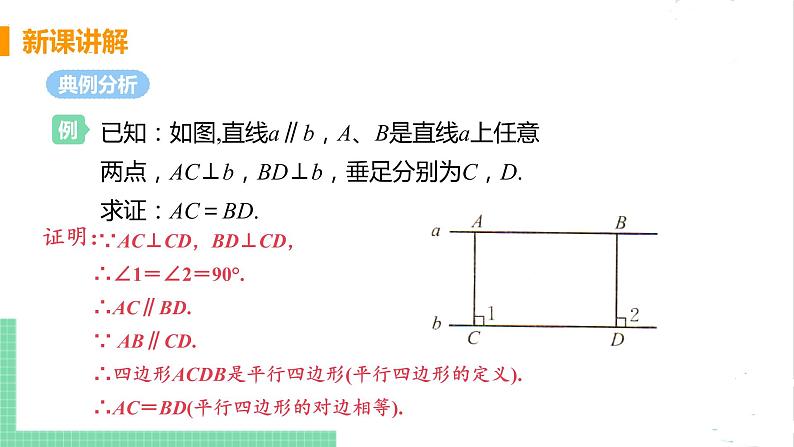
已知：如图,直线a∥b，A、B是直线a上任意两点，AC⊥b，BD⊥b，垂足分别为C，D.求证：AC＝BD.
∵AC⊥CD，BD⊥CD，∴∠1＝∠2＝90°.∴AC∥BD.∵ AB∥CD.∴四边形ACDB是平行四边形(平行四边形的定义).∴AC＝BD(平行四边形的对边相等).
数学表达式：如图，A，C是l1上任意两点，∵l1∥l2，AB⊥l2，CD⊥l2，∴AB＝CD.拓展：(1)夹在两条平行线间的任何平行线段都相等；(2)等底等高的三角形的面积相等．
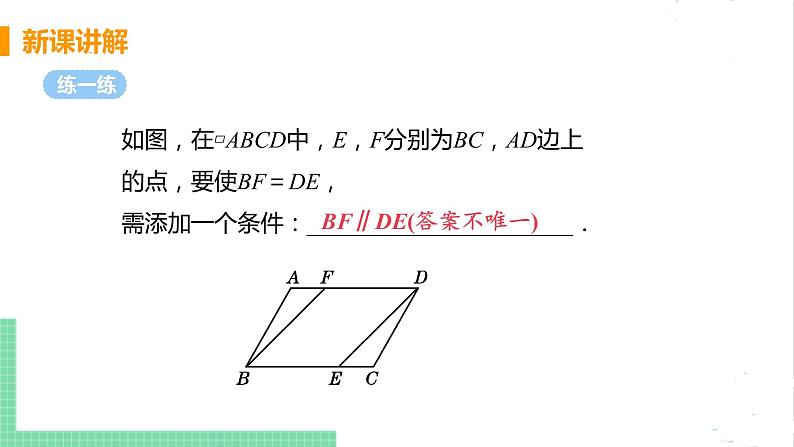
如图，在▱ABCD中，E，F分别为BC，AD边上的点，要使BF＝DE，需添加一个条件：_______________________．
BF∥DE(答案不唯一)
知识点2 平行线间的距离的应用
1.定义：两条平行线中，一条直线上任一点到另一条直线的距离，叫做这两条平行线之间的距离；
2.性质：如果两条直线平行，则其中一条直线上任意两点到另一条直线的距离相等，即：平行线间的距离处处相等．
如图，已知a∥b，AB∥CD，CE⊥b，FG⊥b，点E，G为垂足，则下列结论中错误的是(　　)A．AB＝CD B．CE＝FGC．A，B两点间的距离就是线段AB的长D．直线a，b间的距离就是线段CD的长
根据“两点间的距离”，“两平行线间的距离”的有关概念和定理，可以作出判断．
如图，已知直线a∥b，点A，E，F在直线a上，点B，C，D在直线b上，BC＝EF. △ABC与△DEF的面积相等吗？为什么？
△ABC和△DEF的面积相等．理由如下：如图，作AH1⊥直线b，垂足为点H1，作DH2⊥直线a，垂足为点H2.设△ABC和△DEF的面积分别为S1和S2，∴S1＝ BC·AH1，S2＝ EF·DH2.∵直线a∥b，AH1⊥直线b，DH2⊥直线a，∴AH1＝DH2.又∵BC＝EF，∴S1＝S2，即△ABC与△DEF的面积相等．
如图，a∥b，则直线a与直线b的距离是(　　)A．13 B．14 C．17 D．25
1. 平行线间的距离：两条平行线中，一条直线上任一 点到另一条直线的距离，叫做这两条平行线之间的 距离；2. 平行线间的距离的性质：如果两条直线平行，则其 中一条直线上任意两点到另一条直线的距离相等， 即：平行线间的距离处处相等．
如图，已知l1∥l2，AB∥CD，HE⊥l2，FG⊥l2，垂足分别为E，G，则下列说法错误的是(　　)A．AB的长就是l1与l2之间的距离B．AB＝CDC．HE的长就是l1与l2之间的距离D．HE＝FG
如图，已知直线a∥b，点A，B，C在直线a上，点D，E，F在直线b上，AB＝EF＝2，若△CEF的面积为5，则△ABD的面积为(　　)A．2 B．4 C．5 D．10