北师大版八年级下册2 平行四边形的判定优质ppt课件

这是一份北师大版八年级下册2 平行四边形的判定优质ppt课件，共22页。PPT课件主要包含了学习目标，新课导入，新课讲解，课堂小结，当堂小练，拓展与延伸，布置作业等内容，欢迎下载使用。

由对角线的关系判定平行四边形 平行四边形判定方法的综合应用（重点、难点）
平行四边形的判定方法有哪些？
知识点1 由对角线的关系判定平行四边形
前面我们已经得到了平行四边形的两个判定方法，你还能找到其他的判定方法吗？
你同意他的想法吗？你能证明他的猜想吗？请你试一试.
如图，将两根木条AC，BD的中点重叠，并用钉子固定，四边形ABCD看起来是平行四边形. 于是我猜想：对角线互相平分的四边形是平行四边形.
已知：如图，四边形ABCD的两条对角线AC与BD相交于点O, 并且OA＝OC，OB＝OD.求证：四边形ABCD是平行四边形.
∵OA＝OC，OD＝OB，∠AOD＝∠COB.∴△AOD≌△COB.∴AD＝CB，∠ADO＝∠CBO.∴AD∥CB.∴四边形ABCD是平行四边形(一组对边平行且相等的四边形是平行 四边形).
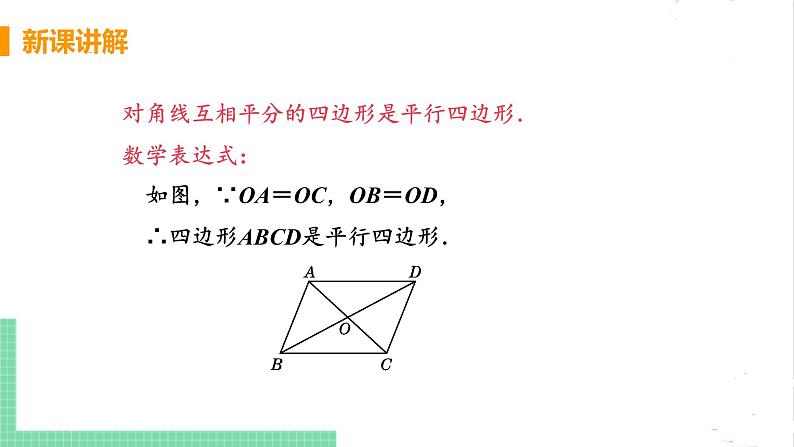
对角线互相平分的四边形是平行四边形．数学表达式：如图，∵OA＝OC，OB＝OD，∴四边形ABCD是平行四边形．
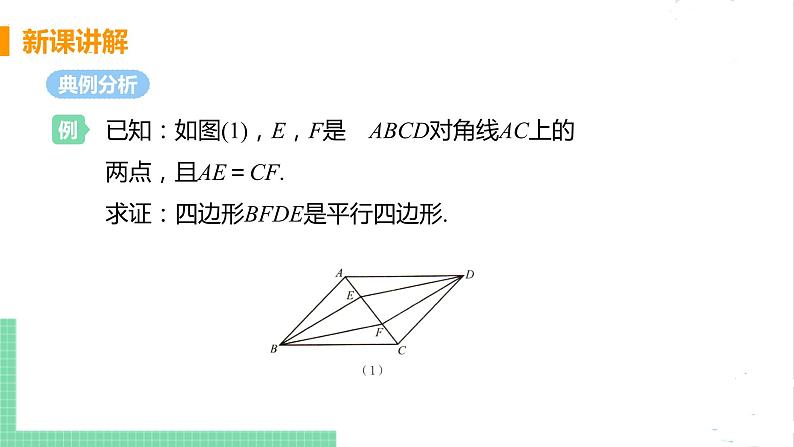
已知：如图(1)，E，F是 ABCD对角线AC上的两点，且AE＝CF. 求证：四边形BFDE是平行四边形.
如图(2)，连接BD，交AC于点O.∵四边形ABCD是平行四边形，∴OA＝OC，OB＝OD(平行四边形的对角线互相平分).∵AE＝CF，∴OA－AE＝OC－CF，即OE＝OF.∴四边形BFDE是平行四边形(对角线互相平分的四边形是平行四边形）.
如图，在 ABCD中，对角线AC与BD相交于点O，点E，F分别是OA和OC的 中点，四边形BFDE是平行四边形吗？请说明理由.
四边形BFDE是平行四边形，理由：∵四边形ABCD是平行四边形，∴OB＝OD，OA＝OC.又∵E，F分别是OA和OC的中点，∴OE＝OF. ∴四边形BFDE是平行四边形．
知识点2 平行四边形判定方法的综合应用
平行四边形的判定方法：(1)定义：两组对边分别平行的四边形是平行四边形.(2)两组对边分别相等的四边形是平行四边形.(3)一组对边平行且相等的四边形是平行四边形.(4)两组对角分别相等的四边形是平行四边形.(5)对角线互相平分的四边形是平行四边形.
如图，四边形ABCD是平行四边形，E，F为对角线AC上两点，连接ED，EB，FD，FB.给出以下结论：①BE∥DF；②BE＝DF；③AE＝CF.请你从中选取一个条件，使∠1＝∠2成立，并给出证明．
欲证明∠1＝∠2，只需证得四边形EDFB是平行四边形或△ABF≌△CDE即可．
(1)补充条件①BE∥DF.证明：∵BE∥DF，∴∠BEC＝∠DFA. ∴∠BEA＝∠DFC.∵四边形ABCD是平行四边形，∴AB＝CD，AB∥CD. ∴∠BAE＝∠DCF.在△ABE与△CDF中，∴△ABE≌△CDF(AAS)．∴BE＝DF. ∴四边形BFDE是平行四边形．∴ED∥BF. ∴∠1＝∠2.
(2)补充条件③AE＝CF.证明：∵AE＝CF，∴AF＝CE.∵四边形ABCD是平行四边形，∴AB＝CD，AB∥CD.∴∠BAF＝∠DCE.在△ABF与△CDE中，∴△ABF≌△CDE(SAS)．∴∠1＝∠2.
如图，在 ABCD中，∠ABC＝70°，∠ABC的平分线交AD于点E，过点D作BE的平行线交BC于点F，求∠CDF的度数.
∵四边形ABCD是平行四边形，∴AD∥BC，∠ABC＝∠ADC.∴ED∥BF. 又∵BE∥DF，∴四边形BEDF是平行四边形．∴∠EBF＝∠FDE.∵∠ABC＝70°，BE平分∠ABC，∴∠EBF＝ ∠ABC＝35°.∴∠FDE＝35°.∵∠ABC＝∠ADC，∴∠CDF＝∠ADC－∠FDE＝35°.
平行四边形的判定方法:(1)定义：两组对边分别平行的四边形是平行四边形．(2)两组对边分别相等的四边形是平行四边形．(3)对角线互相平分的四边形是平行四边形．(4)两组对角分别相等的四边形是平行四边形．(5)一组对边平行且相等的四边形是平行四边形．
　下列说法错误的是(　　)A．对角线互相平分的四边形是平行四边形B．两组对边分别相等的四边形是平行四边形C．一组对边平行且相等的四边形是平行四边形D．一组对边相等，另一组对边平行的四边形是平行四边形
如图，四边形ABCD的对角线相交于点O，AO＝CO，请添加一个条件_______________________(只添一个即可)，使四边形ABCD是平行四边形．
BO＝DO(答案不唯一)
如图，在▱ABCD中，对角线AC，BD相交于O，E，F是对角线AC上的两点，给出下列4个条件：①OE＝OF；②DE＝BF；③∠ADE＝∠CBF；④∠ABE＝∠CDF.其中不能判定四边形DEBF是平行四边形的有(　　)A．0个 B．1个C．2个 D．3个
给出条件①OE＝OF，由四边形ABCD是平行四边形，可得OD＝OB.又∵OE＝OF，∴四边形DEBF为平行四边形．故③正确．故①正确．故③正确．给出条件③∠ADE＝∠CBF，∵四边形ABCD是平行四边形，∴AD＝CB，AD∥CB.∴∠DAE＝∠BCF.又∵∠ADE＝∠CBF，∴△ADE≌△CBF.∴DE＝BF，∠AED＝∠CFB.