数学八年级下册3 三角形的中位线一等奖ppt课件

这是一份数学八年级下册3 三角形的中位线一等奖ppt课件，共20页。PPT课件主要包含了学习目标，新课导入，新课讲解，课堂小结，当堂小练，拓展与延伸，布置作业，平行四边形的判定，对角线等内容，欢迎下载使用。

三角形中位线的性质 三角形中位线在四边形中的应用（重点、难点）
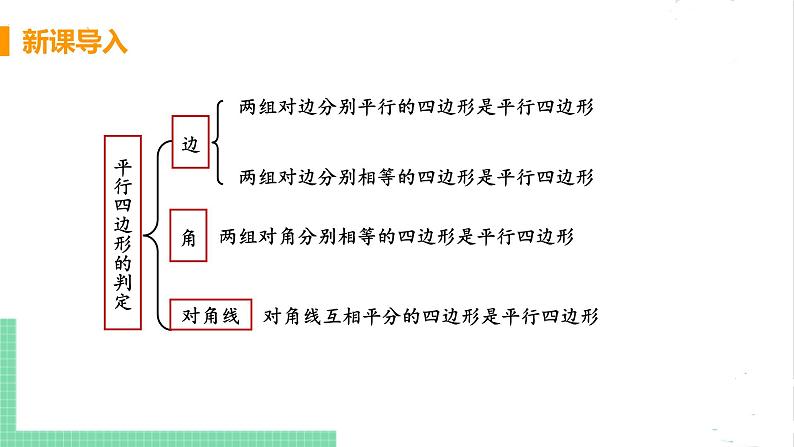
两组对边分别平行的四边形是平行四边形
两组对边分别相等的四边形是平行四边形
两组对角分别相等的四边形是平行四边形
对角线互相平分的四边形是平行四边形
知识点1 三角形中位线的性质
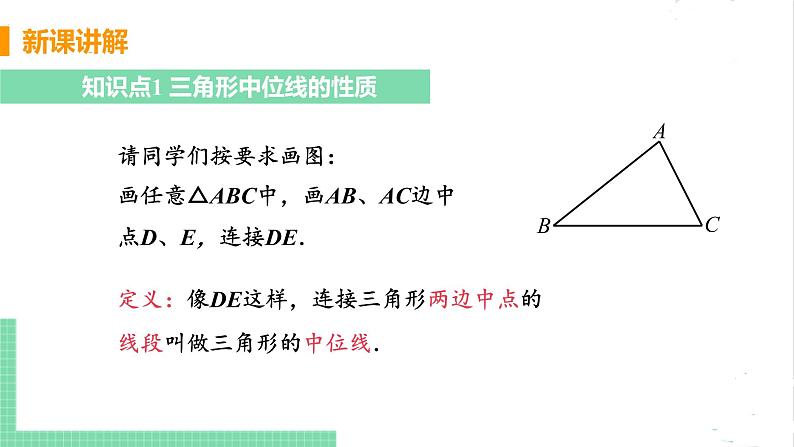
请同学们按要求画图：画任意△ABC中，画AB、AC边中点D、E，连接DE．
定义：像DE这样，连接三角形两边中点的线段叫做三角形的中位线．
如图(2)，延长DE到F，使FE＝DE，连接CF.在△ADE和△CFE中，∵AE＝CE，∠1＝∠2，DE＝FE,∴△ADE≌△CFE.∴∠A＝∠ECF，AD＝CF.
已知：如图(1)，DE是△ABC的中位线.求证：DE∥BC，DE＝ BC.
∴CF∥AB.∵BD＝AD，∴CF＝BD.∴四边形DBCF是平行四边形(一组对边平行且相等的四边形是平行四边形).∴ DF∥BC(平行四边形的定义)，DF＝BC(平行四边形的对边相等).∴DE∥BC，DE＝ BC.
如图，已知E为平行四边形ABCD中DC边延长线上一点，且CE＝DC，连接AE，分别交BC，BD于点F，G，连接AC交BD于点O，连接OF.求证：AB＝2OF.
点O是平行四边形两条对角线的交点，所以点O是线段AC的中点，要证明AB＝2OF，我们只需证明点F是线段BC的中点，即证明OF是△ABC的中位线．
∵四边形ABCD为平行四边形，∴AB∥CD，AB＝CD.∵E为平行四边形ABCD中DC边延长线上一点，且CE＝DC，∴AB∥CE，AB＝CE.∴四边形ABEC是平行四边形．∴点F是BC的中点．又∵点O是AC的中点，∴OF是△ABC的中位线．∴AB＝2OF.
已知三角形的各边长分别为8 cm，10 cm和12 cm，求以各边中点为顶点的三角形的周长.
以各边中点为顶点的三角形的周长为 (8＋10＋12)＝15(cm)．
知识点2 三角形中位线在四边形中的应用
如图，任意画一个四边形，以四边的中点为顶点组成一个新四边形，这个新四边形的形状有什么特征？请证明你的结论，并与同伴交流.
中点四边形的定义：依次连接任意四边形各边中点所得到的四边形称为中点四边形．拓展：不管四边形的形状怎样改变，中点四边形始终是平行四边形．
如图，在四边形ABCD中，点E，F，G，H分别是边AB，BC，CD，DA的中点，连接EF，FG，GH，HE，得到四边形EFGH，求证：四边形EFGH是平行四边形．
如图，连接BD.∵点E，H分别是边AB，DA的中点，∴EH为△ABD的中位线．∴EH∥BD，EH＝ BD.同理可得：FG∥BD，FG＝ BD.∴EH∥FG，EH＝FG.∴四边形EFGH是平行四边形．
如图，已知E，F，G，H分别为四边形ABCD各边的中点，若AC＝10 cm，BD＝12 cm，则四边形EFGH的周长为(　　)A．10 cm B．11 cm C．12 cm D．22 cm
三角形的中位线平行于三角形的第三边，且等于第三边的一半．几何语言(如图)：∵DE是△ABC的中位线，∴DE∥BC．DE= BC．
如图，在▱ABCD中，对角线AC，BD相交于点O，点E是AB的中点，OE＝5 cm，则AD的长为______cm.
如图，四边形ABCD中，∠A＝90°，AB＝3 ，AD＝3，点M，N分别为线段BC，AB上的动点(含端点，但点M不与点B重合)，点E，F分别为DM，MN的中点，则EF长度的最大值为________．
如图，▱ABCD的对角线AC，BD相交于点O，点E，F分别是线段AO，BO的中点，若AC＋BD＝24 cm，△OAB的周长是18 cm，则EF＝________cm.