数学八年级下册18.2.2 菱形优秀ppt课件

这是一份数学八年级下册18.2.2 菱形优秀ppt课件，共25页。PPT课件主要包含了从生活中认识菱形，菱形的四条边相等，知识归纳等内容，欢迎下载使用。
1.能说出菱形的定义和性质. 2.能运用菱形的性质定理进行简单的计算与证明.
重点：菱形的性质. 难点：菱形性质的运用.
追问：你能画出一个菱形吗？
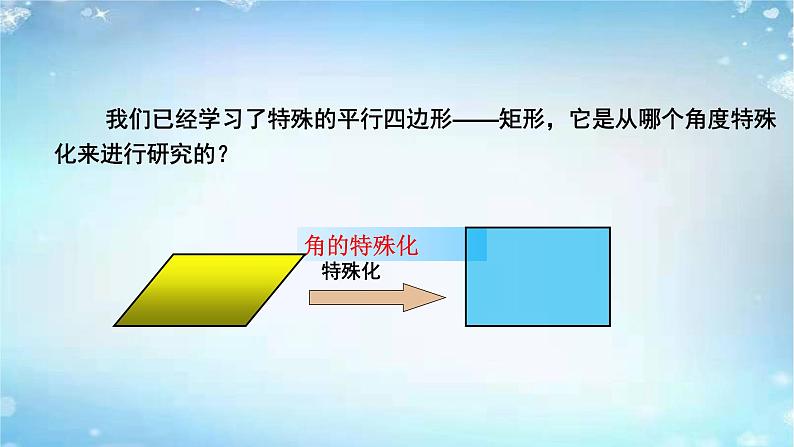
我们已经学习了特殊的平行四边形——矩形，它是从哪个角度特殊化来进行研究的？
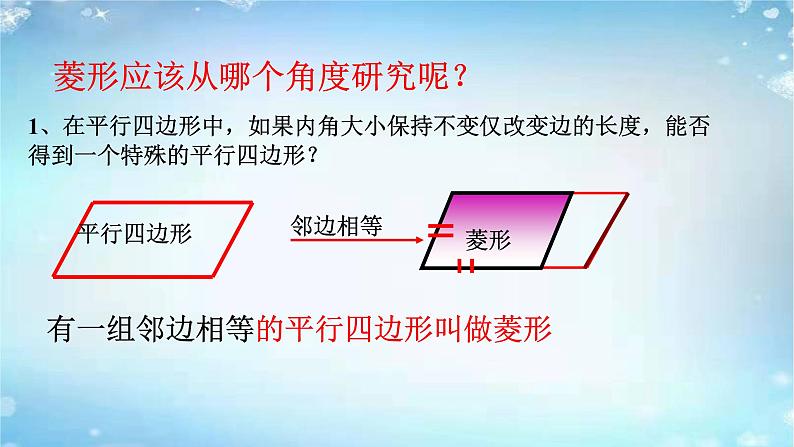
1、在平行四边形中，如果内角大小保持不变仅改变边的长度，能否得到一个特殊的平行四边形？
菱形应该从哪个角度研究呢？
将一张长方形的纸对折、再对折，然后沿图中的虚线剪下，打开即可得到一个菱形.
从折纸中可以得到菱形什么特征？
画出菱形的两条折痕,并通过折叠手中的图形回答以下问题：
１、菱形是轴对称图形吗？
2、菱形有几条对称轴？
3、对称轴之间有什么关系？
4、你能看出图中哪些线段和角相等？
AB=CD=AD=BC OA=OC OB=OD
∠DAB=∠BCD ∠ABC =∠CDA ∠AOB=∠DOC=∠AOD=∠BOC =90° ∠1=∠2=∠3=∠4 ∠5=∠6=∠7=∠8
△ABC △ DBC △ACD △ABD
Rt△AOB Rt△BOC Rt△COD Rt△DOA
Rt△AOB ≌ Rt△BOC≌ Rt△COD ≌ Rt△DOA△ABD≌△BCD △ABC≌△ACD
2.菱形的两条对角线互相垂直，并且每一条对角线平分一组对角。
3.菱形是轴对称图形，也是中心对称图形
求证:菱形的四条边相等 菱形的两条对角线互相垂直， 并且每一条对角线平分一组对角。
已知:如图四边形ABCD是菱形
(1)AB=BC=CD=DA
(2)AC⊥BD
AC平分∠DAB和∠DCB
BD平分∠ADC和∠ABC
证明(1)∵四边形ABCD是菱形
∴DA=DC(菱形的定义)
∵DA=BC,AB=DC
∴AB=BC=DC=DA
(2)在△DAC中,又∵AO=CO
∴DB⊥AC，DB平分∠ADC（三线合一）
同理： DB平分∠ABC； AC平分∠DAB和∠DCB
菱形具有平行四边形的一切性质；
菱形的两条对角线互相垂直，并且每一条对角线平分一组对角；
你能由两条对角线的长度求出它的面积吗？
∵Rt△AOB≌Rt△BOC≌Rt△COD≌Rt△DOA
1.若菱形的边长等于一条对角线的长，则它的一组邻角的度数分别为____________.
2．如图，菱形ABCD的对角线AC，BD的长分别为6，8，则这个菱形的周长为(　　)A．20 B．24 C．40 D．48
3.菱形不具备的性质是(　　) A．四条边都相等 B．对角线一定相等 C．是轴对称图形 D．是中心对称图形
4. 四边形ABCD是菱形，对角线AC、BD相交于点O，且AB=5，AO=4. 求AC和BD的长.
解:∵四边形ABCD是菱形, ∴OA=OC，OB=OD, AC⊥BD. ∵Rt△AOB中,OB2+OA2=AB2, AB=5cm，AO=4cm,
∴OB=3cm. ∴BD=2OB=6cm, AC=2OA=8cm.
5.菱形ABCD的两条对角线BD、AC长分别是6cm和8cm，求菱形的周长和面积.
　6　如图，菱形花坛ABCD的边长为20 m，∠ABC=60°，沿着菱形的对角线修建了两条小路AC和BD．求两条小路的长（结果保留小数点后两位）和花坛的面积（结果保留小数点后一位）．
：有一组邻边相等的平行四边形叫菱形
：S菱形=底×高 S菱形= 对角线乘积的一半
：特在“边、对角线、对称性”