初中数学人教版八年级下册18.1.2 平行四边形的判定获奖课件ppt

这是一份初中数学人教版八年级下册18.1.2 平行四边形的判定获奖课件ppt，共24页。PPT课件主要包含了新课导入，平行四边形研究三角形，动手思考探索，证明猜想，三角形中位线定理，几何语言，随堂演练，能力提升等内容，欢迎下载使用。

1.知道什么是三角形的中位线. 2.知道三角形中位线的性质.
重点：三角形的中位线及其性质. 难点：三角形中位线性质的运用.
　　我们在研究平行四边形时，经常采用把平行四边形转化为三角形的问题，反过来，能否用 呢？
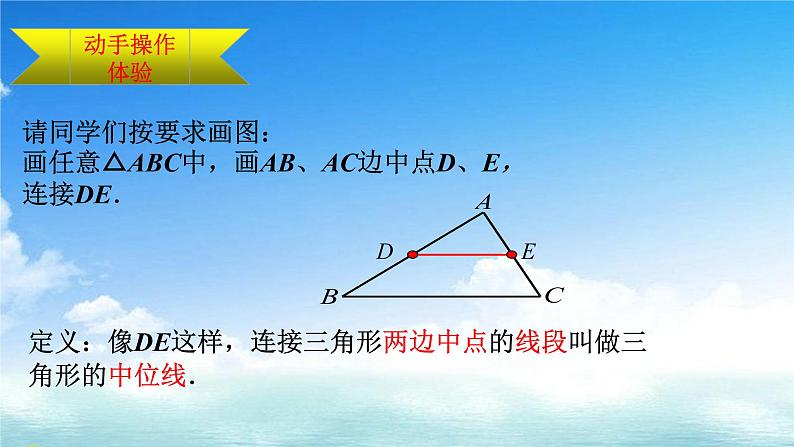
请同学们按要求画图：画任意△ABC中，画AB、AC边中点D、E，连接DE．
定义：像DE这样，连接三角形两边中点的线段叫做三角形的中位线．
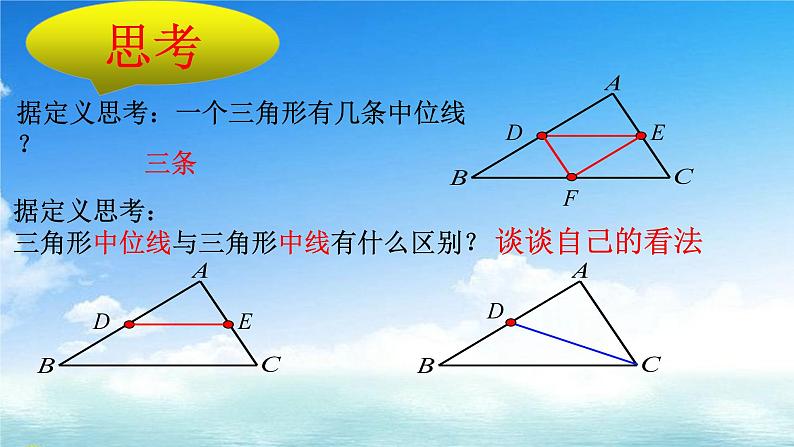
据定义思考：一个三角形有几条中位线？
据定义思考：三角形中位线与三角形中线有什么区别？
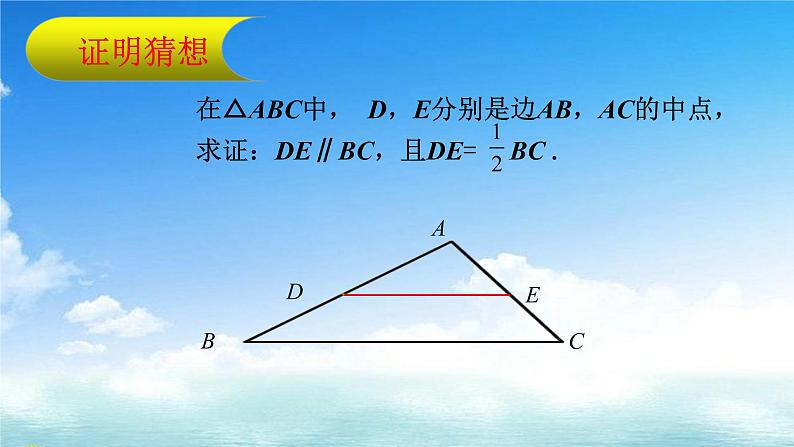
　　看一看，量一量，猜一猜：　　DE与BC之间有什么位置关系和数量关系？
　　猜想：三角形的中位线平行于三角形的第三边，并且等于第三边的一半．
证明：如图，延长DE到点F，使EF=DE，连接FC，DC，AF. ∵AE=EC，DE=EF， ∴四边形ADCF是平行四边形， CF DA. ∴CF BD. ∴四边形DBCF是平行四边形， DF BC. 又 DE= DF, ∴DE ∥BC，且DE= BC.
延长DE到F，使EF=DE．
∴四边形BCFD是平行四边形．
∴△ADE≌△CFE．
∵∠AED=∠CEF，AE=CE，
∴ DE∥BC， ．
三角形的中位线平行于三角形的第三边且等于第三边的一半．
1.如图，点D，E，F分别是△ABC三边的中点，若AB=10cm，AC=8cm，BC=12cm，则EF=____，DF=____，DE=____，△DEF的周长为______ .
　　2.如图，在△ABC中，∠C=90°，AC=8，CB=6，D，E，F分别是BC，AC，AB的中点，则四边形AEDF的周长为________；Rt△ABC的中位线分别是___________；斜边上的中线是_______，其长为______.
3. 如图，A、B两点被池塘隔开，在AB外选一点C，连接AC和BC，怎样量出A、B两点间的距离？根据是什么？
根据是三角形中位线定理．
分别画出AC、BC中点M、N，量出M、N两点间距离，则AB=2MN.
4.如果四边形ABCD是平行四边形，AB=6，且AB的长是 ABCD周长的 ，那么BC的长是多少？
5.已知：如图，点D，E，F分别是△ABC三边上的中点.求证：AD与EF互相平分.(提示：连接ED，FD，先证四边形AEDF是平行四边形）
证明：如图，连接ED、FD, ∵E、D分别为△ABC的中点，
∴ED= AC，ED∥AC，即ED∥AF.
又∵F为AC的中点， ∴ED=AF. ∴四边形AEDF为平行四边形， ∴AD与EF互相平分.
6.如图，▱ABCD的周长为36，对角线AC，BD相交于点O，点E是CD的中点，BD=12，求△DOE的周长．
解：∵▱ABCD的周长为36，∴BC+CD=18．∵点E是CD的中点，∴OE是△BCD的中位线，DE= CD，∴OE= BC，∴△DOE的周长为OD+OE+DE= （BD+BC+CD）=15，即△DOE的周长为15．
7.如图，在△ABC中，点D在BC上，且DC＝AC，CE⊥AD于点E，点F是AB的中点。 求证：EF∥BC.
证明：∵DC＝AC，且CE⊥AD于点E， ∴AE＝ED。 又∵点F是AB的中点， ∴AF＝FB， ∴EF是△ABD的中位线。 ∴EF∥BC。
8. 如图，在△ABC中，BD、CE分别是AC、AB上的中线，BD与CE相交于点O，试探究BO与OD的大小关系.(提示：分别取OB、OC的中点M、N)
如图，取OB、OC的中点M、N，连接EM、MN、ND.∵E、D分别为△ABC的中点，
∴ED∥BC，ED= BC,∵M、N是△OBC的中点，∴MN∥BC，MN= BC
∴ED∥MN，ED=MN.∴四边形EDNM是平行四边形.∴OD=OM=BM.∴OB=2OD.