数学八年级下册18.1.1 平行四边形的性质优质课件ppt

这是一份数学八年级下册18.1.1 平行四边形的性质优质课件ppt，共15页。PPT课件主要包含了教学目标，教学重难点，教学设计，互相平分，活动4例题与练习，根据勾股定理得，又∵OAOC，∴OE＝OF等内容，欢迎下载使用。

1．掌握平行四边形对角线互相平分的性质．2．能综合运用平行四边形对角线的性质解决有关平行四边形的计算问题和简单的证明题．
平行四边形对角线的性质．
平行四边形对角线性质的运用．
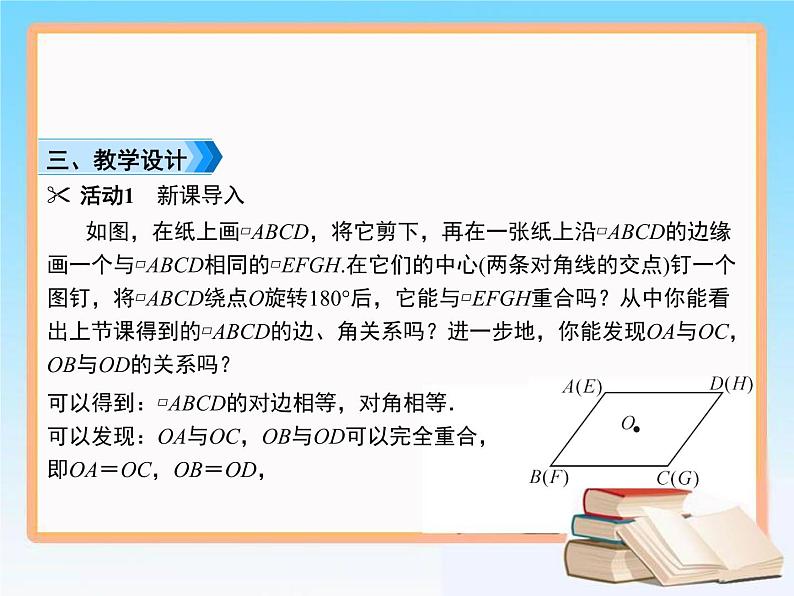
活动1 新课导入
如图，在纸上画▱ABCD，将它剪下，再在一张纸上沿▱ABCD的边缘画一个与▱ABCD相同的▱EFGH.在它们的中心(两条对角线的交点)钉一个图钉，将▱ABCD绕点O旋转180°后，它能与▱EFGH重合吗？从中你能看出上节课得到的▱ABCD的边、角关系吗？进一步地，你能发现OA与OC，OB与OD的关系吗？
可以得到：▱ABCD的对边相等，对角相等．可以发现：OA与OC，OB与OD可以完全重合，即OA＝OC，OB＝OD，
活动2 探究新知
教材P43探究．提出问题：(1)什么叫做平行四边形的对角线？(2)如图，在▱ABCD中，可以通过证明哪两个三角形全等，从而得到OA＝OC，OB＝OD，请写出证明过程；
(3)平行四边形的对角线具有什么性质？(4)△ABC，△DBC，△CAD，△BAD的面积与▱ABCD的面积有怎样的数量关系？为什么？(5)△AOD，△ABO，△BCO，△CDO与▱ABCD的面积有怎样的数量关系？
活动3 知识归纳
1．平行四边形对角线的性质：平行四边形的对角线____________．2．平行四边形的面积＝底×_________．3．平行四边形的两条对角线分成的四个三角形的面积_________，每个三角形的面积是平行四边形面积的______．
解：∵四边形ABCD是平行四边形，
∴BC=AD=8,CD=AB=10.
如图，在 ABCD中，AB=10，AD=8，AC⊥BC. 求BC，CD，AC，OA的长，以及　 ABCD的面积．
例1　教材P44例2.
例2　如图，已知▱ABCD和▱EBFD的顶点A，E，F，C在同一条直线上．求证：AE＝CF.
证明：连接BD交AC于点O.∵四边形ABCD，EBFD是平行四边形，∴OA＝OC，OE＝OF，∴OA－OE＝OC－OF，即AE＝CF.
例3　如图①，在▱ABCD中，O为对角线BD，AC的交点．(1)求证：S△ABO＝S△CBO；(2)如图②，设P为对角线BD上任意一点(点P与点B，D不重合)，S△ABP与S△CBP仍然相等吗？若相等，请证明；若不相等，请说明理由．
解：(1)∵四边形ABCD是平行四边形，
∴AO＝CO.设点B到AC的距离为h，
∴S△ABO＝S△CBO；
(2)S△ABP＝S△CBP.理由如下：在▱ABCD中，点A，C到BD的距离相等，设为h′，
∴S△ABP＝S△CBP.
1．教材P44练习第1，2题．
2．如图，在▱ABCD中，∠ODA＝90°，AC＝10 cm，BD＝6 cm，则AD的长为(　 　)A．4 cm B．5 cm C．6 cm D．8 cm
3．如图，在▱ABCD中，AC，BD为对角线，BC＝6，BC边上的高为4，则阴影部分的面积为(　 　)A．3 B．6 C．12 D．24
4．如图，在▱ABCD中，AC和BD相交于点O，OE⊥AD，OF⊥BC，垂足分别是E，F.求证：OE＝OF.
证明：∵四边形ABCD是平行四边形，∴OB＝OD，AD∥BC，∴∠ODE＝∠OBF.∵OE⊥AD，OF⊥BC，∴∠DEO＝∠BFO＝90°.在△DOE和△BOF中，
∴△DOE≌△BOF(AAS)，
活动5 课堂小结
1．平行四边形对角线的性质．2．平行四边形对角线性质的运用．
四、作业布置与教学反思
1．作业布置 (1) 教材P49～51习题18.1第3，14，15题；2．教学反思