初中1 圆优质ppt课件

这是一份初中1 圆优质ppt课件，共22页。PPT课件主要包含了CONTENTS，学习目标，新课导入，新课讲解，课堂小结，当堂小练，拓展与延伸，布置作业等内容，欢迎下载使用。

1.圆的切线的判定；2.三角形的内切圆. （重点、难点）
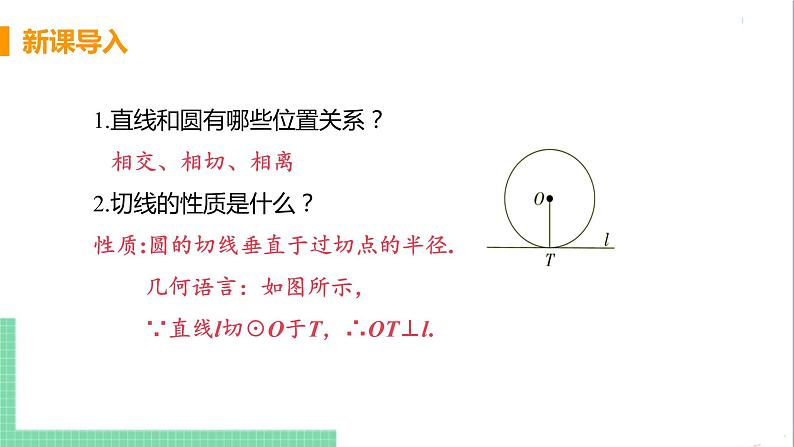
1.直线和圆有哪些位置关系？ 相交、相切、相离2.切线的性质是什么？性质:圆的切线垂直于过切点的半径. 几何语言：如图所示， ∵直线l切☉O于T，∴OT⊥l.
知识点1 圆的切线的判定
　　如图，在⊙O中，经过半径 OA 的外端点 A 作直线 l⊥OA，则圆心 O 到直线 l 的距离是多少？直线 l 和⊙O 有什么位置关系？
经过半径的外端并且垂直于这条半径的直线是圆的切线．
如图，已知AB 是⊙ O 的直径，AB=4， 点C 在线段AB 的延长线上， 点D 在⊙ O 上， 连接CD， 且CD=OA，OC=2 ，求证：CD 是⊙ O 的切线.
分析：利用“有切点，连半径，证垂直”判定圆的切线.
证明：连接OD.由题意可知CD=OD=OA= AB=2.∵ OC=2 ，∴ OD2+CD2=OC2.∴∠ ODC=90°，即OD ⊥ CD.又点D 在⊙ O 上，∴ CD 是⊙ O 的切线.
切线的判定方法有三种：①直线与圆有唯一公共点；②直线到圆心的距离等于该圆的半径；③切线的判定定理．即 经过半径的外端并且垂直这条半径的直线是圆的 切线.
1.下列四个命题：①与圆有公共点的直线是圆的切线；②垂直于圆的半径的直线是圆的切线；③到圆心的距离等于半径的直线是圆的切线；④过直径端点，且垂直于此直径的直线是圆的切线．其中是真命题的是(　　)A．①② B．②③ C．③④ D．①④
2.如图，△ABC是⊙O的内接三角形，下列选项中，能使过点A的直线EF与⊙O相切于点A的条件是(　　)A．∠EAB＝∠C B．∠EAB＝∠BACC．EF⊥AC D．AC是⊙O的直径
知识点2 三角形的内切圆
已知：△ABC(如图).求作： ⊙ I，使它与△ ABC的三边都相切.
作法：1.作∠B ， ∠C的平分线BE和CF,交点为I，如图.2.过I作BC的垂线，垂足为D.3.以I为圆心，以ID为半径作⊙I. ⊙I就是所求的圆.
定义：和三角形三边都相切的圆叫做三角形的内切 圆．内切圆的圆心是三角形三条角平分线的交点， 叫做三角形的内心．
下列关于三角形的内心和外心的说法中，正确的说法为（ ） ①三角形的内心是三角形内切圆的圆心； ②三角形的内心是三个角平分线的交点； ③三角形的外心到三边的距离相等； ④三角形的外心是三边中垂线的交点．A.①②③④ B.①②③C.①②④ D.②③④
1.如图，已知锐角三角形、直角三角形、钝角三角形，分别作出它们的内切圆.三 角形的内心是否都在三角形内部？
解：图略．三角形的内心都在三角形的内部．
2.下列说法错误的是(　　)A．三角形的内切圆与三角形的三边都相切B．一个三角形一定有唯一一个内切圆C．一个圆一定有唯一一个外切三角形D．等边三角形的内切圆与外接圆是同心圆
切线的三种判定方法：(1)定义；(2)数量关系；(3)位置关系(切线的判定定理)：经过半径外端并且 垂直于这条半径的直线是圆的切线． 在切线的三种判定方法中，常用的是后两种判定 方法，在判定圆的切线时，往往需要添加辅助线．
1.如图，AB是⊙O的直径，线段BC与⊙O的交点D是BC的中点，DE⊥AC于点E，连接AD，则下列结论中正确的个数是(　　) ①AD⊥BC；②∠EDA＝∠B；③OA＝ AC；④DE是⊙O的切线．A．1 B．2C．3 D．4
2.如图为4×4的网格图，A，B，C，D，O均在格点上，点O是(　　)A．△ACD的外心 B．△ABC的外心C．△ACD的内心 D．△ABC的内心
如图，点O为∠MPN的平分线上一点，以点O为圆心的⊙O与PN相切于点A. 求证：PM为⊙O的切线．