北师大版九年级下册第三章 圆7 切线长定理一等奖课件ppt

这是一份北师大版九年级下册第三章 圆7 切线长定理一等奖课件ppt，共20页。PPT课件主要包含了学习目标，新课导入，新课讲解，课堂小结，当堂小练，拓展与延伸，布置作业等内容，欢迎下载使用。

理解、掌握切线长定理的概念.（重点、难点）
前面我们已经学习了切线的判定和性质，已知⊙O和⊙O外一点P，你能够过点P画出⊙O的切线吗？1.猜想：图中的线段PA与PB有什么关系？2.图中还有哪些量？猜想它们之间有什么关系？
知识点1 切线长定理
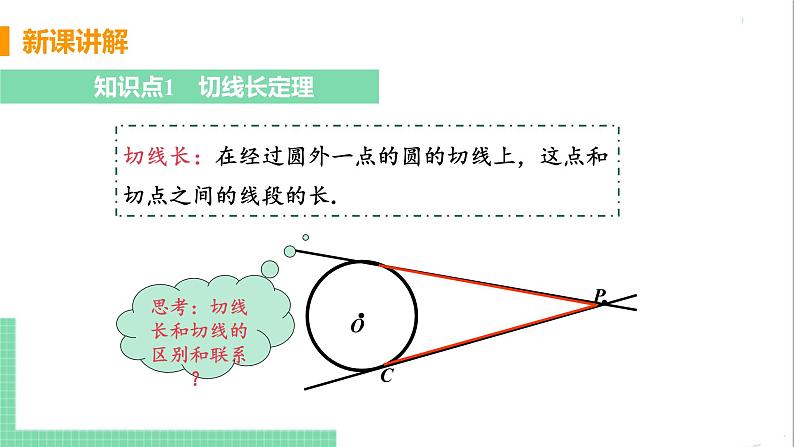
切线长：在经过圆外一点的圆的切线上，这点和切点之间的线段的长.
思考：切线长和切线的区别和联系？
切线是直线，不可以度量；切线长是指切线上的一条线段的长，可以度量.
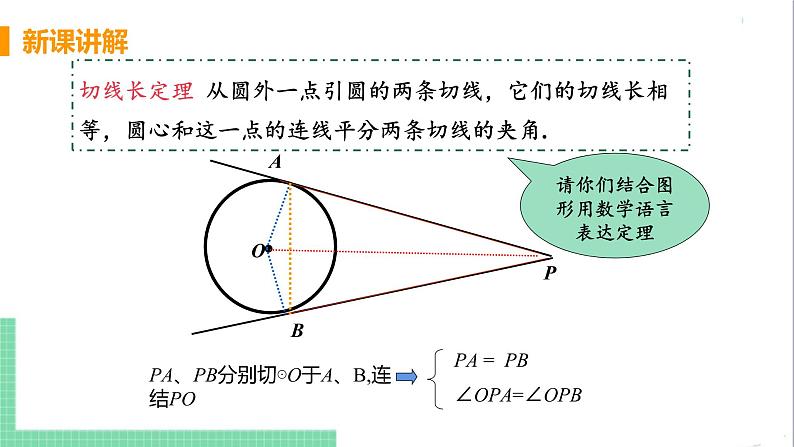
切线长定理 从圆外一点引圆的两条切线，它们的切线长相等，圆心和这一点的连线平分两条切线的夹角.
请你们结合图形用数学语言表达定理
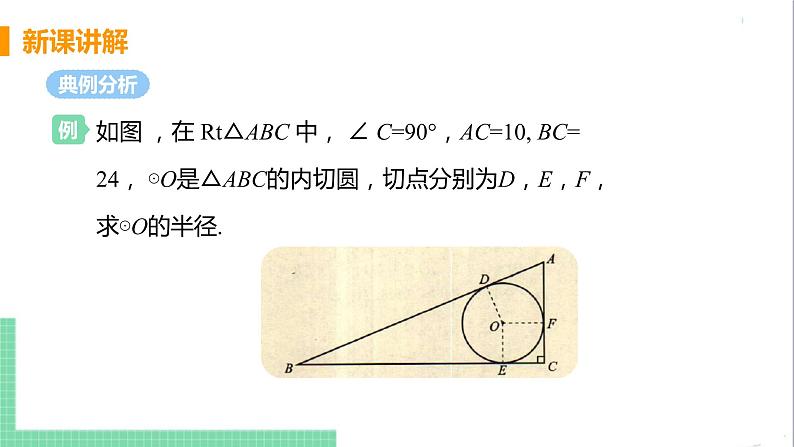
如图 ，在 Rt△ABC 中， ∠ C=90°，AC=10, BC=24， ⊙O是△ABC的内切圆，切点分别为D，E，F，求⊙O的半径.
连接OD，OE，OF，则OD=OE=OF,设OD=r. 在△ABC中，AC=10, BC=24，∴AB = = 26.∵ ⊙O分别与AB，BC, AC相切于点D，E，F，∴OD⊥AB，OE ⊥ BC, OF ⊥ AC，BD = BE， AD = AF，CE=CF.
又∵ ∠ C=90°,∴四边形OECF为正方形.∴ CE=CF=r.∴ BE = 24-r, AF=10-r.∴ AB = BD + AD = BE+AF =24-r+ 10-r= 34-2r.而AB = 26,∴ 34 -2r = 26.∴ r = 4,即⊙O 的半径为4.
1.已知⊙O的半径为3 cm，点P和圆心O的距离为6 cm. 过点P画⊙O的两条切线，求这两条切线的切线长.
如图，PA，PB为⊙O的切线．由题意可知OA＝3 cm，PO＝6 cm，OA⊥PA，∴PA＝ (cm)． 又由切线长定理知PA＝PB，∴PB＝33 cm.
2 下列说法正确的是(　　) A．过任意一点总可以作圆的两条切线 B．圆的切线长就是圆的切线的长度 C．过圆外一点所画的圆的两条切线长相等 D．过圆外一点所画的圆的切线长一定大于圆的半径
如图，PA，PB是⊙O的切线，切点分别为A，B，BC为⊙O的直径，连接AB，AC，OP.求证：(1)∠APB＝2∠ABC；(2)AC∥OP.
(1)由切线长定理知∠BPO＝∠APO＝ ∠APB， 而要证∠APB＝2∠ABC，即证明∠ABC＝ ∠APB＝∠BPO，利用同角的余角相等可证；(2)证明AC∥OP，可用AC⊥AB，OP⊥AB，也 可用同位角相等来证．
(1)∵PA，PB分别切⊙O于点A，B， ∴由切线长定理知∠BPO＝∠APO＝ ∠APB， PA＝PB， ∴PO⊥AB，∴∠ABP＋∠BPO＝90°. 又∵PB是⊙O的切线，∴OB⊥PB. ∴∠ABP＋∠ABC＝90°. ∴∠ABC＝∠BPO＝ ∠APB， 即∠APB＝2∠ABC.
(2)∵BC是⊙O的直径， ∴∠BAC＝90°，即AC⊥AB. 由(1)知OP⊥AB，∴AC∥OP.
为了测量一个圆形铁环的半径，某同学采用如下方法：将铁环平放在水平桌面上，用一个含有30°角的三角尺和一把刻度尺，按如图所示的方法得到相关数据，进而可求得铁环的半径．若P为切点，测得PA＝5 cm，则铁环的半径是________．
切线长定理 从圆外一点引圆的两条切线，它们的切线长相等，圆心和这一点的连线平分两条切线的夹角.
1.如图，PA，PB是⊙O的切线，且∠APB＝50°，下列结论不正确的是(　　)A．PA＝PB B．∠APO＝25°C．∠OBP＝65° D．∠AOP＝65°
2.如图，AB为半圆O的直径，AD，BC分别切⊙O于A，B两点，CD切⊙O于点E，AD与CD相交于点D，BC与CD相交于点C，连接OD，OC，对于下列结论：①OD2＝DE·CD；②AD＋BC＝CD；③OD＝OC；④S梯形ABCD＝ CD·OA；⑤∠DOC＝90°.其中正确的结论是(　　)A．①②⑤ B．②③④ C．③④⑤ D．①④⑤