人教版第十三章 轴对称13.1 轴对称13.1.1 轴对称试讲课课件ppt

这是一份人教版第十三章 轴对称13.1 轴对称13.1.1 轴对称试讲课课件ppt，共19页。PPT课件主要包含了学习目标，新课导入，新课讲解，课堂小结，当堂小练，拓展与延伸，布置作业，线段垂直平分线等内容，欢迎下载使用。

1.理解并掌握线段垂直平分线的定义.（重点） 2.熟悉轴对称图形和轴对称图形的性质.（难点） 3.综合运用轴对称图形的性质、线段垂直平分线来解决实际问题.
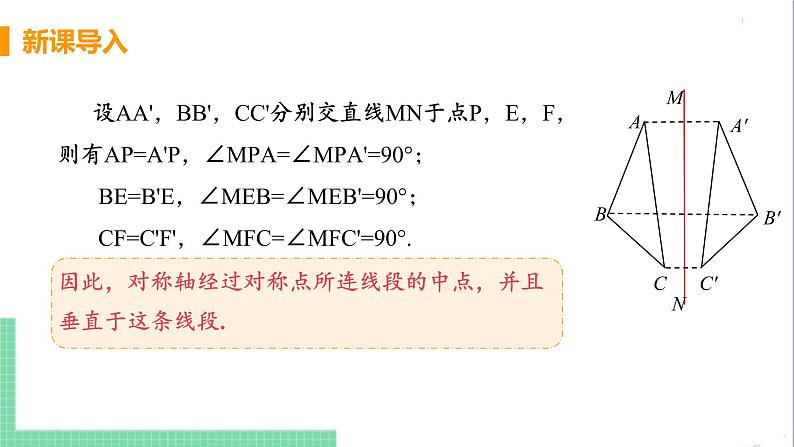
如图，△ABC和△A'B'C'关于直线MN对称，点A'，B'，C'分别是点A，B，C的对称点，线段AA'，BB'，CC'与直线MN有什么关系？
解：∵△ABC和△A'B'C'关于直线MN对称，∴将△ABC沿着MN折叠后能和△A'B'C'完全重合.∴点A和点A'，点B和点B'，点C和点C'是对称点.
设AA'，BB'，CC'分别交直线MN于点P，E，F，则有AP=A'P，∠MPA=∠MPA'=90°； BE=B'E，∠MEB=∠MEB'=90°； CF=C'F'，∠MFC=∠MFC'=90°.因此，对称轴经过对称点所连线段的中点，并且垂直于这条线段.
知识点1 线段的垂直平分线
几何语言：如图所示，直线l是线段AB的垂直平分线.则：AO=BO，l⊥AB.
1、线段的垂直平分线必须满足两个条件：①经过这条线段的中点；②垂直于这条线段.这二者缺一不可.2、线段的垂直平分线是一条直线.3、线段垂直平分线也可以称为“中垂线”.
知识点2 图形轴对称的性质
如图，五边形ABCDE是轴对称图形，直线MN是对称轴，则直线 MN是线段AD，BC的垂直平分线.
知识点2 图形轴对称的性质：
∵△ABC和△DEF关于直线MN 轴对称， ∴△ABC和△DEF全等. ∴∠B=∠E ，AB=DE ，AD的连线被直线MN垂直平分.
∵直线MN是四边形AMBN的对称轴，且点A和点B是对称点， ∴AM=BM，AN=BN，∠ANM=∠BNM. ∵点P是直线MN上的点，∴∠PAN=∠PBN，∠MAN=∠MBN.∴∠MAN-∠PAN=∠MBN-∠PBN，即∠MAP=∠MBP.
轴对称图形的对称轴，是任何一对对应点所连线段的垂直平分线
如果两个图形关于某条直线对称，那么对称轴是任何一对对应点所连线段的垂直平分线
经过线段中点并且垂直于这条线段的直线，叫做这条线段的垂直平分线
如图，在3×3的正方形网格中，有两个小正方形已被涂上阴影，再将图中剩余小正方形中任意一个涂上阴影，那么能使整个图案构成一个轴对称图形的涂法有（ ） A.5种 B.6种 C.4种 D.7种
分析：图中是3×3的正方形网格，已经涂上2个阴影，还剩下7个，选择合适的对称轴，根据轴对称图形的概念找出正确的图法，保证不重不漏.
如果三角形三条边的垂直平分线的交点在三角形的外部，那么这个三角形是（ ） A.直角三角形 B.锐角三角形 C.钝角三角形 D. 等边三角形
如图，在正方形中均匀分布着一些数字，小明利用轴对称的思想，用了一种非常简便的方法，迅速地将这些数字的和求了出来，你知道他是怎么求出来的吗？
正方形的数字之和10×10+5×5=125
（1）在△ABC中，AB=AC，AB的垂直平分线交AB于N，交BC的延长线于 M，∠A=50°，求∠NMB的大小.（2）如果将（1）中∠A的度数改为80°，其余条件不变，再求∠NMB的大小.（3）你发现有什么规律？请尝试证明.（4）将（1）中的∠A改为钝角，对这个问题发现的规律是否需要加以修改？
（1）解：∵AB的垂直平分线交AB于N， ∴∠MNB=∠MNA=90°. ∵∠B= （180°-∠A）=65°， ∴∠NMB=90°-∠B=25°.
（2）解：∵AB的垂直平分线交AB于N， ∴∠MNB=∠MNA=90°. ∵∠B= （180°-∠A）=50°， ∴∠NMB=90°-∠B=40°.
（3）证明：设∠A=a， ∵AB的垂直平分线交AB于N， ∴∠MNB=∠MNA=90°. ∵∠B= （180°-a） , ∴∠NMB=90°-∠B=a.