2021年中考数学考前小题抢分王：17梯形（含解析）

梯　形

一 、选择题(本大题共4小题，每小题4分，共16分)

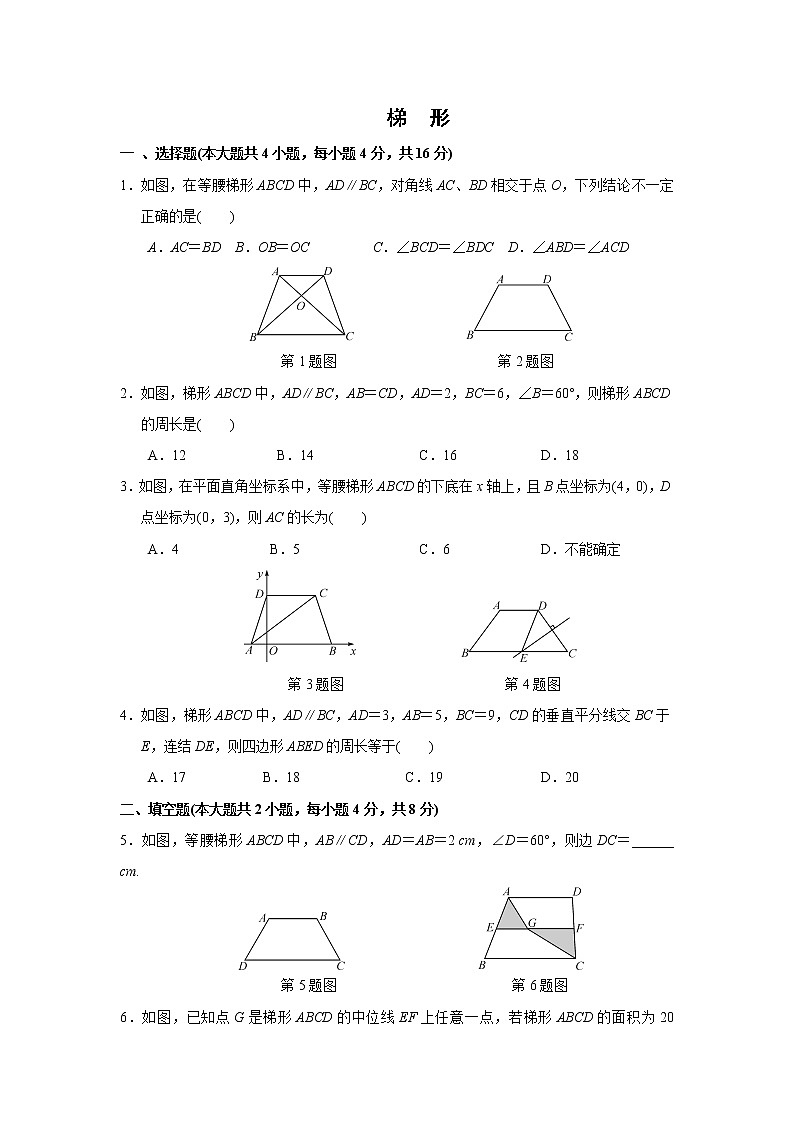
1．如图，在等腰梯形ABCD中，AD∥BC，对角线AC、BD相交于点O，下列结论不一定正确的是(　　)

A．AC＝BD  B．OB＝OC         C．∠BCD＝∠BDC  D．∠ABD＝∠ACD

第1题图                       第2题图

2．如图，梯形ABCD中，AD∥BC，AB＝CD，AD＝2，BC＝6，∠B＝60°，则梯形ABCD的周长是(　　)

A．12　　       　B．14　　         　C．16　　      　D．18

3．如图，在平面直角坐标系中，等腰梯形ABCD的下底在x轴上，且B点坐标为(4，0)，D点坐标为(0，3)，则AC的长为(　　)

A．4             B．5                 C．6             D．不能确定

第3题图                       第4题图

4．如图，梯形ABCD中，AD∥BC，AD＝3，AB＝5，BC＝9，CD的垂直平分线交BC于E，连结DE，则四边形ABED的周长等于(　　)

A．17           B．18               C．19              D．20

二、填空题(本大题共2小题，每小题4分，共8分)

5．如图，等腰梯形ABCD中，AB∥CD，AD＝AB＝2 cm，∠D＝60°，则边DC＝______ cm.

第5题图                         第6题图

6．如图，已知点G是梯形ABCD的中位线EF上任意一点，若梯形ABCD的面积为20 cm2，则图中阴影部分的面积为______．

三、解答题(本大题共4小题，共36分)

7．(6分)如图，等腰梯形ABCD中，AD∥BC，点E是AD延长线上的一点，且CE＝CD.

求证：∠B＝∠E.

8．(8分)如图所示，在梯形ABCD中，AD∥BC，∠BDC＝90°，E为BC上一点，∠BDE＝∠DBC.

(1)求证：DE＝EC；

(2)若AD＝BC，试判断四边形ABCD的形状，并说明理由．

9．(10分)我们知道“连接三角形两边中点的线段叫做三角形的中位线”，“三角形的中位线平行于三角形的第三边，且等于第三边的一半”，类似地，我们把连接梯形两腰中点的线段叫做梯形的中位线，如图，在梯形ABCD中，AD∥BC，点E，F分别是AB，CD的中点，那么EF就是梯形ABCD的中位线，通过观察、测量，猜想EF和AD，BC有怎样的位置和数量关系？并证明你的结论．

10．(12分)在梯形ABCD中，AD∥BC，AB＝CD，对角线AC、BD交于点O，AC⊥BD，E、F、G、H分别是AB、BC、CD、DA的中点．

(1)求证：四边形EFGH是正方形；

(2)若AD＝2，BC＝4，求四边形EFGH面积．

参考答案

1. C　解析：由等腰梯形的对称性，得选项A、B、D正确，而选项C不一定正确．

2. C　解析：过点D作DE∥AB，交BC于点E，又AD∥BC，所以四边形ABED为平行四边形，因为AB＝CD＝DE，∠C＝∠B＝60°，所以DC＝EC＝4，则梯形ABCD是周长是16.

3. B　解析：过点C作CE⊥x轴，垂足为E，∵B点坐标为(4，0)，D点坐标为(0，3)，∴OD＝3，OB＝4.

根据等腰梯形的性质，CE＝OD＝3，

BE＝OA，∴AE＝OB＝4.

在Rt△AEC中，AC＝

＝＝5.

4. A　解析：∵点E在CD的垂直平分线上，∴ED＝EC.

∵AD＝3，AB＝5，BC＝9，

∴四边形ABED的周长＝AB＋BE＋ED＋DA＝AB＋BE＋EC＋DA＝AB＋BC＋DA＝5＋9＋3＝17，故选A.

5. 4　解析：如图，过B点作BE∥AD交DC于E，因为AB∥DC，所以DE＝AB＝2，BE＝AD＝BC＝2，因为∠D＝∠C＝60°，所以EC＝BC＝BE＝2，所以DC＝DE＋EC＝2＋2＝4(cm)．

6. 5 cm2　解析：设梯形ABCD的高为2h，那么在△AEG和△CFG中，EF边上的高为h，S梯形ABCD＝2h·EF＝20，S△AEG＋S△CGF＝EG·h＋GF·h＝EF·h＝5，所以所求图中阴影部分的面积为5 cm2.

7. 证明：∵四边形ABCD是等腰梯形，AD∥BC，

∴∠B＝∠BCD，∠BCD＝∠EDC.

∵CE＝CD，∴∠EDC＝∠E，∴∠B＝∠E.(6分)

8. (1)证明：∵∠BDC＝90°，∴∠BDE＋∠EDC＝90°，

且∠DBC＋∠C＝90°.

又∵∠BDE＝∠DBC，∴∠EDC＝∠C，∴DE＝EC.(3分)

(2)四边形ABED为菱形．

理由：∵∠BDE＝∠DBC，∴BE＝DE.

∵DE＝EC，∴BE＝EC＝BC.∵AD＝BC，∴AD＝BE.

又∵AD∥BC，∴四边形ABED为平行四边形．(6分)

又∵BE＝DE，∴▱ABED为菱形．(8分)

9. 结论为：EF∥AD∥BC，EF＝(AD＋BC)．(2分)

证明：如图，连接AF并延长交BC的延长线于点G.

∵AD∥BG，∴∠DAF＝∠G.

在△ADF和△GCF中，

∴△ADF≌△GCF.∴AF＝FG，AD＝CG.(6分)

又∵AE＝EB，∴EF∥BG，EF＝BG.

即EF∥AD∥BC，EF＝(AD＋BC)．(10分)

10. (1)证明：在△ABC中，∵E、F分别是AB、BC的中点，

∴EF＝AC，EF∥AC.(2分)

同理FG＝BD，FG∥BD，GH＝AC， HE＝BD.

在梯形ABCD中，∵AB＝DC，∴AC＝BD.∴EF＝FG＝GH＝HE.

∴四边形EFGH是菱形．(4分)

∵EF∥AC，AC⊥BD，FG∥BD，∴EF⊥FG，

∴∠EFG＝90°，∴四边形EFGH是正方形．(6分)

(2)如图，连接EG.在梯形ABCD中，

∵E、G分别是AB、DC的中点，

∴EG＝(AD＋BC)＝3.(8分)

在Rt△EHG中，

∵EH2＋GH2＝EG2，EH＝GH，

∴EH2＝，

即四边形EFGH的面积为.(12分)