2020-2021学年第二章 相交线与平行线1 两条直线的位置关系精品课件ppt

这是一份2020-2021学年第二章 相交线与平行线1 两条直线的位置关系精品课件ppt，共31页。PPT课件主要包含了表示为直线m，角的表示，只有一个，不相交，对顶角相等等内容，欢迎下载使用。

表示为:直线AB ,(或)直线BA.
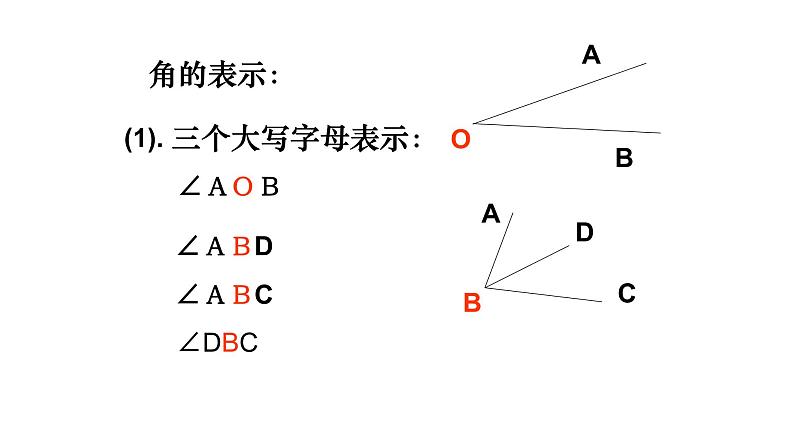
(1). 三个大写字母表示：　　∠ＡＯＢ
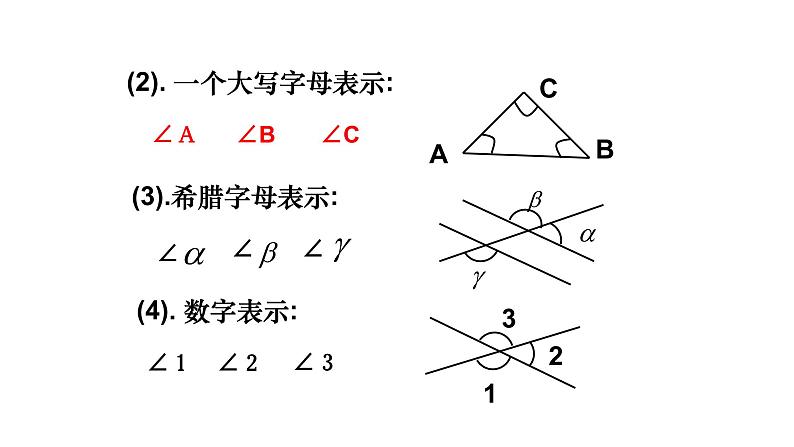
(2). 一个大写字母表示:
(3).希腊字母表示:
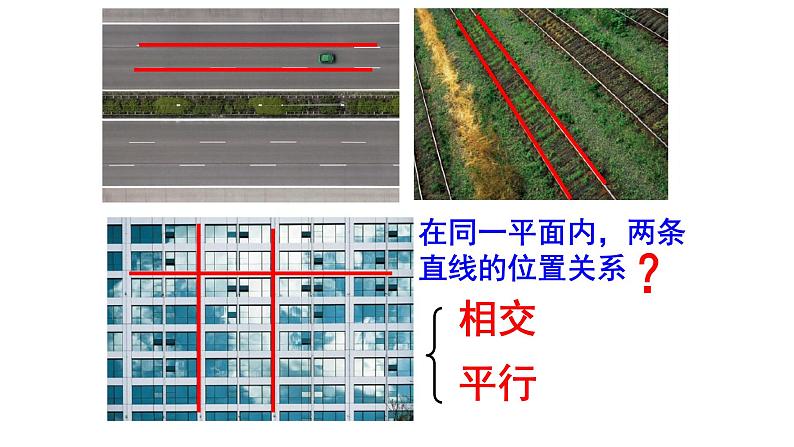
在同一平面内，两条直线的位置关系
在同一平面内，两条直线有两种位置关系： _____和_____.
在同一平面内，若两条直线_________公共点，我们称这两条直线为相交线.
在同一平面内，_______的两条直线叫做平行线.
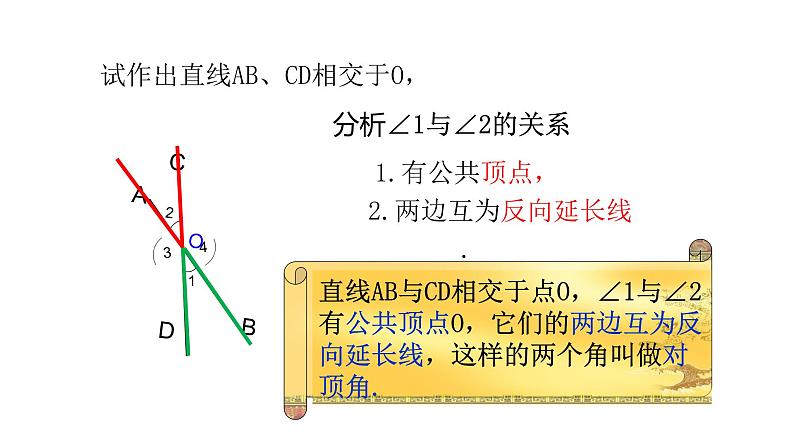
试作出直线AB、CD相交于O，
1.有公共顶点， 2.两边互为反向延长线.
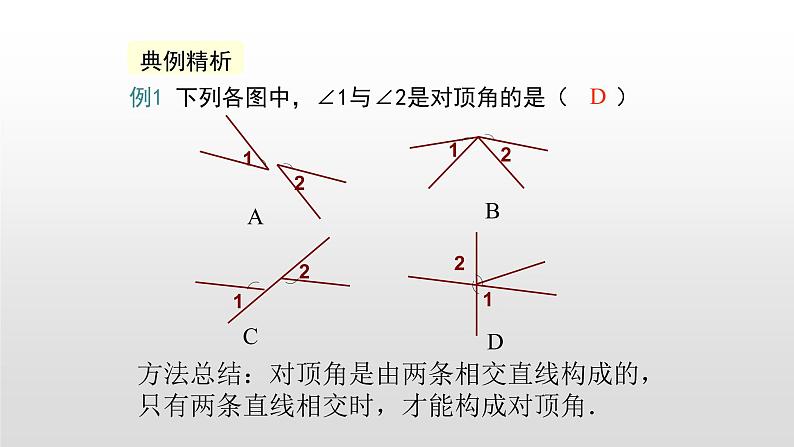
例1 下列各图中，∠1与∠2是对顶角的是（ ）
方法总结：对顶角是由两条相交直线构成的，只有两条直线相交时，才能构成对顶角．
请你观察图中∠1和∠2这组对顶角，你发现它们的大小有什么关系?
思考“相等的角是对顶角”这句话对吗？
如图直线AB与CD相交于点O，∠1和∠3有公共顶点O，并且它们的两边互为反向延长线，这样的两个角叫做对顶角.∠2和∠4也是对顶角.
如果两个角的和等于180°(平角)，就说这两个角互为补角(简称互补).可以说∠3是∠4的补角或∠4是∠3的补角.
如果两个角的和等于90°(直角)，就说这两个角互为余角(简称互余).可以说∠1是∠2的余角或∠2是∠1的余角.
练一练：图中所给的角，哪些互为余角？
练一练：图中给出的各角，哪些互为补角？
小组合作交流，解决下列问题：在图2中问题3：哪些角互为补角？哪些角互为余角？
因为∠1+∠2=90º，∠2+∠3=90º， 所以∠1= ∠3 ，理由是 同角的余角相等
因为∠1+∠2=180º，∠2+∠3=180º，所以∠1= ∠3 ，理由是同角的补角相等。
如图1，打台球时，选择适当的方向用白球击打红球，反弹后的红球会直接入袋，此时∠1=∠2，将图1简化成图2，ON与DC交于点O，∠DON=∠CON=900，∠1=∠2.
小组合作交流，解决下列问题：在图2中问题1：∠3与∠4有什么关系？为什么？
因为∠1= ∠2，∠ 1+∠3=90° , ∠ 2+∠4=90°，所以 ∠ 3=∠4.
归纳总结：同角(等角)的补角相等，同角(等角)的余角相等.
因为∠1= ∠2，∠1+∠AOC=180°, ∠ 2+∠BOD=180°，所以∠AOC=∠BOD.
小组合作交流，解决下列问题：在图2中问题2：∠AOC与∠BOD有什么关系？为什么？
7.如图,∠COD=∠EOD=90°, C、O、E在一条直线上, 且∠2= ∠4, 请说出∠1与∠3之间的关系?并试着说明理由?
∠1与∠3相等(等角的余角相等).