数学九年级上册2 用配方法求解一元二次方程优秀课件ppt

这是一份数学九年级上册2 用配方法求解一元二次方程优秀课件ppt，共20页。PPT课件主要包含了学习目标，新课导入，新课讲解，课堂小结，当堂小练等内容，欢迎下载使用。

1.二次三项式的配方2.用配方法解一元二次方程（重点、难点）
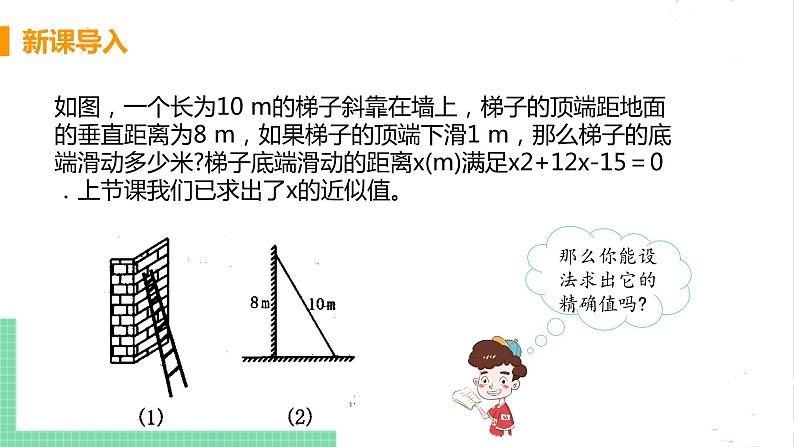
如图，一个长为10 m的梯子斜靠在墙上，梯子的顶端距地面的垂直距离为8 m，如果梯子的顶端下滑1 m，那么梯子的底端滑动多少米?梯子底端滑动的距离x(m)满足x2+12x-15＝0．上节课我们已求出了x的近似值。
那么你能设法求出它的精确值吗?
知识点1 二次三项式的配方
用利用完全平方式的特征配方，并完成填空． (1)x2＋10x＋________＝(x＋________)2； (2)x2＋(________)x＋ 36＝[x＋(________)]2; (3)x2－4x－5＝(x－________)2－______．
配方就是要配成完全平方，根据完全平方式的结构特征，当二次项系数为1时，常数项是一次项系数一半的平方．
1.将代数式a2＋4a－5变形，结果正确的是(　　)A．(a＋2)2－1 B．(a＋2)2－5C．(a＋2)2＋4 D．(a＋2)2－9
当二次项系数为1时，已知一次项的系数，则常数项为一次项系数一半的平方；已知常数项，则一次项系数为常数项的平方根的两倍．注意有两个．当二次项系数不为1时，则先化二次项系数为1，然后再配方．
一次项系数变为负又如何配方呢?
若x2＋2(m－3)x＋16是关于x的完全平方式， 则m________.
将代数式a2＋4a－5变形，结果正确的是(　　)A．(a＋2)2－1 B．(a＋2)2－5C．(a＋2)2＋4 D．(a＋2)2－9
知识点2 用配方法解一元二次方程
怎样解方程x2＋6x＋4＝0? 我们已经会解方程(x＋3)2＝5.因为它的左边是含有x 的完全平方式，右边是非负数，所以可以直接降次解方程．那么，能否将方程x2＋6x＋4＝0转化为可以直接降次的形式再求解呢？
解下列方程． (1)x2－8x＋1＝0；　　 (2)2x2＋1＝3x； (3)3x2－6x＋4＝0. (1)方程的二次项系数为1，直接运用配方法．　 (2)先把方程化成2x2－3x＋1＝0.它的二次项系数　　　 为2，为了便于配方，需将二次项系数化为1，　　　 为此方程的两边都除以2.　　 (3)与(2)类似，方程的两边都除以3后再配方．
解：　(1)移项，得　　　　　x2－8x＝－1.　　　配方，得　　　　　x2－8x＋42＝－1＋42，　　　　　　　(x－4)2＝15.　　　由此可得　　　　　　　　　　　　
　　(2) 移项，得 2x2－3x＝－1. 二次项系数化为1，得 配方，得 由此可得　　　　　　　　　　
(3)移项，得3x2－6x＝－4　　二次项系数化为1，得 配方，得 因为实数的平方不会是负数，所以 x 取任 何实数时， (x－1)2 都是非负数，上式都不成立，即原方程无实数根．　　　　
x2－2x + 12 ＝ + 12.
(x－1)2＝ .
—般地，如果一个一元二次方程通过配方转化成 (x＋n)2＝p (Ⅱ) 的形式，那么就有：(1)当p>0时，方程(Ⅱ)有两个不等的实数根 (2)当p＝0时，方程(Ⅱ)有两个相等的实数根x1＝x2＝－n；(3)当p<0时，因为对任意实数x，都有(x＋n)2≥0， 所以方程(Ⅱ)无实数根．
1.用配方法解下列方程时,配方有错误的是( )A.x2+8x+9=0可化为(x+4)2=25B.x2-2x-99=0可化为(x-1)2=100C.2t2-7t-4=0可化为t-742=8116D.3x2-4x-2=0可化为x-232=1092.把方程2x2-3x-2=0配方成(x+m)2=n的形式,则m,n的值分别是( )A.m=-34,n=2516B.m=-32,n=2516C.m=-34,n=2716D.m=-34,n=254
3.阅读材料:把形如ax2+bx+c的二次三项式(或其中一部分)配成完全平方式的方法叫配方法.配方法的基本形式是完全平方式的逆a2±2ab+b2=(a±b)2.请解决下列问题:(1)填空:a2-4a+4=(a-2)2. (2)若a2+2a+b2-6b+10=0,求a+b的值.(3)若a,b,c分别是△ABC的三边长,且a2+4b2+c2-2ab-6b-2c+4=0,试判断△ABC的形状,并说明理由.解:(2)∵a2+2a+b2-6b+10=0, ∴(a+1)2+(b-3)2=0,∴a=-1,b=3, ∴a+b=2.(3)△ABC为等边三角形.理由如下:∵a2+4b2+c2-2ab-6b-2c+4=0, ∴(a-b)2+(c-1)2+3(b-1)2=0,∴a-b=0,c-1=0,b-1=0,∴a=b=c=1, ∴△ABC为等边三角形.