北师大版九年级上册第四章 图形的相似2 平行线分线段成比例精品课件ppt

这是一份北师大版九年级上册第四章 图形的相似2 平行线分线段成比例精品课件ppt，共26页。PPT课件主要包含了学习目标，新课导入，新课讲解，课堂小结，当堂小练，拓展与延伸，布置作业，平行线分线断成比例等内容，欢迎下载使用。

1.理解并掌握平行线分线段成比例的基本事实及其推论，并能够进行简单的计算和推理。 （重点）2.能熟练运用平行线分线段成比例的基本事实及其推论计算线段的长度（重点）
你能不通过测量快速将一根绳子分成两部分，使得这两部分的比是2:3？
知识点1 平行线分线段成比例的基本事实
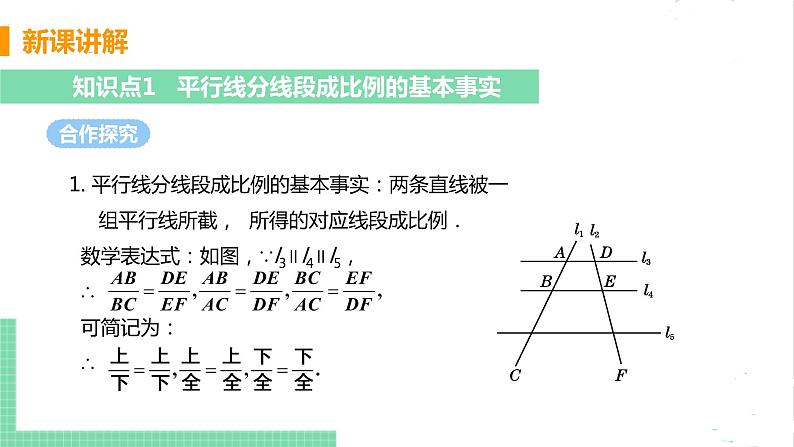
1. 平行线分线段成比例的基本事实：两条直线被一 组平行线所截， 所得的对应线段成比例． 数学表达式：如图，∵l3∥l4∥l5， ∴ 可简记为： ∴
(1)一组平行线两两平行，被截直线不一定平行； (2)所有的成比例线段是指被截直线上的线段，与 这组平行线上的线段无关； (3)当上比下的值为1时，说明这组平行线间的距离 相等．
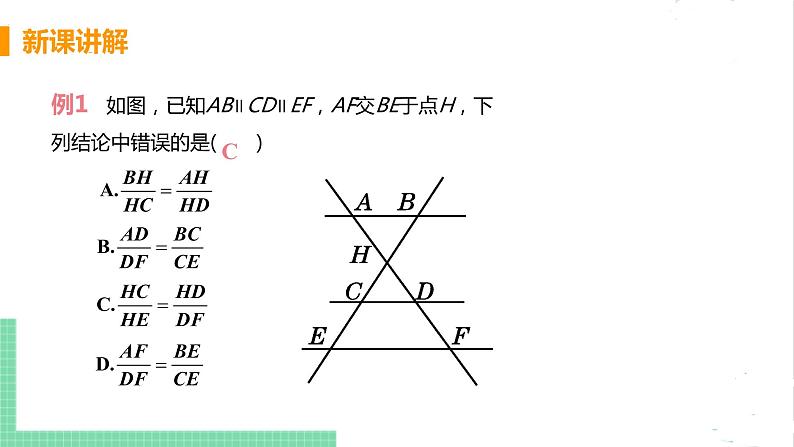
例1 如图，已知AB∥CD∥EF，AF交BE于点H，下列结论中错误的是(　　)
平行线分线段成比例的基本事实除基本图形外，主要还有“A”型和“X”型两种类型的图形，图包含这三种图形，从每种图形中找出比例线段即可判断出错误的选 项．∵AB∥CD∥EF，∴ 故选项A，B，D正确；∵CD∥EF，∴ 故选项C错误．
如图，AD∥BE∥CF，直线l1，l2与这三条平行线分别交于点A，B，C和点D，E，F，已知AB＝1，BC＝3，DE＝2，则EF的长为(　　)A．4 B．5 C．6 D．8
知识点2 平行线分线段成比例的基本事实推论
技巧1　中间比代换法证比例式
1． 如图，已知在△ABC中，点D，E，分别是边AB，AC，BC上的点，DE∥BC，EF∥AB.(1)求证： ；
(2)若AD∶DB＝3∶5，求CF∶CB.
解：∵AD∶DB＝3∶5，∴BD∶AB＝5∶8.∵DE∥BC，∴CE∶AC＝BD∶AB＝5∶8.∵EF∥AB，∴CF∶CB＝CE∶AC＝5∶8.
技巧2　等积代换法证比例式
2．如图，在△ABC中，D是AB上的一点，E是△ABC内一点，DE∥BC，过点D作AC 的平行线交CE的延长线于F，CF与AB交于P.求证：
证明：∵DE∥BC，∴ ∴PD·PC＝PE·PB.∵DF∥AC，∴ ∴PD·PC＝PF·PA.∴PE·PB＝PF·PA. ∴
技巧3　等比代换法证比例式
3．如图，E为▱ABCD的边CD延长线上的一点，连接BE，交AC于O，交AD于F.求证：BO2＝OF·OE.
技巧4　平行法证比例式
证明：∵△ABC与△DCE都是等边三角形，∴AC＝BC，CE＝CD，∠ACB＝∠DCE＝60°.∴∠ACB＋∠ACD＝∠DCE＋∠ACD，即∠ACE＝∠BCD.∴△ACE≌△BCD(SAS)．
技巧5　等比例过渡法证线段相等
1.如图,已知AB∥CD∥EF,BD∶DF=1∶2,那么下列结论正确的是( )A.AC∶AE=1∶3 B.CE∶EA=1∶3C.CD∶EF=1∶2 D.AB∶CD=1∶2 2.如图,已知AB∥CD∥EF,它们依次交直线l1于点A,D,F,交直线l2于点B,C,E,如果AD∶DF=3∶1,BE=10,那么CE等于( )A.103 B.203 C.52 D.152
3.如图,AD是△ABC的中线,E是AD上一点,且AE∶ED=2∶3,CE的延长线交AB于点F,若AF=3 cm,求AB的长.
解: 如答图,过点D作DH∥CF交AB于点H,则FHHB=CDBD=1,AFFH=AEED=23,∴FH=HB,3FH=23,解得FH=4.5.∴AH=AF+FH=7.5,HB=FH=4.5,∴AB=AH+HB=12. 故AB的长为12 cm.