数学九年级上册4 探索三角形相似的条件精品课件ppt

这是一份数学九年级上册4 探索三角形相似的条件精品课件ppt，共19页。PPT课件主要包含了学习目标，新课导入，新课讲解，课堂小结，当堂小练，拓展与延伸，布置作业，一定相似，相似三角形等内容，欢迎下载使用。

1.理解相似三角形的定义. 2.掌握用角的关系判定两三角形相似定理. （重点）
相似多边形的定义是什么？
观察两副三角尺如图，其中同样角度（30°与60°,或45°与45°)的两个三角尺大小可能不同，但它们看起来是相似的．一般地，如果两个三角形有两组对应角相等，它们一定相似吗？
知识点1 相似三角形的定义
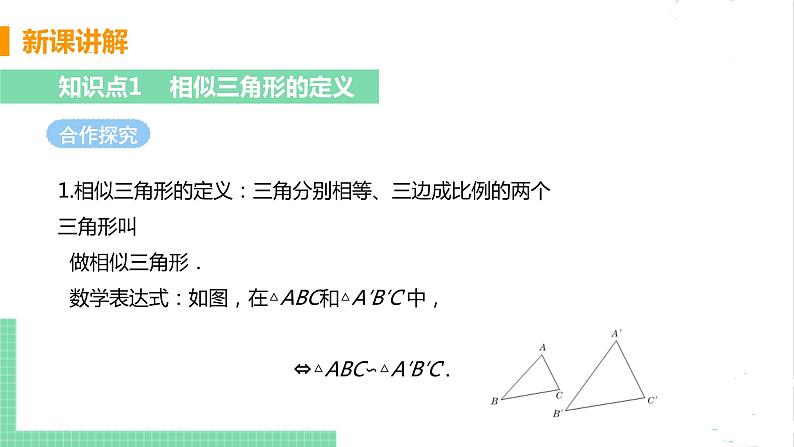
1.相似三角形的定义：三角分别相等、三边成比例的两个三角形叫 做相似三角形． 数学表达式：如图，在△ABC和△A′B′C′中， ⇔△ABC∽△A′B′C′.
(1)判定两个三角形相似的必备条件：三角分别相等， 三边成比例； (2)两个三角形相似又为解题提供了条件； (3)相似三角形具有传递性，即若 △ABC∽△A′B′C′， △A′B′C′∽△A″B″C″，则 △ABC∽△A″B″C″； (4)相似比为1的两个相似三角形全等，反过来两个 全等三角形可以看作是相似比是1的相似三角形．
3．易错警示：(1)表示两个三角形相似时，要注意对应性，即要把 对应顶点写在对应位置上．(2)求两个相似三角形的相似比，要注意顺序性．若 当△ABC∽△A′B′C′时， 则当△A′B′C′∽△ABC时，
1.下列说法中错误的是(　　)A．两个全等三角形一定相似B．两个直角三角形一定相似C．两个相似三角形的对应角相等，对应边成比例D．相似的两个三角形不一定全等2.如图，△ABC与△ADE相似，且∠ADE＝∠B，则下列比例式中正确的是(　　)
知识点2 用角的关系判定两个三角形的相似定理
如果两个三角形只有一个角相等，它们一定相似吗？如果有两个角分别相等呢？ 与同伴合作，两个人分别画△ABC和△A′B′C′,使得∠A和∠A′都等于∠α ，∠B和∠B′都等于∠β ，此时∠C与∠C′相等吗？三边的比 相等吗？这样的两个三角形相似吗？改变∠α ，∠β的大小，再试一试.
1.相似三角形的判定定理：两角分别相等的两个三角形相似． 数学表达式：在△ABC与△A′B′C′中，∵∠A＝∠A′，∠B ＝∠B′，∴△ABC∽△A′B′C′.2.常见的相似三角形类型： (1)平行线型：如图①，若DE∥BC，则△ADE∽△ABC. (2)相交线型：如图②，若∠AED＝∠B，则△AED∽△ABC. (3)“子母”型：如图③，若∠ACD＝∠B，则△ACD∽△ABC. (4)“K”型：如图④，若∠A＝∠D＝∠BCE＝90°，则△ACB∽△DEC，整体像一个横放的字母K，可以称为“K”型相似．
如图所示的三个三角形中，相似的是(　　)A．(1)和(2) B．(2)和(3)C．(1)和(3) D．(1)和(2)和(3)
如图，点P 是四边形ABCD边AB上一点，射线CP交DA的延长线于点E，则图中相似的三角形有(　　)A．0对 B．1对 C．2对 D．3对
两角分别相等的两个三角形相似．
1.下列条件一定能判定两个等腰三角形相似的是( )A.都含有一个40°的内角B.都含有一个50°的内角C.都含有一个60°的内角D.都含有一个70°的内角2.如图,在△ABC中,点D,E分别在边AB,AC上,DE∥BC,∠ACD=∠B,那么下列结论不正确的是( )A.△ADE∽△ABC B.△CDE∽△BCDC.△ADE∽△ACD D.△ADE∽△DBC
3.如图,在△ABC中,CF⊥AB于点F,ED⊥AB于点D,∠1=∠2,求证:△AFG∽△ABC.
证明:∵CF⊥AB,ED⊥AB,∴∠EDB=∠CFA=90°,∴∠1+∠B=∠2+∠AFG=90°.又∵∠1=∠2,∴∠AFG=∠B.又∵∠FAG=∠BAC,∴△AFG∽△ABC.