





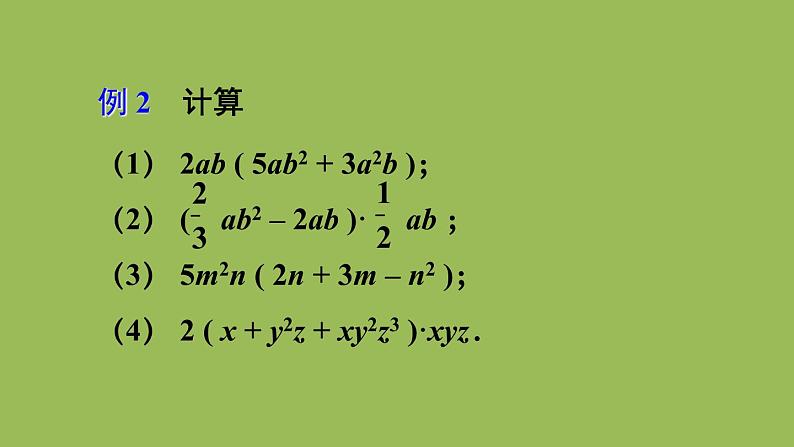
所属成套资源:北师大版七年级数学下册全册课件PPT
初中北师大版4 整式的乘法背景图课件ppt
展开
这是一份初中北师大版4 整式的乘法背景图课件ppt,共20页。PPT课件主要包含了4x5y3,2a5b5c5,由此可知,乘法分配律,例2计算,由题意得,b–2等内容,欢迎下载使用。
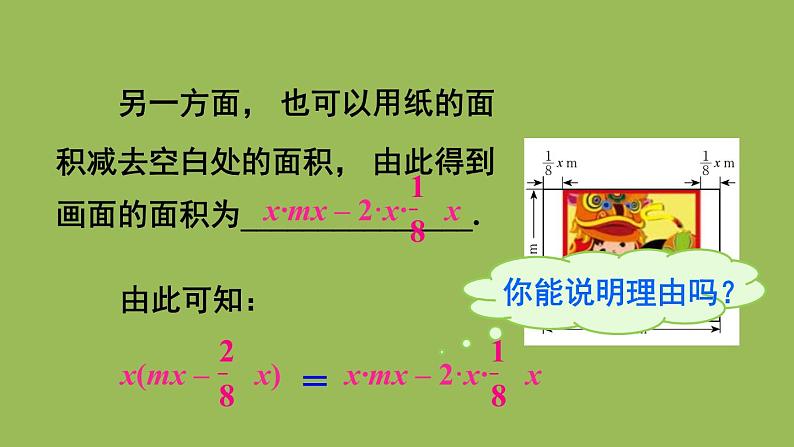
宁宁也作了一幅画, 所用纸的大小如图所示, 她在纸的左、右两边各留了 m 的空白,这幅画的画面面积是多少?
一方面, 可以先表示出画面的长与宽, 由此得到画面的面积为_______________;
另一方面, 也可以用纸的面积减去空白处的面积, 由此得到画面的面积为_______________.
(1) ab·(abc + 2x) 及 c2·(m + n – p) 等于什么? 你是怎样计算的?
ab·(abc + 2x) = ab·abc+ab·2x
= a2b2c+2abx
c2·(m + n – p) = c2m+c2n – c2p
(1) 2ab ( 5ab2 + 3a2b ); (2) ( ab2 – 2ab )· ab ;
(3) 5m2n ( 2n + 3m – n2 );(4) 2 ( x + y2z + xy2z3 )·xyz.
(– 2x)(x2 – x + 1); a(a2 + a) – a2(a – 2).
解(1)(– 2x)(x2 – x + 1)= (– 2x)x2 + (– 2x)·(– x) + (– 2x)·1= – 2x3 + 2x2 – 2x.
(2)a(a2 + a) – a2(a – 2)= a·a2 + a·a – a2·a + 2a2= a3 + a2 – a3 + 2a2= 3a2.
2a(a – b) – b(2a – b) + 2ab,其中 a = 2,b = – 3
解: 原式 = 2a2 – 2ab – 2ab + b2 + 2ab
= 2a2 – 2ab + b2
当 a = 2,b= – 3 时,
原式 = 2a2 – 2ab + b2
= 2×22 – 2×2×(– 3)+(– 3)2
= 8 + 12+ 9
若 – 2x2y(– xmy+3xy3)= 2x5y2 – 6x3yn,求m,n.
解: – 2x2y(– xmy+3xy3)= 2x5y2 – 6x3yn
2x2+my2 – 6x3y4 = 2x5y2 – 6x3yn
2 + m = 5,n = 4.
所以 m = 3,n = 4.
1.计算:(1) 5x · (3x + 4)
解:(1) 5x · (3x + 4)= 15x2 + 20x
(2) 原式 = – 15a3 + 4a2 – 3a
2. 某长方体的长为 a + 1,宽为 a,高为 3, 问这个长方体的体积是多少?
解: (a + 1) · a×3= 3a(a + 1)= 3a2 + 3a
3. 要使 x(x2 + a + 3) = x(x2 + 5) + 2(b + 2) 成立,则常数 a,b 的值分别为多少?
解:∵ x(x2 + a + 3) = x(x2 + 5) + 2(b + 2) ∴ x3 + (a + 3)x = x3 + 5x + 2(b + 2)
(a + 3) = 5
2(b + 2) = 0
4. 如果 y = Rx + b,当 x = R – 1 时,求 y 的值.
解:y = Rx + b = R(R – 1 )+ b = R2 – R + b
解:yn(yn + 9y – 12) – 3(3yn+1 – 4yn) = y2n + 9yn+1 – 12yn – 9yn+1 + 12yn = y2n 当 y = – 3,n = 2 时, 原式 =(– 3)2×2 =(– 3)4 = 81.
5. 先化简,再求值:yn(yn + 9y – 12) – 3(3yn+1 – 4yn), 其中 y = – 3,n = 2.
相关课件
这是一份初中数学北师大版七年级下册4 整式的乘法评课课件ppt,共18页。PPT课件主要包含了教学目标,新课导入,复习引入,4x5y3,新知探究,单项式与多项式相乘,pa+b+c,a+b+c,pa+pb+pc,根据乘法的分配律等内容,欢迎下载使用。
这是一份北师大版七年级下册4 整式的乘法完美版ppt课件,文件包含142单项式与多项式相乘pptx、142单项式乘多项式教学设计docx等2份课件配套教学资源,其中PPT共19页, 欢迎下载使用。
这是一份北师大版七年级下册4 整式的乘法课前预习课件ppt,共19页。PPT课件主要包含了教学目标,新课导入,复习引入,4x5y3,新知探究,单项式与多项式相乘,pa+b+c,a+b+c,pa+pb+pc,根据乘法的分配律等内容,欢迎下载使用。










