数学4.1 平面上两条直线的位置关系综合与测试公开课教学设计

4.1.1  相交与平行

教学目标

1.经历观察教具模式的演示和通过画图等操作,交流归纳与活动,进一步发展空间观念.毛

2.了解平行线的概念、平面内两条直线的相交和平行的两种位置关系, 知道平行公理以及平行公理的推论.

3.会用符号语言表示平行公理推论, 会用三角尺和直尺过已知直线外一点画这条直线的平行线.

教学重点

探索和掌握平行公理及其推论.

教学难点

对平行线本质属性的理解,用几何语言描述图形的性质.   

教学过程

一、问题情境

1．经过一点可以画几条直线？经过两点呢？经过三点呢？

2．①两条直线相交有        个交点.

②平面内两条直线的位置关系除相交外，还有哪些呢？

3．线段AB＝CD，CD＝EF，那么AB与EF的关系怎样？

二、新课学习

（一）平行线

1．观察思考：展示学具，在转动a的过程中，有没有直线a与直线b不相交的位置呢？

2．定义及表示方法：在同一平面内，                     是平行线.

直线a与b平行，记作          .

3．对平行线概念的理解：定义中强调“在同一平面内”，为什么要强调这句话.

在同一平面内,两条直线有几种位置关系? 在空间中，是否存在既不平行又不相交的两条直线? （提示：用长方体来说明 ）                                                  

4．总结：同一平面内两条直线的位置关系有两种：（1）        （2）         .

请你举出一些生活中平行线的例子.

（二）画平行线

1.     工具：直尺、三角板
2.     方法：一“落”；二“靠”；三“移”；四“画”.

3．请你根据此方法练习画平行线：

已知:直线a,点B,点C.

(1)过点B画直线a的平行线,能画几条?

(2)过点C画直线a的平行线,它与过点B的平行线平行吗?

（三）平行公理及推论

1．思考：上图中，①过点B画直线a的平行线，能画       条；

                 ②过点C画直线a的平行线，能画       条；

                 ③你画的直线有什么位置关系？                .

2．平行公理

①公理内容：                                        .

②比较平行公理和垂线的第一条性质：

共同点:都是“                 ”,这表明与已知直线平行或垂直的直线存在并且是唯一的.

不同点:平行公理中所过的“一点”要在已知直线外,两垂线性质中对“一点”没有限制,可在直线上,也可在直线外.

3．推论：                                                            .

①符号语言：∵b∥a，c∥a（已知）

∴b∥c（如果两条直线都与第三条直线平行,

那么这两条直线也互相平行）

②探索：如图,P是直线AB外一点,CD与EF相交于P.若CD与AB平行,则EF与AB平行吗?为什么?

三、实效训练

1．下列命题：（1）长方形的对边所在的直线平行；（2）经过一点可作一条直线与已知直线平行；（3）在同一平面内，如果两条直线不平行，那么这两条直线相交；（4）经过一点可作一条直线与已知直线垂直．其中正确的个数是（    ）

A．1          B．2          C．3          D．4

2.下列推理正确的是 （     ）

A．因为a//d, b//c,所以c//d    B.因为a//c, b//d,所以c//d

C.因为a//b, a//c,所以b//c     D.因为a//b, d//c,所以a//c

3.在同一平面内有三条直线,若其中有两条且只有两条直线平行,则它们交点的­个数为(   )

A.0个     B.1个     C.2个    D.3个

4.在同一平面内,两条直线的位置关系有_______    __.

5.在同一平面内,一条直线和两条平行线中的一条直线相交,那么这条直线与平行线中的另一条必__________.

6.同一平面内,两条相交直线不可能与第三条直线都平行,这是因为_____              ___.

7.两条直线相交,交点的个数是________,两条直线平行,交点的个数是_____个.

8.在同一平面内，与已知直线L平行的直线有          条，而经过L外一点，与已知直线L平行的直线有且只有    条.

四、小结与反思

1．本节课你有哪些收获？你还有哪些疑惑？

2．预习时的疑难解决了吗？

五、课后作业

课本P74.1,P75.2，3

4.1.2  相交直线所成的角(1)

教学目标

1.通过动手观察、操作、推断、交流等数学活动,进一步发展空间观念,培养识图能力、推理能力和有条理表达能力.毛

2.在具体情境中了解邻补角、对顶角, 能找出图形中的一个角的邻补角和对顶角,理解对顶角相等,并能运用它解决一些问题.

教学重难点

对顶角相等的性质及应用.  

教学过程

一、问题情境

1．在同一平面内的两条直线有几种位置关系？

2．经过直线外一点怎样画出这条直线的平行线？

3．如果两条直线都与第三条直线平行，那么这两条直线　　　　

即：如果b∥a，c∥a，那么b　　 c.

二、新课学习

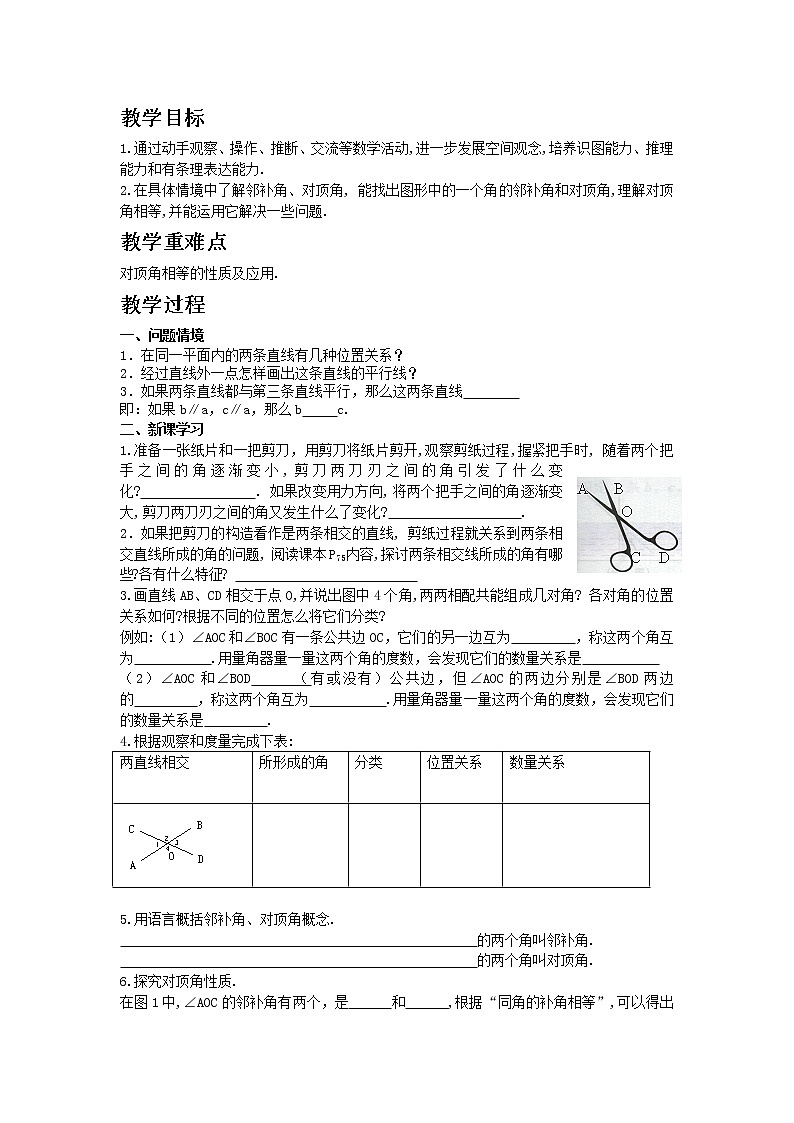
1.准备一张纸片和一把剪刀，用剪刀将纸片剪开,观察剪纸过程,握紧把手时, 随着两个把手之间的角逐渐变小,剪刀两刀刃之间的角引发了什么变化?                . 如果改变用力方向,将两个把手之间的角逐渐变大,剪刀两刀刃之间的角又发生什么了变化?                   .

2．如果把剪刀的构造看作是两条相交的直线, 剪纸过程就关系到两条相交直线所成的角的问题, 阅读课本P75内容,探讨两条相交线所成的角有哪些?各有什么特征?                          

3.画直线AB、CD相交于点O,并说出图中4个角,两两相配共能组成几对角? 各对角的位置关系如何?根据不同的位置怎么将它们分类?

例如:（1）∠AOC和∠BOC有一条公共边OC，它们的另一边互为         ，称这两个角互为           .用量角器量一量这两个角的度数，会发现它们的数量关系是          

（2）∠AOC和∠BOD     （有或没有）公共边，但∠AOC的两边分别是∠BOD两边的         ，称这两个角互为           .用量角器量一量这两个角的度数，会发现它们的数量关系是         .

4.根据观察和度量完成下表:

5.用语言概括邻补角、对顶角概念.

                                                   的两个角叫邻补角.

                                                   的两个角叫对顶角.

6.探究对顶角性质.

在图1中,∠AOC的邻补角有两个，是      和      ,根据“同角的补角相等”,可以得出     =      ,而这两个角又是对顶角，由此得到对顶角性质:对顶角相等.

注意：对顶角概念与对顶角性质不能混淆，对顶角的概念是确定两角的位置关系,对顶角性质是确定为对顶角的两角的数量关系.

你能利用“对顶角相等”这条性质解释剪刀剪纸过程中所看到的现象吗？

7.例题示范:如图,直线a,b相交,∠1=40°,求∠2,∠3,∠4的度数.

提示：未知角与已知角有什么关系？通过什么途径去求

这些未知角的度数？,规范地写出求解过程.

三、实效训练

1.如图所示,∠1和∠2是对顶角的图形有(   )毛

 A.1个         B.2个        C.3个          D.4个

2.如右图,三条直线AB,CD,EF相交于一点O, ∠AOD的对顶角是_____,

∠AOC的邻补角是_______，若∠AOC=50°,则∠BOD=______,

∠COB=_______，∠AOE+∠DOB+∠COF=_____.

3.如图，直线AB,CD相交于O,OE平分∠AOC,若∠AOD-∠DOB=50°,求∠EOB的度数.

四、小结与反思

本节课你有哪些收获？你还有哪些疑惑？

五、课后作业

课本P78  4，5.

4.1.2  相交直线所成的角(2)

教学目标

1．理解三线八角的意义，并能从复杂图形中识别它们

2．通过三线八角的特点的分析，培养学生抽象概括问题的能力

3．使学生认识图形是由简到繁组合而成，培养学生形成基本图形的结构的能力

教学重难点

三线八角的意义是重点，能在各种变式的图形中找出这三类角既是重点，也是难点

教学过程

一、问题情境

1．两条直线相交后产生了几个角?每两个角之间的关系是什么?

2．三条直线之间也可以有什么样的位置关系?

上节课是对相交的两条直线所形成的四个角进行研究，今天我们就对三条直线相交后形成的八个角进行研究，简称为：三线八角。

二、新课学习

1.讲解同位角、内错角、同旁内角的概念　　　　　　　　

同位角：我们把具有∠1和∠5这种位置关系的一对角叫作同位角.（∠1和∠5分别在直线AB和CD的同一方向，并且都在直线EF的同侧）

内错角：我们把具有∠3和∠5这种位置关系的一对角叫作内错角.(∠3和∠5都在直线AB,CD之间，并且分别在直线EF两侧)

同旁内角：我们把具有∠3和∠6这种位置关系的一对角叫作同旁内角.（∠3和∠6都在直线AB,CD之间，但它们在直线EF的同一旁）

思考：你还能从图中找出其他的同位角、内错角和同旁内角吗？

2．例题示范

例1 ： 如图，直线EF与AB,CD相交，构成8个角，指出图中所有的对顶角、同位角、内错角和同旁内角.

学生自己找，教师巡视指导

例2 ：如图，直线AB,CD被直线MN所截，同位角∠1与∠2相等，那么内错角∠2与∠3相等吗？

解  因为∠1=∠3 （对顶角相等）

    ∠1=∠2   （已知）

   所以∠2=∠3  （等量代换）

小结：两条直线被第三条直线所截，如果有一对同位角相等，则内错角相等.

3．应用“对顶角相等”及“等量代换”及等式的性质，还可以得出相应的一些结论：

（1）两条直线被第三条直线所截，如果有一对同位角相等，那么其他几对同位角也相等，并且内错角也相等，同旁内角互补.

（2）两条直线被第三条直线所截，如果有一对内错角相等，那么其他几对内错角也相等，并且同位角也相等，同旁内角互补.

（3）两条直线被第三条直线所截，如果有一对同旁内角互补，那么另一对同旁内角也互补，并且同位角相等，内错角也相等.

三、实效训练

1．练习P77练习第3题　

2．如图：下列各对角是什么角，它们是由

哪两条直线被哪条直线所截形成的？

①∠2和∠3  ②∠1和∠4  ③∠1和∠3

2、如图，填写理由

已知：∠1=∠2

    ∵∠2=∠4（             ）

    ∴∠1=∠4（             ）

又∵∠3+∠4=180°（          ）

  ∴∠1+∠3=180°（          ）

四、小结与反思

本节课你有哪些收获？你还有哪些疑惑？

五、作业

课本P78  6，7.