初中数学人教版九年级上册24.3 正多边形和圆一等奖课件ppt

这是一份初中数学人教版九年级上册24.3 正多边形和圆一等奖课件ppt，共30页。PPT课件主要包含了知识回顾，圆内接四边形的性质，学习目标，课堂导入，知识点1，新知探究，什么叫做正多边形，正多边形的对称性，圆内接正多边形，圆的外切正n边形等内容，欢迎下载使用。

1.对角互补；2.四个内角的和是360°；3.任一外角与其相邻的内角的对角相等(即外角等于内对角)．
1.了解正多边形和圆的有关概念.
2.理解并掌握正多边形半径、中心角、边心距、边长之间的关系.
3.会应用正多边形和圆的有关知识解决实际问题.
下面这些美丽的图案，都是在日常生活中我们经常能看到的.你能从这些图案中找出类似的图形吗?
各边相等、各角也相等的多边形叫做正多边形.
矩形是正多边形吗？为什么？菱形是正多边形吗？为什么？
不是，因为矩形不符合各边相等；
不是，因为菱形不符合各角相等；
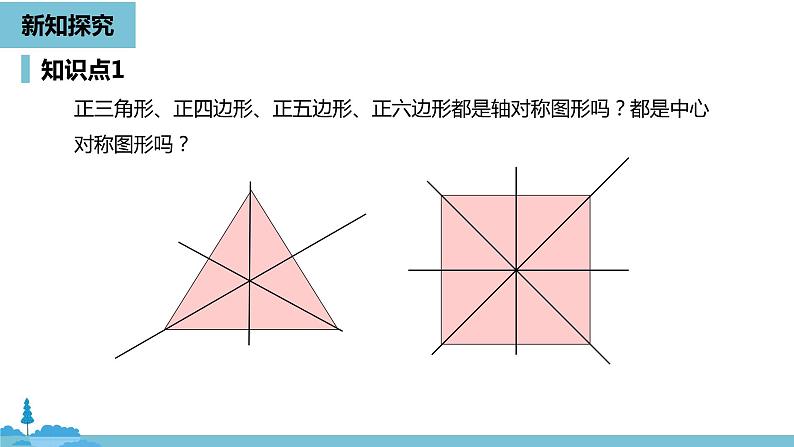
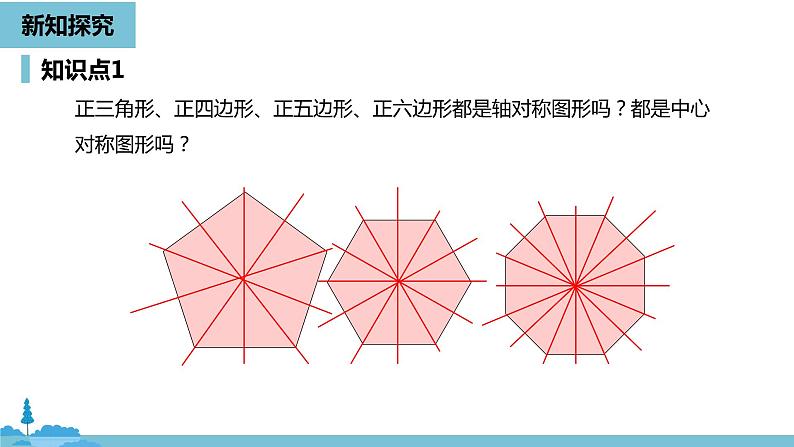
正三角形、正四边形、正五边形、正六边形都是轴对称图形吗？都是中心对称图形吗？
所有的正多边形都是轴对称图形，一个正n边形共有n条对称轴，每条对称轴都通过正n边形的中心.n为偶数时，它还是中心对称图形，它的中心就是对称中心.
以正四边形为例，根据对称轴的性质，你能得出什么结论？
EF是边AB，CD的垂直平分线，∴OA=OB，OD=OC.GH是边AD，BC的垂直平分线，∴OA=OD，OB=OC.∴OA=OB=OC=OD.
∴正方形ABCD有一个以点O为圆心的外接圆.
AC平分∠DAB及∠DCB，BD平分∠ABC及∠ADC，
∴OE=OH=OF=OG.
∴正方形ABCD还有一个以点O为圆心的内切圆.
所有的正多边形是不是都有一个外接圆和一个内切圆？
任何正多边形都有一个外接圆和一个内切圆.
任意三角形都有外接圆和内切圆，但是只有正三角形的外接圆和内切圆是同心圆；任意多边形不一定有外接圆和内切圆，但当多边形是正多边形时，一定有一个外接圆和一个内切圆，并且这两个圆是同心圆.
正多边形的外接圆和内切圆的公共圆心，叫做正多边形的中心.
外接圆的半径叫做正多边形的半径.
中心到正多边形的一边的距离叫做正多边形的边心距.
把圆分成n(n≥3)等份，依次连接各分点得到的多边形就是这个圆的内接正n边形，这个圆就是这个正n边形的外接圆.
把圆分成n(n≥3)等份，经过各分点作圆的切线，以相邻切线的交点为顶点的多边形是这个圆的外切正n边形.一定要注意正多边形的半径是指外接圆的半径，而不是内切圆的半径.
边心距是正多边形的中心到正多边形一边的距离，此时的边心距也可以看作正多边形的外接圆的圆心到多边形的边(即外接圆的弦)的距离，即边心距也是弦心距，但弦心距不一定是边心距.
如图所示，△AOB是正三角形，以点O为圆心，OA为半径作☉O，直径FC//AB，AO,BO的延长线分别交☉O于点D,E.求证：六边形ABCDEF为圆内接正六边形.
例 有一个亭子，它的地基是半径为4 m的正六边形，求地基的周长和面积 (结果保留小数点后一位).
过点O作OP⊥BC于P.
正n边形的中心角怎么计算？
正n边形的边长a，半径R，边心距r之间有什么关系？
边长为a，边心距为r的正n边形的面积如何计算？
2.若已知正n边形的边长、周长、边心距、面积中的任意一项，则可求出其他各项.
3.正n边形的半径和边心距把正n边形分成2n个全等的直角三角形，所以在进行与正多边形有关的计算时，可以把正多边形的计算转化到直角三角形中，利用勾股定理等知识解决.
4.由正多边形的内角与外角互补，正多边形的中心角等于外角，可得正多边形的中心角和内角互补.
2.作边心距，构造直角三角形.
1.连半径，得中心角；
圆内接正多边形的辅助线
已知边长为4的等边三角形ABC,求△ABC的中心角、半径、边心距、面积.
下列圆的内接正多边形中，一条边所对的圆心角最大的图形是( )
A.正三角形B.正方形C.正五边形D.正六边形
解：∵正三角形一条边所对的圆心角是360°÷3=120°，正方形一条边所对的圆心角是360°÷4=90°，正五边形一条边所对的圆心角是360°÷5=72°，正六边形一条边所对的圆心角是360°÷6=60°，∴一条边所对的圆心角最大的图形是正三角形.
添加辅助线的方法：连半径，作边心距
（达州中考）以半径为2的圆的内接正三角形、正方形、正六边形的边心距为三边作三角形，则该三角形的面积是( )