



专题44 巧妙设点研究圆锥曲线问题-2021年高考数学微专题复习(新高考地区专用)练习
展开一、题型选讲
题型一 、巧妙设点,降低运算量
例1、(2018南京、盐城一模)如图,在平面直角坐标系xOy中,椭圆C:eq \f(x2,a2)+eq \f(y2,b2)=1(a>b>0)的下顶点为B,点M,N是椭圆上异于点B的动点,直线BM,BN分别与x轴交于点P,Q,且点Q是线段OP的中点.当点N运动到点eq \b\lc\(\rc\)(\a\vs4\al\c1(\r(3),\f(\r(3),2)))处时,点Q的坐标为eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(2\r(3),3),0)).
(1) 求椭圆C的标准方程;
(2) 设直线MN交y轴于点D,当点M,N均在y轴右侧,且eq \(DN,\s\up6(→))=2eq \(NM,\s\up6(→))时,求直线BM的方程.
例2、(2018南京学情调研)如图,已知椭圆eq \f(x2,a2)+eq \f(y2,b2)=1(a>b>0)的离心率e=eq \f(\r(2),2),一条准线方程为x=2.过椭圆的上顶点A作一条与x轴,y轴都不垂直的直线交椭圆于另一点P,P关于x轴的对称点为Q.
(1) 求椭圆的方程;
(2) 若直线AP,AQ与x轴交点的横坐标分别为m,n,求证:mn为常数,并求出此常数.
题型二、设而不求法,降低运算量
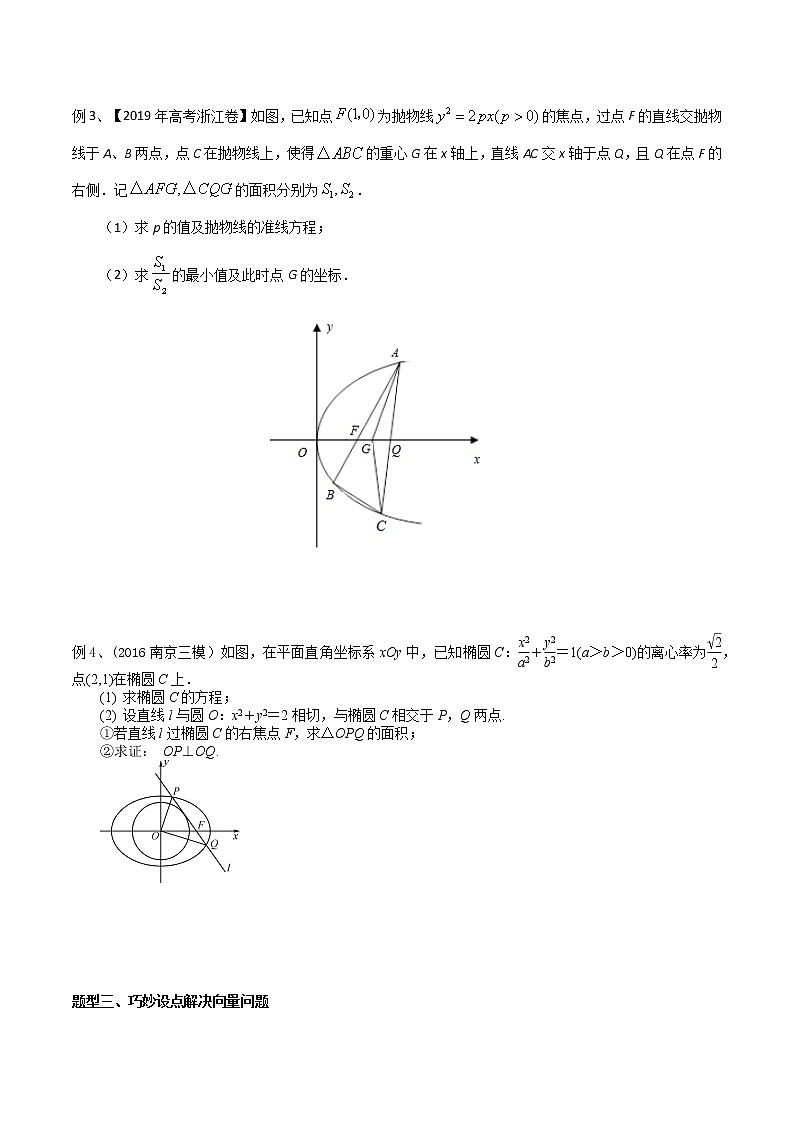
例3、【2019年高考浙江卷】如图,已知点为抛物线的焦点,过点F的直线交抛物线于A、B两点,点C在抛物线上,使得的重心G在x轴上,直线AC交x轴于点Q,且Q在点F的右侧.记的面积分别为.
(1)求p的值及抛物线的准线方程;
(2)求的最小值及此时点G的坐标.
例4、(2016南京三模)如图,在平面直角坐标系xOy中,已知椭圆C:eq \f(x2,a2)+eq \f(y2,b2)=1(a>b>0)的离心率为eq \f(\r(2),2),点(2,1)在椭圆C上.
(1) 求椭圆C的方程;
(2) 设直线l与圆O:x2+y2=2相切,与椭圆C相交于P,Q两点.
①若直线l过椭圆C的右焦点F,求△OPQ的面积;
②求证: OP⊥OQ.
题型三、巧妙设点解决向量问题
例5、(2016南通、扬州、淮安、宿迁、泰州二调)如图,在平面直角坐标系xOy中,已知椭圆eq \f(x2,a2)+eq \f(y2,b2)=1(a>b>0)的离心率为eq \f(\r(2),2).A为椭圆上异于顶点的一点,点P满足=2.
(1) 若点P的坐标为(2,eq \r(2)),求椭圆的方程;
(2) 设过点P的一条直线交椭圆于B,C两点,且=m,直线OA,OB的斜率之积为-eq \f(1,2),求实数m的值.
题型四、抛物线的特殊设点技巧
例6、【2018年高考浙江卷】如图,已知点P是y轴左侧(不含y轴)一点,抛物线C:y2=4x上存在不同的两点A,B满足PA,PB的中点均在C上.
(1)设AB中点为M,证明:PM垂直于y轴;
(2)若P是半椭圆x2+=1(x<0)上的动点,求△PAB面积的取值范围.
二、达标训练
1、【2020年高考全国Ⅰ卷理数】已知A、B分别为椭圆E:(a>1)的左、右顶点,G为E的上顶点,,P为直线x=6上的动点,PA与E的另一交点为C,PB与E的另一交点为D.
(1)求E的方程;
(2)证明:直线CD过定点.
2、(2020届山东省潍坊市高三上学期统考)已知椭圆的左、右焦点分别为,,过点的直线与椭圆交于两点,延长交椭圆于点,的周长为8.
(1)求的离心率及方程;
(2)试问:是否存在定点,使得为定值?若存在,求;若不存在,请说明理由.
3、【2019年高考全国Ⅱ卷理数】已知点A(−2,0),B(2,0),动点M(x,y)满足直线AM与BM的斜率之积为−.记M的轨迹为曲线C.
(1)求C的方程,并说明C是什么曲线;
(2)过坐标原点的直线交C于P,Q两点,点P在第一象限,PE⊥x轴,垂足为E,连结QE并延长交C于点G.
(i)证明:是直角三角形;
(ii)求面积的最大值.
4、(2016南京、盐城一模)如图,在平面直角坐标系xOy中,设点M(x0,y0)是椭圆C:eq \f(x2,4)+y2=1上的一点,从原点O向圆M:(x-x0)2+(y-y0)2=r2作两条切线分别与椭圆C交于点P,Q,直线OP,OQ的斜率分别记为k1,k2.
(1) 若圆M与x轴相切于椭圆C的右焦点,求圆M的方程;
(2) 若r=eq \f(2\r(5),5).
①求证:k1k2=-eq \f(1,4);
②求OP·OQ的最大值.
专题44 巧妙设点研究圆锥曲线问题-2022年高考数学微专题复习(新高考地区专用): 这是一份专题44 巧妙设点研究圆锥曲线问题-2022年高考数学微专题复习(新高考地区专用),文件包含专题44巧妙设点研究圆锥曲线问题解析版docx、专题44巧妙设点研究圆锥曲线问题原卷版docx等2份试卷配套教学资源,其中试卷共20页, 欢迎下载使用。
2022高考数学一轮复习专题44 巧妙设点研究圆锥曲线问题(原卷): 这是一份2022高考数学一轮复习专题44 巧妙设点研究圆锥曲线问题(原卷),共5页。试卷主要包含了题型选讲,设而不求法,降低运算量,巧妙设点解决向量问题,抛物线的特殊设点技巧等内容,欢迎下载使用。
2022高考数学一轮复习专题44 巧妙设点研究圆锥曲线问题(解析卷): 这是一份2022高考数学一轮复习专题44 巧妙设点研究圆锥曲线问题(解析卷),共15页。试卷主要包含了题型选讲,设而不求法,降低运算量,巧妙设点解决向量问题,抛物线的特殊设点技巧等内容,欢迎下载使用。












