初中数学北师大版八年级下册3 公式法优秀ppt课件

这是一份初中数学北师大版八年级下册3 公式法优秀ppt课件，共17页。PPT课件主要包含了因式分解的定义，提公因式法，3公式法，第四章因式分解，整式乘法公式，因式分解公式，1x2+y2，2x2-y2，4-x2-y2，3-x2+y2等内容，欢迎下载使用。

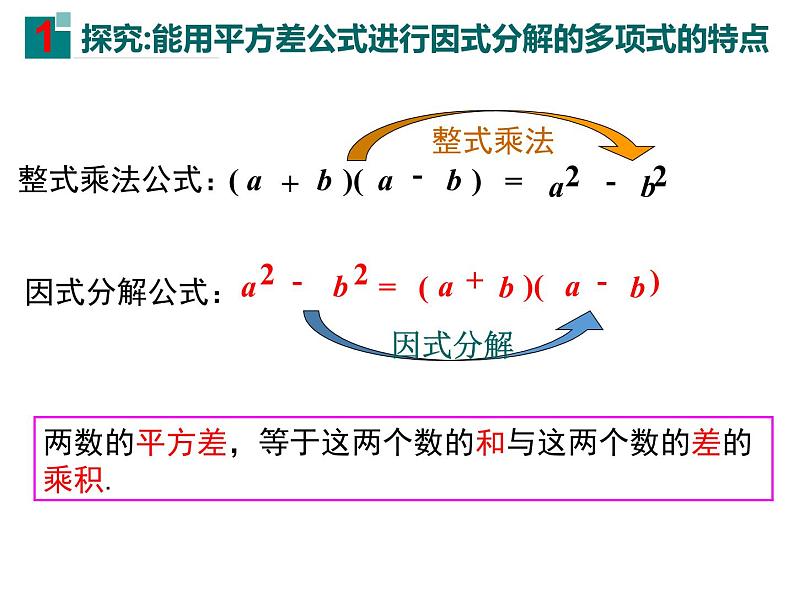
2.因式分解与整式乘法的关系：
是互为相反的变形（互逆的）
想一想：多项式x2-25, 9x2-y2能用提公因式法分解因式吗？如果不能，你有其他方法将它分解因式吗？
第1课时 平方差公式
1、探究能用平方差公式进行因式分解的多项式的特点；2、会用平方差公式进行分解因式；3、会综合运用提公因式法和平方差公式法分解因式.
两数的平方差，等于这两个数的和与这两个数的差的乘积.
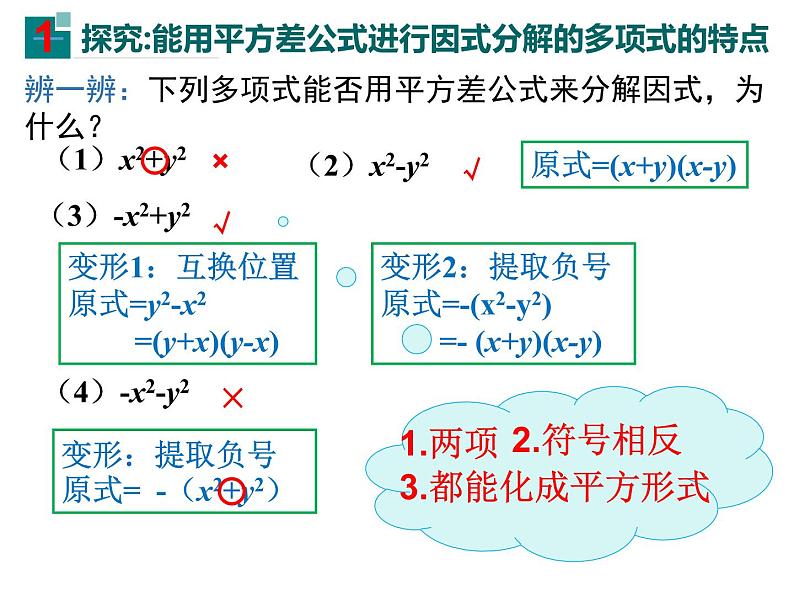
辨一辨：下列多项式能否用平方差公式来分解因式，为什么？
变形1：互换位置原式=y2-x2 =(y+x)(y-x)
原式=(x+y)(x-y)
变形2：提取负号原式=-(x2-y2) =- (x+y)(x-y)
变形：提取负号原式= -（x2+y2）
（2）9x2 - y2
【例1】利用平方差公式分解因式： （A）16m2–9n2 （B）16–x2y2 （C）25a2– （D）
法1：互换位置原式=x2-9 =(x+3)(x-3)
法2：提取负号原式= -(9-x2) = - (3+x)(3-x)
用平方差公式进行因式分解
【例2】把下列各式分解因式 （1）
（2）-16
想一想：多项式 (x+p) 2 - (x+q) 2能用平方差公式分解因式吗？
=（x+p+x+q)×(x+p-x-q）
=（2x+p+q)(p-q）
解：原式=[( )+( )]×[( )-( )]
【例3】把下列各式分解因式 （1） 9(x–y）2–（x+y）2 （2）
解:原式=[3(x-y)] 2-(x+y) 2=[3(x-y)+(x+y)][3(x-y)-(x+y)]=(3x-3y+x+y)(3x-3y-x-y)=(4x-2y)(2x-4y)=2(2x-y)×2(x-2y)=4(2x-y)(x-2y)
原式=(a-b) 2-[4(a+b)] 2=[(a-b)+4(a+b)][(a-b)-4(a+b)]=(a-b +4a+4b) (a-b -4a-4b)=(5a+3b)(-3a-5b)=-(5a+3b)(3a+5b)
综合两种方法进行因式分解
解：原式=2x(x2-4)
=2x(x+2)(x-2)
解：原式=3xy(x2-4) =3xy(x2-22) =3xy(x+2)(x-2)
解：原式=3a(x2-y4) =3a[x2-(y2)2] =3a(x+y2)(x-y2)
解：原式=32－2(m－n)2 =2[16-(m－n)2] =2[42-(m－n)2] = 2[4+(m－n)][4-(m－n)] = 2(4+m－n)(4-m+n)
a2-b2=(a+b)(a-b)（特点）
一提公因式；二套公式；三检查结果.
综合运用提公因式法和公式法分解因式
(1)书写规范：单项式在前，多项式在后；相同因式写成“幂”的形式(2)分解彻底：括号里首项不能为负;不能含有公因式 ;不能是公式
(1)改写成平方形式(系数也要改写）； (2)套用公式.
1.下列多项式中能用平方差公式分解因式的是(　　)A．a2＋(－b)2 B．5m2－20mnC．－x2－y2 D．－x2＋9
2.分解因式(2x+3)2 -x2的结果是（　　）A．3(x2+4x+3) B．3(x2+2x+3)C．(3x+3)(x+3) D．3(x+1)(x+3)
3.若a+b=3，a-b=7，则b2-a2的值为（　）
A．-21 B．21 C．-10 D．10
原式=(b+a)(b-a)
b+a=3，b-a=-7
4.计算下列各题：(1)1012－992 (2)53.52×4-46.52×4.
解：(1)原式＝(101＋99)(101－99)＝400；
(2)原式＝4(53.52－46.52)
=4(53.5＋46.5)(53.5－46.5)
＝4×100×7=2800