




专题19 立体几何综合-2020年高考数学(文)母题题源解密(全国Ⅲ专版)
展开专题19 立体几何综合
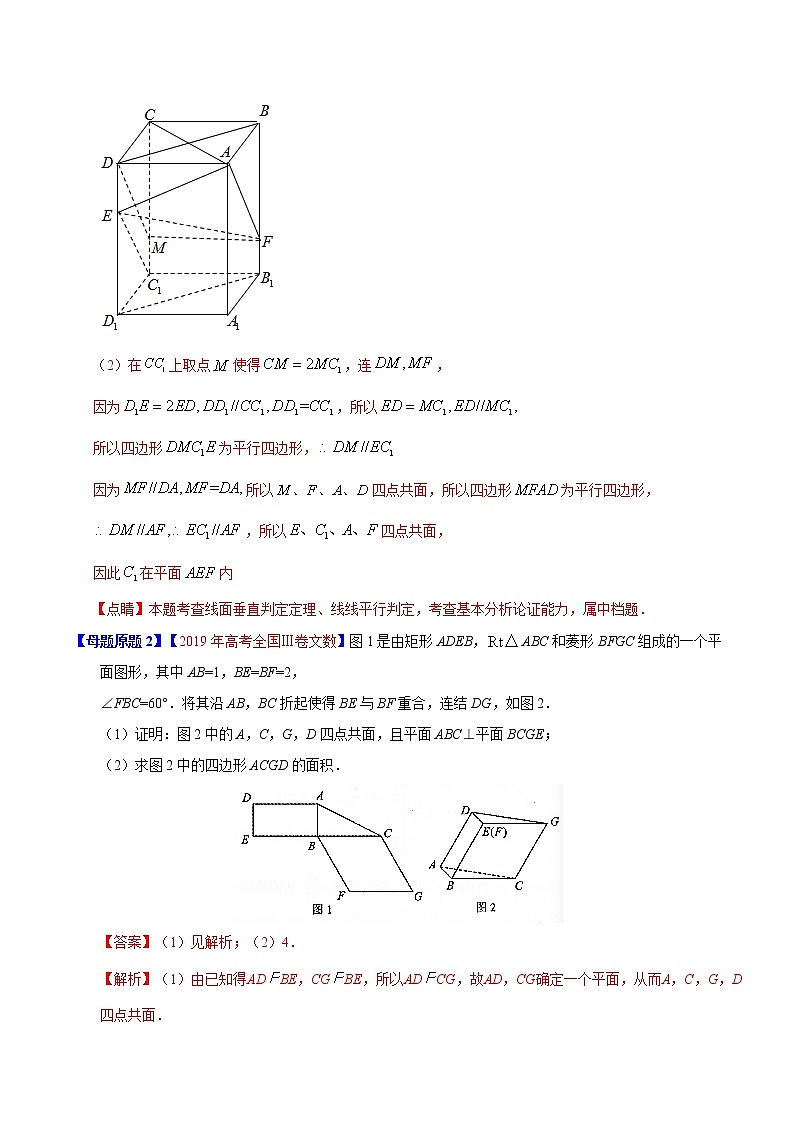
【母题原题1】【2020年高考全国Ⅲ卷,文数】如图,在长方体中,点,分别在棱,上,且,.证明:
(1)当时,;
(2)点在平面内.
【答案】(1)证明见解析;(2)证明见解析.
【解析】
【分析】
(1)根据正方形性质得,根据长方体性质得,进而可证平面,即得结果;
(2)只需证明即可,在上取点使得,再通过平行四边形性质进行证明即可.
【详解】(1)因为长方体,所以平面,
因为长方体,所以四边形为正方形
因为平面,因此平面,
因为平面,所以;
(2)在上取点使得,连,
因为,所以
所以四边形为平行四边形,
因为所以四点共面,所以四边形为平行四边形,,所以四点共面,
因此在平面内
【点睛】本题考查线面垂直判定定理、线线平行判定,考查基本分析论证能力,属中档题.
【母题原题2】【2019年高考全国Ⅲ卷文数】图1是由矩形ADEB,ABC和菱形BFGC组成的一个平面图形,其中AB=1,BE=BF=2,
∠FBC=60°.将其沿AB,BC折起使得BE与BF重合,连结DG,如图2.
(1)证明:图2中的A,C,G,D四点共面,且平面ABC⊥平面BCGE;
(2)求图2中的四边形ACGD的面积.
【答案】(1)见解析;(2)4.
【解析】(1)由已知得ADBE,CGBE,所以ADCG,故AD,CG确定一个平面,从而A,C,G,D四点共面.
由已知得ABBE,ABBC,故AB平面BCGE.
又因为AB平面ABC,所以平面ABC平面BCGE.
(2)取CG的中点M,连结EM,DM.
因为AB∥DE,AB平面BCGE,所以DE平面BCGE,故DECG.
由已知,四边形BCGE是菱形,且∠EBC=60°得EMCG,故CG平面DEM.
因此DMCG.
在DEM中,DE=1,EM=,故DM=2.
所以四边形ACGD的面积为4.
【名师点睛】本题是很新颖的立体几何考题,首先是多面体折叠问题,考查考生在折叠过程中哪些量是不变的,再者折叠后的多面体不是直棱柱,突出考查考生的空间想象能力.
【母题原题3】【2018年高考全国Ⅲ卷文数】如图,矩形所在平面与半圆弧所在平面垂直,是上异于,的点.
(1)证明:平面平面;
(2)在线段上是否存在点,使得平面?说明理由.
【答案】(1)见解析;(2)存在,理由见解析.
【解析】(1)由题设知,平面CMD⊥平面ABCD,交线为CD.
因为BC⊥CD,BC平面ABCD,
所以BC⊥平面CMD,故BC⊥DM.
因为M为上异于C,D的点,且DC为直径,所以DM⊥CM.
又BC∩CM=C,所以DM⊥平面BMC.
而DM平面AMD,故平面AMD⊥平面BMC.
(2)当P为AM的中点时,MC∥平面PBD.
证明如下:连结AC交BD于O.
因为ABCD为矩形,所以O为AC中点.
连结OP,因为P为AM 中点,所以MC∥OP.
MC平面PBD,OP平面PBD,所以MC∥平面PBD.
【名师点睛】本题主要考查面面垂直的证明,利用线线垂直得到线面垂直,再得到面面垂直,第二问先断出P为AM中点,然后作辅助线,由线线平行得到线面平行,考查学生空间想象能力,属于中档题.
【命题意图】用向量方法解决直线与直线、直线与平面、平面与平面的夹角的计算问题,了解向量方法在研究立体几何问题中的应用.主要考查考生的直观想象能力、数学运算能力、逻辑推理能力,以及转化与化归思想的应用.
【命题规律】立体几何解答题第1问主要集中考查空间中直线、平面的位置关系的判断,注重对公理、定理的考查,而第2问多考查空间向量在空间立体几何中的应用,在证明与计算中一般要用到初中平面几何的重要定理,空间思维要求较高,运算量较大,对学生的空间想象能力、转化能力、计算能力要求较高.在考查考生运算求解能力的同时侧重考查考生的空间想象能力和推理论证能力,给考生提供了从不同角度去分析问题和解决问题的可能,体现了立体几何教学中课程标准对考生的知识要求和能力要求,提升了对考生的数学能力和数学素养的考查.本试题能准确把握相关几何元素之间的关系,把推理论证能力、空间想象能力等能力和向量运算、二面角作图、建立空间直角坐标系等知识较好地融入试题中,使考生的空间想象能力、推理论证能力和运算求解能力得到了有效考查.
【答题模板】
1.一个平面的法向量是与平面垂直的向量,有无数多个,任意两个都是共线向量.
若要求出一个平面的法向量的坐标,一般要建立空间直角坐标系,然后用待定系数法求解,一般步骤如下:
(1)设平面的法向量为n=(x,y,z);
(2)找出(求出)平面内的两个不共线的向量的坐标a=(a1,b1,c1),b=(a2,b2,c2);
(3)根据法向量的定义建立关于x,y,z的方程组
(4)解方程组,取其中的一组解,即得法向量.
注意:求平面的法向量时,建立的方程组有无数组解,利用赋值法,只要给x,y,z中的一个变量赋一特殊值(常赋值–1,0,1),即可确定一个法向量,赋值不同,所求法向量不同,但n=(0,0,0)不能作为法向量.
2.用空间向量解决立体几何问题的步骤如下:
(1)建系:根据题中的几何图形的特征建立适当的空间直角坐标系;
(2)定坐标:确定点的坐标进而求出有关向量的坐标;
(3)向量运算:进行相关的空间向量的运算;
(4)翻译:将向量中的语言“翻译”成相应的立体几何中的语言,完成几何问题的求解.
【方法总结】
1.利用向量法证明平行问题
(1)证明线线平行:证明两条直线的方向向量共线.
(2)证明线面平行:
①证明该直线的方向向量与平面的某一法向量垂直;
②证明该直线的方向向量与平面内某直线的方向向量平行;
③证明该直线的方向向量可以用平面内的两个不共线的向量线性表示.
(3)证明面面平行:
①证明两个平面的法向量平行;
②转化为线线平行、线面平行问题.
注意:用向量法证明平行问题时,要注意解题的规范性.如证明线面平行时,仍需要说明一条直线在平面内,另一条直线在平面外.
2.利用向量法证明垂直问题
(1)证明线线垂直:
证明两直线的方向向量垂直,即证它们的数量积为零.
(2)证明线面垂直:
①证明直线的方向向量与平面的法向量共线;
②证明直线与平面内的两条相交直线的方向向量垂直;
③证明直线的方向向量与平面α内的任一条直线的方向向量垂直.
(3)证明面面垂直:
①其中一个平面与另一个平面的法向量平行;
②两个平面的法向量垂直.
3.求线面角
(1)定义法:①作,在斜线上选取恰当的点向平面引垂线,在这一步上确定垂足的位置是关键;
②证,证明所作的角为直线与平面所成的角,其证明的主要依据是直线与平面所成角的概念;
③求,构造角所在的三角形,利用解三角形的知识求角.
(2)公式法:sinθ=(其中h为斜线上除斜足外的任一点到所给平面的距离,l为该点到斜足的距离,θ为斜线与平面所成的角).
(3)向量法:sinθ=|cos<,n>|=(其中AB为平面α的斜线,n为平面α的法向量,θ为斜线AB与平面α所成的角).
4.求二面角
(1)定义法:在二面角的棱上找一特殊点,过该点在两个半平面内分别作垂直于棱的射线,如图(1),∠AOB为二面角α–l–β的平面角;
(2)垂面法:过棱上一点作棱的垂直平面,该平面与二面角的两个半平面的交线所形成的角即二面角的平面角,如图(2),∠AOB为二面角α–l–β的平面角;
(3)垂线法(三垂线定理法):过二面角的一个半平面内一点作另一个半平面所在平面的垂线,从垂足出发向棱引垂线,利用三垂线定理(线面垂直的性质)即可找到所求二面角的平面角或其补角,如图(3),∠AOB为二面角α–l–β的平面角;
(4)利用射影面积公式:cosθ=,该法主要用来解决无棱二面角大小的计算,关键在于找出其中一个半平面内的多边形在另一个半平面内的射影;
(5)向量法:利用公式cos
如图(2)(4)中
5.求空间距离
(1)直接法:利用线线垂直、线面垂直、面面垂直等性质定理与判定定理,作出垂线段,再通过解三角形求出距离.
(2)间接法:利用等体积法、特殊值法等转化求解.
(3)向量法:空间中的距离问题一般都可转化为点到平面的距离问题进行求解.
求点P到平面α的距离的三个步骤:
①在平面α内取一点A,确定向量的坐标;
②确定平面α的法向量n;
③代入公式d=求解.
1.(2020·西藏自治区高三二模(文))如图,三棱锥中,,,,,.
(1)求证:;
(2)求点到平面的距离.
【答案】(1)证明见解析(2)
【解析】
【分析】(1)取的中点为,连接,,证明,,推出平面,即可证明;
(2)在直角三角形中,由,为的中点,得,求解,结合,可得,又,得到平面,然后利用等体积法求点到平面的距离.
【详解】(1)证明:取的中点为,连接,.
在中,,为的中点,,
在中,,为的中点,,
,,平面,平面,
平面,;
(2)在直角三角形中,由,为的中点,得,
在等腰三角形中,由,得,
又,,即,
又,,平面,
求解三角形可得,又,得.
设点到平面的距离为,
由,得,
解得,
故点到平面的距离为.
【点睛】本题考查等体积法的应用,直线与平面垂直的判定定理的应用,考查空间想象能力以及计算能力,是中档题.
2.(2020·西藏自治区拉萨中学高一期中)(本小题满分12分)如图在四棱锥中,底面是边长为的正方形,侧面底面,且,设,分别为,的中点.
(1)求证:平面;
(2)求证:面平面.
【答案】(1)详见解析;(2)详见解析.
【解析】试题分析:(1)连结,设,从而可证在中//,根据线面平行的判定,即可得证;(2)根据题意可证得,,从而根据线面垂直的判定可知面,再由面面垂直的判定即可得证.
试题解析:(1)为平行四边形,连结,设,为中点,为中点,
∴在中,且平面,平面,∴平面;(2)∵平面平面,平面面,四边形为正方形,,平面,∴平面,∴,又∵,∴是等腰直角三角形,且即,,且,面,面,又∵面,∴平面平面.
考点:1.线面平行的判定;2.线面垂直的判定.
3.(2020·西藏自治区拉萨中学高三月考(文))如图所示,在四棱锥中,四边形为矩形,为等腰三角形,,平面平面,且,,,分别为,的中点.
(1)证明:平面;
(2)证明:平面平面;
(3)求四棱锥的体积.
【答案】(1)证明见解析;(2)证明见解析;(3).
【解析】
【分析】(1)根据直线与平面平行的判定定理可知只需证与平面内一直线平行,连接,根据中位线可知,平面,平面,即可证明结论;
(2)根据面面垂直的性质可得平面,又平面,即可证明结论;
(3)取的中点为,连接,从而得到平面,即为四棱锥的高,最后根据棱锥的体积公式即可得解.
【详解】(1)如图所示,连接.
∵四边形为矩形且是的中点,
∴也是的中点.
又是的中点,,
∵平面,平面,∴平面;
(2)证明:∵面平面,,平面平面,
∴平面,
∵平面,∴平面平面;
(3)取的中点为,连接,
∵平面平面,为等腰直角三角形,
∴平面,即为四棱锥的高,
∵,∴,又,
∴四棱锥的体积.
【点睛】本题主要考查线面平行、面面垂直的证明,考查椎体体积的求法,考查逻辑推理能力和运算能力,考查空间想象能力,属于常考题.
4.(2020·云南省高三其他(文))如图,长方体的侧面是正方形.
(1)证明:平面;
(2)若,,求点到平面的距离.
【答案】(1)证明见解析;(2)
【解析】
【分析】(1)先证明和,平面即得证;
(2)设点到平面的距离为,根据即得点到平面的距离.
【详解】(1)证明:如图1,在长方体中,
平面,
又平面,
.
四边形是正方形,
.
又,平面.
(2)解:如图2,设点到平面的距离为.
由题知,,
在长方体中,
平面,且,
,
在中,,,,
,
,,
点到平面的距离为.
【点睛】本题主要考查空间线面垂直的证明,考查空间点到平面距离的计算,意在考查学生对这些知识的理解掌握水平.
5.(2020·云南省高三其他(文))如图所示,平面平面,四边形是边长为的正方形,,分别是的中点.
(1)证明:平面;
(2)若,求四棱锥的体积.
【答案】(1)证明见解析;(2)
【解析】
【分析】(1)首先取线段的中点,连接,,根据三角形中位线的性质得到四边形为平行四边形,从而得到∥,再利用线面平行的判定即可证明.
(2)首先过作,垂足为,利用面面垂直的性质得到平面,即为四棱锥的高,再计算四棱锥的体积即可.
【详解】(1)取线段的中点,连接,.
,分别为,的中点,
则∥且.
在正方形中,∵是的中点,
∴∥且.
∴∥,且,则四边形为平行四边形,
∴∥.
∵平面,平面,
∴∥平面.
(2)过作,垂足为.
∵平面平面,平面平面,
平面,
∴平面.
又,,
所以,四棱锥的高,
故,四棱锥的体积为:.
【点睛】本题第一问考查直线与平面平行的证明,第二问考查四棱锥的体积,同时考查面面垂直的性质,属于中档题.
6.(2020·云南省高三其他(文))如图,在多边形中(图1).四边形为长方形,为正三角形,,,现以为折痕将折起,使点在平面内的射影恰好是的中点(图2).
(1)证明:平面:
(2)若点在线段上,且,求二面角的余弦值.
【答案】(1)见解析(2)
【解析】
【分析】(1)过点作,垂足为,由于点在平面内的射影恰好是中点,
可得平面,进一步得到,
又因为,,则平面;
(2)取的中点,以为坐标原点,以,,分别为、、轴的正方向建立空间直角坐标系,分别求出平面和平面的法向量,代入夹角公式可求出结果.
【详解】(1)作的中点,连接,由题知平面.
因为,所以,
又因为,
所以平面.
(2)取的中点,连接,
则,,,
以为坐标原点,以,,分别为、、轴的正方向建立空间直角坐标系.
则,,
,,
,
设平面的一个法向量为
则有,令,所以
易知平面的一个法向量为
所以,
所以二面角的余弦值为.
【点睛】本题主要考查线面垂直的判定二面角的求解,属于中档题.
7.(2020·云南省高三三模(文))已知四棱锥中,底面为正方形,为正三角形,是的中点,过的平面平行于平面,且平面与平面的交线为,与平面的交线为.
(1)在图中作出四边形(不必说出作法和理由);
(2)若,四棱锥的体积为,求点到平面的距离.
【答案】(1)见解析;(2)
【解析】
【分析】(1)根据面面平行的判定定理,取中点,中点,中点,即可得到所求四边形;
(2)由已知可证得平面,进而可证得平面,由体积公式可求得边长,因为,借助等体积转换即可求得到平面的距离,即为结果.
【详解】解:(1)如图,四边形即为所求,其中为中点,为中点,为中点.
(2)连接,
依题意:,所以,
则,又因为且,
所以平面,则,
因为为正三角形且为中点,
所以平面.
设,则,解得,
则,,
所以,
设到平面的距离为,,
所以,解得,
即点到平面的距离为.
【点睛】本题考查面面平行的判定方法,考查等体积转换求点到面的距离,考查空间想象能力和计算能力,属于中档题.
8.(2020·云南省高三一模(文))已知三棱柱,底面为等边三角形,侧棱平面,为中点,,和交于点.
(1)证明:平面;
(2)若,求点到平面的距离.
【答案】(1)证明见解析(2)
【解析】
【分析】(1)取中点,连结、,证明四边形为平行四边形,从而得到,即可得证平面;
(2)设点到平面的距离为,采用等体积法由解方程得即可.
【详解】(1)证明:取中点,连结、,
在四边形中,为中点,为中点,
所以为中位线,
故:且,
因为为中点,
所以且,
所以且,所以四边形为平行四边形,
所以,且平面,
所以平面.
(2)因为为等边三角形,为中点,,,
所以,
所以:,又因为,
所以:,.
点到平面的距离为,
设点到平面的距离为,
由得,
解得.
【点睛】本题主要考查了直线与平面平行的证明,点到平面的距离计算,考查学生采用等体积法求点到平面的距离,考查了学生直观想象能力和转化与化归的思想.
9.(2020·宜宾市叙州区第二中学校高三三模(文))如图,四棱锥中,平面,,,,为线段上一点,,为的中点.
(I)证明平面;
(II)求四面体的体积.
【答案】(Ⅰ)证明见解析;(Ⅱ).
【解析】试题分析:(Ⅰ)取的中点,然后结合条件中的数据证明四边形为平行四边形,从而得到,由此结合线面平行的判断定理可证;(Ⅱ)由条件可知四面体N-BCM的高,即点到底面的距离为棱的一半,由此可顺利求得结果.
试题解析:(Ⅰ)由已知得,取的中点,连接,由为中点知,.
又,故平行且等于,四边形为平行四边形,于是.
因为平面,平面,所以平面.
(Ⅱ)因为平面,为的中点,
所以到平面的距离为.
取的中点,连结.由得,.
由得到的距离为,故.
所以四面体的体积.
【考点】直线与平面间的平行与垂直关系、三棱锥的体积
【技巧点拨】(1)证明立体几何中的平行关系,常常是通过线线平行来实现,而线线平行常常利用三角形的中位线、平行四边形与梯形的平行关系来推证;(2)求三棱锥的体积关键是确定其高,而高的确定关键又找出顶点在底面上的射影位置,当然有时也采取割补法、体积转换法求解.
10.(2020·云南省云南师大附中高三月考(文))如图,在等腰梯形中,,,,E,F分别为,边的中点.现将沿着折叠到的位置,使得平面平面.
(1)证明:平面平面;
(2)求点B到平面的距离.
【答案】(1)见解析(2)
【解析】
【分析】(1)连接,证明是等边三角形,则,即.再利用面面垂直的性质定理即可证得结论;
(2)利用等体积法求点面距.
【详解】(1)证明:如图,连接,
∵E为的中点,故且,
故为平行四边形,.
∵,易知为等边三角形,F为的中点,
故,即.
又平面平面,且平面平面,
故平面,
又平面,
故平面平面;
(2)如图,取的中点O,连接,,
∵,∴,
平面平面,平面平面,
平面,
由(1)知平面,则,,.
设点B到平面的距离为h,
故,即,
.
【点睛】本题考查了利用面面垂直的性质定理证明线面垂直的问题,等体积法求点面距,考查了逻辑推理能力和运算能力,属于中档题.
11.(2020·云南省高三月考(文))在四棱锥中,侧面PAD是等边三角形,且平面平面ABCD,,.
(1)AD上是否存在一点M,使得平面平面ABCD;若存在,请证明,若不存在,请说明理由;
(2)若的面积为,求四棱锥的体积.
【答案】(1) 存在一点M为中点,使得平面平面ABCD,证明见详解;(2).
【解析】
【分析】(1)取中点为,根据平面,由线面垂直推证面面垂直即可;
(2)根据的面积求得各棱长度,即可由体积公式求得结果.
【详解】(1)存在点为中点,使得平面平面ABCD,证明如下:
取中点为,连接,如下图所示:
因为为等边三角形,为中点,
故可得;
又因为平面平面ABCD,且交线为,
又因为平面,,
故可得平面,又平面,
故可得平面平面,即证.
(2)不妨设,
故可得,
由(1)可知为直角三角形,
且,,
故可得;
在中,因为,
则,则,
故可得其面积,
解得;
故可得
又由(1)可知,平面,
故.
故四棱锥的体积为.
【点睛】本题考查由线面垂直推证面面垂直,以及棱锥体积的求解,属综合基础题.
12.(2020·云南省云南师大附中高三月考(文))如图,圆台的轴截面为等腰梯形,,,,圆台的侧面积为.若点C,D分别为圆,上的动点且点C,D在平面的同侧.
(1)求证:;
(2)若,则当三棱锥的体积取最大值时,求多面体的体积.
【答案】(1)证明见解析(2)
【解析】
【分析】(1)由圆台侧面积求出上下底半径,计算圆台的高,计算,由直角三角形性质得;
(2)三棱锥的高就是,表示出三棱锥的体积,求出最大值时,,多面体分为三棱锥和四棱锥,分别计算体积后相加即得.
【详解】解:(1)设,的半径分别为,,
因为圆台的侧面积为,
所以,可得.
因此,在等腰梯形中,,,.
如图,连接线段,,,
在圆台中,平面,平面,
所以.
又,所以在中,.
在中,,故,即.
(2)由题意可知,三棱锥的体积为,
又在直角三角形中,,
所以当且仅当,
即点D为弧的中点时,有最大值.
过点C作交于点M,
因为平面,平面,
所以,平面,平面,,
所以平面.
又,则点C到平面的距离,
所以四棱锥的体积.
综上,当三棱锥体积最大值时,
多面体
【点睛】本题考查多面体的体积,解题时把多面体分割成几个基本几何体,分别计算体积后相加.
13.(2020·云南省昆明一中高三月考(文))如图,三棱柱的底面是等边三角形,在底面ABC上的射影为的重心G.
(1)已知,证明:平面平面;
(2)若三棱柱的侧棱与底面所成角的正切值为,,求点到平面的距离.
【答案】(1)证明见详解,(2).
【解析】
【分析】(1)先证明和,然后得出平面即可
(2)由条件算出,,,,,然后利用求解即可.
【详解】
(1)连结并延长交于
由已知得平面,且
所以,因为,所以平面
所以
因为四边形是平行四边形,且
所以四边形是菱形,所以
因为,所以平面
因为平面,所以平面平面
(2)因为平面,所以侧棱与底面所成的角为
即
因为,所以,
因为在底面ABC上的射影为的重心G,
所以等边三角形的边长
同理,在直角三角形中,
因为在底面ABC上的射影为的重心G,
所以,且
因为,所以平面
所以,因为,所以
所以在直角三角形中,
因为,所以为直角三角形
设点到平面的距离为,由得
,所以可得
即点到平面的距离为
【点睛】求点到平面的距离常用等体积法.
14.(2020·贵州省高三其他(文))如图,在四棱锥中,为正方形,且平面平面.
(1)若点为棱的中点,在棱上是否存在一点,使得∥平面?并说明理由;
(2)若,求点到平面的距离.
【答案】(1)存在,见解析(2)
【解析】
【分析】(1)取中点,连接,可证四边形是平行四边形即可得到,从而得证;
(2)取中点,连接,可证平面,则,点到平面的距离为,由利用等体积法求点到面的距离;
【详解】解:(1)当为中点时,平面.理由如下:
如图,分别取中点,连接,又是的中点,
,
又为正方形,则,
,
又是中点,
,则四边形是平行四边形,
,又平面,平面
平面;
(2)如图,取中点,连接,又,则,
∵平面平面,平面平面平面
平面,且,
,
由(1)知,
平面,
,
在中,,
,
记点到平面的距离为,
,解得
∴点到平面的距离为
【点睛】本题考查线面平行的证明,利用等体积法求点到面的距离,属于中档题.
15.(2020·遵义市南白中学高三其他(文))如图,正方形的边长为,以为折痕把折起,使点到达点的位置,且.
(1)证明:平面平面;
(2)若是的中点,设,且三棱锥的体积为,求的值.
【答案】(1)证明见解析;(2).
【解析】
【分析】(1)要证明面面垂直,需证明线面垂直,取中点,连结,由条件证明;
(2)利用等体积转化,解得,由面积公式解得的值.
【详解】
解:(1)取中点,连结.
因为,所以.
在中,,,
则,
所以,
又,且面,
所以面,
又面,所以面面.
(2)因为面面,
又面面,且,
所以面,
所以.
又因为,,
所以.
因为,所以.
又,
所以,得.
【点睛】本题考查面面垂直的证明和利用等体积转化求参数的问题,意在考查空间想象能力和推理证明,计算能力,属于中档题型,本题第二问的关键是等体积转化,一般求四面体的体积或是求点到面的距离都需要考虑等体积转化,求点到面的距离也可以转化为其他等价的点到平面的距离.
16.(2020·贵州省高三其他(文))图是直角梯形,,,,,,点在上,,以为折痕将折起,使点到达的位置,且,如图.
证明:平面平面;
求点到平面的距离.
【答案】证明见解析;.
【解析】
【分析】在图中,连接,由已知得四边形为菱形,连接交于点,得,证明,再由线面垂直的判定可得平面,从而得到平面平面;
取的中点,连接,和,设到平面的距离为,在三棱锥中,利用,求解点到平面的距离.
【详解】解:证明:在图中,连接,由已知得,
,且,四边形为菱形,
连接交于点,,
在中,.
.
在图中,,
,.
由题意知,,且,
平面,又平面,
平面平面;
如图,取的中点,连接,和,设到平面的距离为,
在直角梯形中,为中位线,则,,
由得平面,平面,
,又,得平面,
又平面,,且.
在三棱锥中,,
即,
.
即点到平面的距离为.
【点睛】本题考查平面与平面垂直的判定,考查空间想象能力与思维能力,利用等体积法的思想,属于中档题.
17.(2020·贵州省高三其他(文))如图,四棱锥的底面是正方形,为的中点,,,,.
(1)证明:平面.
(2)求三棱锥的侧面积.
【答案】(1)证明见解析;(2).
【解析】
【分析】(1)要证明平面,只需证明,即可;
(2)只需计算,,的面积,相加即可.
【详解】(1)证明:因为为的中点,,
所以,
所以,从而.
又,,
所以底面,所以.
因为四边形是正方形,所以.
又,所以平面.
(2)由(1)知平面,因为∥,所以平面,
因为平面,所以,
所以的面积为.
易证,
所以的面积为.
故三棱锥的侧面积为.
【点睛】本题考查线面垂直的判定定理以及三棱锥侧面积的计算问题,考查学生逻辑推理能力、数学运算能力,是一道容易题.
18.(2020·贵州省高三二模(文))如图,矩形和菱形所在的平面相互垂直,为的中点.
(1)求证:平面;
(2)若,求三棱锥的体积.
【答案】(1)见解析;(2)
【解析】
【分析】(1)由已知条件,可得AB⊥AD,进一步得到AD⊥平面ABEF,则AD⊥AG,再由菱形ABEF中,∠ABE=60°,G为BE的中点,可得AG⊥BE,由线面垂直的判定定理得AG⊥平面BCE;
(2)由,得面面到面的距离等于到面的距离,,进而结合已知条件和棱锥的体积公式求解即可.
【详解】(1)证明:∵矩形和菱形所在的平面相互垂直,,∴矩形菱形,
平面,平面,∵菱形中,为的中点,
,平面
(2)由知,面面到面的距离等于到面的距离,
所以,三棱锥的体积等于三棱锥的体积,
∴矩形和菱形所在的平面相互垂直,
则,
所以,又由(1)可知平面,平面,
所以
【点睛】本题考查直线与平面垂直的判定,考查空间想象能力与思维能力,训练了利用等积法求多面体的体积,属于中档题.
19.(2020·四川省石室中学高三一模(文))如图所示,四棱柱,底面ABCD是以AB,CD为底边的等腰梯形,且,,.
(1)求证:平面平面ABCD;
(2)若,求三棱锥的体积.
【答案】(1)证明见解析;(2).
【解析】
【分析】(1)在中,利用余弦定理求出,可得,再加上,可得平面,进而可得平面平面ABCD;
(2)取BD的中点O,由(1)可得出面ABCD,通过平面ABCD,得,代入条件可得答案.
【详解】(1)中,,,,
则,
,
即,又,,
平面,
又面ABCD,所以平面平面ABCD.
(2)取BD的中点O,由于,所以,
由(1)可知平面面ABCD,而平面面,
平面,故面ABCD.
因为,,则,
因为平面ABCD,
所以
.
【点睛】本题考查面面垂直的证明,考查锥体体积的计算,关键是利用线线平行转换锥体的顶点求体积,是中档题.
20.(2020·四川省泸县第四中学高三二模(文))如图,在直四棱柱ABCD﹣A1B1C1D1中,底面ABCD是矩形,A1D与AD1交于点E,AA1=AD=2AB=4.
(1)证明:AE⊥平面ECD;
(2)求点C1到平面AEC的距离.
【答案】(1)证明见解析;(2).
【解析】
【分析】(1)由四边形ABCD是矩形,得到CD⊥AD,再由面面垂直的性质,证得CD⊥AE,结合线面垂直的判定定理,即可得到AE⊥平面ECD.;
(2)连接CD1,得到点C1到平面AEC的距离即为点C1到平面ACD1的距离, 利用“等体积法”,结合V,即可求得点C1到平面AEC的距离.
【详解】(1)∵四边形ABCD是矩形,∴CD⊥AD,
∵AA1⊥平面ABCD,CD⊂平面ABCD,∴AA1⊥CD,
又AA1∩AD=A,∴CD⊥平面ADD1A1,∴CD⊥AE,
∵四边形ADD1A1是平行四边形,∴E是A1D的中点,
∵AA1=AD,∴AE⊥DE,又CD∩DE=D,∴AE⊥平面ECD.
(2)连接CD1,则点C1到平面AEC的距离即为点C1到平面ACD1的距离,
在△ACD1中,AC=2,AD1=4,CD1=2,
∴CE⊥AD1,且CE2,
∴S4,
设C1到平面ACD1的距离为h,则V,
又V,
所以4h=16,即h,∴点C1到平面AEC的距离为.
【点睛】本题主要考查了直线与平面垂直的判定与证明,以及点到平面距离的求解,其中解答中熟记线面位置关系的判定定理和性质定理,以及熟练应用“等体积法”求解点面距是解答的关键,着重考查推理与运算能力.
21.(2020·四川省绵阳南山中学高三一模(文))如图,在直三棱柱中,,E在棱上,且,F是边的中点,G在线段上.
(1)求证:;
(2)求点F到平面的距离.
【答案】(1)证明见解析;(2).
【解析】
【分析】(1)由已知条件可证得平面,即可得由,即可证得结论;
(2)借助等体积转化,由已知求得,计算求得,进而可求得点F到平面的距离.
【详解】解:(1)如图,因为为直三棱柱,所以,
又因为,F是边的中点,
所以,
又,所以平面,
平面,所以,∴
(2)连接,在三棱锥中,,因为,
所以三角形为直角三角形,
则三棱锥高,,,
又在三角形中,,
由余弦定理,
所以,
设点F到平面的距离为h,
则由得:得,
故点F到平面的距离为.
【点睛】本题考查线面垂直的判定和性质定理,考查等体积法求点到面的距离,考查逻辑推理能力和计算能力,难度一般.
22.(2020·四川省高三二模(文))如图,在四边形中,,,,,,是的中点.现将沿翻折,使点移动至平面外的点.
(1)若,求证:平面;
(2)若平面平面,三棱锥的体积为,求线段的长.
【答案】(1)证明见解析;(2).
【解析】
【分析】(1)在线段上取靠近点的四等分点,根据长度和角度关系可证得四边形为平行四边形,结合线面平行的判定定理可证得结论;
(2)利用面面垂直性质可证得平面,采用体积桥的方式可求得,进而构造方程可求得结果.
【详解】(1),为中点,,
,,,
又,,
,,
在线段上取靠近点的四等分点,连接,,
,,
,,
四边形为平行四边形,,
又平面,平面,平面.
(2)由得:.
平面平面,平面平面,
平面,平面
由(1)知:,则,
,.
由,
解得:,.
【点睛】本小题主要考查平面与平面垂直的性质、直线与平面平行的判定、棱锥体积公式等基础知识;考査空间想象能力、运算求解能力和推理论证能力.
23.(2020·四川省仁寿第一中学校北校区高三二模(文))如图,在四棱锥中,底面为菱形,且,,.
(1)证明:平面平面;
(2)有一动点在底面的四条边上移动,求三棱锥的体积的最大值.
【答案】(1)见解析;(2)
【解析】
【分析】(1)取中点,连结,,,由已知可得为等边三角形,为等腰三角形,可得,,进而可得平面平面,由勾股定理可证,再由面面垂直的性质定理即可证得平面平面;
(2)结合图形可知当在点处,此时三棱锥的体积最大,而,故只需求三棱锥的体积即可.
【详解】
如图,取中点,连结,,,
因为,为的中点,所以,
又底面为菱形,所以,又,
所以为等边三角形,又为的中点,
所以,又,平面,
所以平面,又平面,
所以平面平面,
又在等边三角形中,,所以,
又在中,,,所以,
所以,所以,
又平面平面,平面,
所以平面,又平面,
所以平面平面.
(2)当在点处,此时三棱锥的体积最大,
因为,,,
在菱形中,,,
所以,
由(1)知平面,,
所以,
所以三棱锥的体积的最大值为.
【点睛】本题主要考查线面垂直的判定定理,面面垂直的性质定理及变换底面求三棱锥的体积,属于中档题.
24.(2020·四川省高三三模(文))如图,在多面体中,为矩形,为等腰梯形,,,,且,平面平面,,分别为,的中点.
(Ⅰ)求证:平面;
(Ⅱ)若,求多面体的体积.
【答案】(Ⅰ)证明见解析;(Ⅱ).
【解析】
【分析】(Ⅰ)取的中点.连接,,可证,,然后利用平面平面,可证平面.(Ⅱ)将多面体分为四棱锥和三棱锥两部分,将转化为,然后利用四棱锥和三棱锥的体积公式分别求出然后求和即可.
【详解】解:(Ⅰ)如图,取的中点.连接,.
在矩形中,∵,分别为线段,的中点,
∴.
又平面,平面,
∴平面.
在中,∵,分别为线段,的中点,
∴.
又平面,平面,
∴平面.
又,平面,
∴平面平面
又平面,∴平面.
(Ⅱ)如图,过点作于.
∵平面平面,平面平面,平面,
∴平面.
同理平面.
连接,.在中,∵,,
∴.
同理.
∵,∴等边的高为,即.
连接.
∴
.
【点睛】本题考查利用线线平行,线面平行和面面平行的判定定理和性质定理,考查分割法求多面体的体积,考查四棱锥和三棱锥的体积公式,考查学生的转化能力和计算能力,属于中档题.
25.(2020·四川省泸县第二中学高三二模(文))在三棱柱中,,为的中点.
(1)证明:平面;
(2)若,点在平面的射影在上,且侧面的面积为,求三棱锥的体积.
【答案】(1)见解析;(2).
【解析】
【分析】【详解】试题分析:(1)连接交于点,连接.利用中点可得,所以平面.(2)取中点,连接,过点作于,连接,利用等腰三角形和射影的概念可知平面,所以,所以平面,所以.利用侧面的面积可计算得三棱锥的高,由此可计算得三棱锥的体积.
试题解析:
(1)证明:连接交于点,连接.
则为的中点,又为的中点,所以,且平面,平面,则平面.
(2)解:取的中点,连接,过点作于点,连接.
因为点在平面的射影在上,且,
所以平面,∴,,∴平面,
则.
设,在中,,,
∴,,,
由,可得.
则
.
所以三棱锥的体积为.
26.(2020·四川省绵阳南山中学高三其他(文))如图,在直三棱柱中,,是的中点,.
(1)求证:平面;
(2)若异面直线和所成角为,求四棱锥的体积.
【答案】(1)证明见解析.(2)
【解析】
【分析】(1) 连交于点,连.再根据中位线证明即可.
(2) 根据(1)可知或其补角为异面直线和所成角,再判断可得为等边三角形,即可求得,再根据线面垂直的判定与性质可得平面,继而求得四棱锥的体积即可.
【详解】(1)证明:如图,连交于点,连.
因为直三棱柱中,四边形是矩形,故点是中点,
又是的中点,故,
又平面,平面,故平面.
(2)解:由(1)知,又,故或其补角为异面直线和所成角.
设,则,,,故为等腰三角形,故,
故为等边三角形,则有,得到.
故为等腰直角三角形,故,又平面,平面,
故,又,故平面,
又梯形的面积,,
则四棱锥的体积.
【点睛】本题主要考查了线面平行的证明以及根据异面夹角求解线段长度的方法,同时也考查了锥体体积的求法,需要根据题意确定线面垂直,找到锥体的高进而求得体积.属于中档题.
27.(2020·宜宾市叙州区第一中学校高三二模(文))如图,在中,,,,分别为,的中点是由绕直线旋转得到,连结,,.
(1)证明:平面;
(2)若,棱上是否存在一点,使得?若存在,确定点 的位置;若不存在,请说明理由.
【答案】(1)见解析(2)存在,为的中点
【解析】
【分析】(1)要证平面,则证和;证由平面几何知识可得,证,只需证,即证平面,利用线面垂直判定可得.
(2),等体积转化,由且,则可解.
【详解】(1)依题意得,
所以
因为分别为,的中点,
所以
因为
所以
又因为由沿旋转得到,
所以,平面,平面
则平面
所以,即
所以平面
解法一:(2)若,
则
因为且
所以,
又
所以为的中点
解法二:(2)因为,,,
所以,,
又,所以
由(1)知平面
若,
则,
所以
由(1)知,在中,
,即
解得
所以为正三角形,
即,所以M为的中点
【点睛】本小题主要考查空间直线与直线、直线与平面的位置关系、平面与平面位置关系,几何体的体积等基础知识,考查空间想象能力、推理论证能力、运算求解能力,考查化归与转化思想等.
28.(2020·四川省泸县五中高三二模(文))如图所示的几何体中,四边形是正方形,四边形是梯形,,且,,平面平面ABC.
(1)求证:平面平面;
(2)若,,求几何体的体积.
【答案】(1)证明见解析(2)
【解析】
【分析】(1)取BC的中点E,连接,可证明平面,根据可证明四边形为平行四边形,从而可证平面,进而证明平面平面.(2)将所求几何体分割为四棱锥和直三棱柱两部分,通过四棱锥和棱柱的体积分别计算求和可得几何体的体积.
【详解】解:(1)取BC的中点E,连接,∵,∴
∵是正方形,∴,又平面平面ABC,∴平面ABC,
又∵平面ABC,∴
又∵,平面,,∴平面
∵,∴四边形为平行四边形,∴,
∴四边形为平行四边形
∴,∴平面
又平面,∴平面平面
(2)由(1)知所求几何体为四棱锥和直三棱柱的组合体
∵,,,平面,∴平面,
∴四棱锥的体积
直三棱柱的体积
∴所求几何体的体积
【点睛】本题考查面面垂直的判定定理,考查求棱锥和棱柱的体积,考查学生数形结合的能力,属于中档题.
29.(2020·四川省棠湖中学高三一模(文))如图1,已知菱形的对角线交于点,点为线段的中点,,,将三角形沿线段折起到的位置,,如图2所示.
(Ⅰ)证明:平面平面;
(Ⅱ)求三棱锥的体积.
【答案】(Ⅰ)见证明;(Ⅱ)
【解析】
【分析】(Ⅰ)折叠前,AC⊥DE;,从而折叠后,DE⊥PF,DE⊥CF,由此能证明DE⊥平面PCF.
再由DC∥AE,DC=AE能得到DC∥EB,DC=EB.说明四边形DEBC为平行四边形.可得CB∥DE.由此能证明平面PBC⊥平面PCF.
(Ⅱ)由题意根据勾股定理运算得到,又由(Ⅰ)的结论得到 ,可得平面,再利用等体积转化有,计算结果.
【详解】(Ⅰ)折叠前,因为四边形为菱形,所以;
所以折叠后,,, 又,平面,
所以平面
因为四边形为菱形,所以.
又点为线段的中点,所以.
所以四边形为平行四边形.
所以.
又平面,所以平面.
因为平面,所以平面平面.
(Ⅱ)图1中,由已知得,,
所以图2中,,又
所以,所以
又平面,所以
又,平面,
所以平面,
所以.
所以三棱锥的体积为.
【点睛】本题考查线面垂直、面面垂直的证明,考查空间中线线、线面、面面间的位置关系等基础知识,考查了三棱锥体积的求法,运用了转化思想,是中档题.
30.(2020·四川省高三零模(文))如图,在四棱锥中,侧面底面,底面为梯形
(1)证明:;
(2)若为正三角形,求点到平面的距离.
【答案】(1)证明见解析 (2)
【解析】
【分析】(1)利用面面垂直的性质定理即可证出.
(2)取中点,连接,利用等体法:由即可求解.
【详解】(1)证明:因为,又底面为直角梯形
面底面平面
又平面
(2)因为侧面底面
为正三角形,取中点,连接
底面
设点到面的距离为
【点睛】本题主要考查了面面垂直的性质定理、等体法求点到面的距离,需熟记锥体的体积公式,考查了学生的推理能力,属于中档题.
31.(2020·宜宾市叙州区第二中学校高三一模(文))如图,在四棱锥中,平面,在四边形中,,,,,,.
(1)证明:平面;
(2)求B点到平面的距离
【答案】(1)见解析(2)
【解析】
【分析】(1)在三角形中,由勾股定理可证得,由平面,可得,根据线面垂直的判定定理即可证得结论;
(2) 在平面中,过A作BC的平行线交CD的延长线于M,因为 利用等体积转换即可求得距离.
【详解】解:(1)在平面中,,,,则,
又,
∴,即,又平面,则,又,
∴平面.
(2)在平面中,过A作BC的平行线交CD的延长线于M,
因为,,,则,又因为,,所以.
所以
又,则,所以,在中,
.
因为,则面,所以
由
可知:,,
所以,则,
因此P点到平面的距离为.
【点睛】本题考查线面垂直的判定定理,考查利用等体积转换求点到面的距离,属于中档题.
32.(2020·广西壮族自治区南宁三中高三月考(文))两个边长均为2的正方形与按如图的位置放置,为的中点,().
(1)当时,证明:平面;
(2)若在平面上的射影为的中点,与平面所成角为30°,求的值.
【答案】(1)证明见解析;(2).
【解析】
【分析】(1),是的中点,取的中点,利用面面平行得证.
(2)过作垂直于平面,垂足为,作中点,求得,,利用余弦定理求得得解.
【详解】(1)证明:如图,取的中点,的中点为,连接,,
∵,,
∴是的中点,
∴,又平面,
∴平面
同理可证,平面,又∵,
∴平面平面.
又平面,∴平面.
(2)解:过作垂直于平面,垂足为,作中点,
因为在平面上的射影为的中点,
∴,
, ,
在△中,.
由与平面所成角为30,∴.
在△中,由余弦定理得,
∴,
解得或(舍去),
∴,.
【点睛】本题考查利用面面平行证明线面平行及与空间角有关的探索性问题.
与空间角有关的探索性问题主要为与两异面直线所成的角、直线与平面所成的角和二面角有关的存在性问题,常利用空间向量法求解,求解时,一般把“是否存在”问题转化为“点的坐标是否有解,是否有规定范围内的解”等问题,并注意准确理解和熟练应用夹角公式;也可转化为利用正弦定理和余弦定理解三角形求得.
33.(2020·广西壮族自治区高三其他(文))已知四棱锥,底面为正方形,且底面,过的平面与侧面的交线为,且满足(表示的面积).
(1)证明:平面;
(2)当时,求点到平面的距离.
【答案】(1)见解析(2)
【解析】
【分析】【详解】(Ⅰ)证明:由题知四边形ABCD为正方形
∴AB//CD,又平面PCD,AB平面PCD
∴AB//平面PCD
又AB平面ABFE,平面ABFE∩平面PCD=EF
∴EF // AB,又AB//CD
∴EF //CD,
由S△PEF:S四边形CDEF=1:3知E、F分别为PC、PD的中点
连接BD交AC与G,则G为BD中点,
在△PBD中FG为中位线,∴ EG//PB
∵ EG//PB,EG平面ACE,PB平面ACE
∴PB//平面ACE.
(Ⅱ)∵PA=2,AD=AB=1, ∴,
∵CD⊥AD,CD⊥PA,AD∩PA=A,
∴CD⊥平面PAD,∴CD⊥PD
在Rt△CDE中,
在△ACE中由余弦定理知
∴,∴S△ACE=
设点F到平面ACE的距离为,则
由DG⊥AC,DG⊥PA,AC∩PA=A,得DG⊥平面PAC,且
∵E为PD中点,∴E到平面ACF的距离为
又F为PC中点,∴S△ACF S△ACP ,∴
由知
∴点F到平面ACE的距离为.
34.(2020·广西壮族自治区高三月考(文))如图,在三棱柱中,平面,,,分别是,,的中点,点在线段上,.
(1)求证:平面;
(2)若平面平面,,,求点到平面的距离.
【答案】(1)证明见解析;(2)
【解析】
【分析】(1)由,分别是,的中点,可得,再由线面平行的判定定理即可证出;
(2)根据平面平面,可得点是线段上靠近的四等分点,从而可求得,利用等体积法即可求出点到平面的距离.
【详解】(1)因为在中,,分别是,的中点,
所以,又平面,平面,
所以平面.
(2)设点到平面的距离为,点到平面的距离为,则
取的中点连结,,则,
又平面,平面,所以平面,
又平面平面,而平面,
所以平面,又平面,所以,
又为的中点,所以为的中点,
所以点是线段上靠近的四等分点,所以,
所以,,
在中,由余弦定理,得
,
所以,
在中,由余弦定理,得
,
所以,
所以,
解得,即点到平面的距离.
【点睛】本题主要考查线面平行的判定定理,等体积法求点到面的距离,属于中档题.
35.(2020·广西壮族自治区高三其他(文))如图,在四棱锥中,四边形是等腰梯形,,,,三角形是等边三角形,平面平面,、分别为、的中点.
(1)求证:平面平面;
(2)若,,求的值.
【答案】(1)见解析;(2).
【解析】
【分析】(1)利用面面垂直的性质定理得出平面,可得出,再推导出,利用线面垂直的判定定理可得出平面,再利用面面垂直的判定定理可证得结论成立;
(2)记在边上的高为,在边上的高为,计算出的值,并计算出的值,再由可求得的值.
【详解】(1)因为平面平面,平面平面,平面,,所以平面,
又因为平面,所以,
连接,
因为、分别为、的中点,所以.
因为,
所以.
又因为,
所以,
所以,所以.
又因为,所以.
又,
所以平面.
又因为平面,
所以平面平面;
(2)记在边上的高为,在边上的高为,
则,
在等腰梯形中易知,
故,
因为,所以,
所以.
【点睛】本小题主要考查平面与平面垂直的判定、平面与平面垂直的性质、三棱锥的体积、平面向量共线定理等基础知识,考查空间想象能力、运算求解能力、推理论证能力和创新意识,考查化归与转化等数学思想,属于中等题.
36.(2020·广西壮族自治区高三月考(文))如图,在四棱锥中,平面,,,且,.
(1)证明:;
(2)若,且四棱锥的体积为,求的面积.
【答案】(1)证明见解析;(2)
【解析】
【分析】(1)根据已知可得,即,再由平面可得,根据线面垂直的判定定理可得平面,从而可得;
(2)根据(1)可求得四边形的面积,由平面可知为四棱锥的高,再根据锥体的体积公式可求出,从而可求出,,由三角形面积公式即可求出答案.
【详解】(1)证明:因为,且,所以,
因为,,所以,
所以,所以,又,
所以,即.
因为平面,平面,
所以,又,,平面,
所以平面,又平面,
所以.
(2)解:由(1)可知,.
因为,
所以四边形的面积,
又,
所以,
因为平面,
所以为四棱锥的高,
所以四棱锥的体积,
解得.
因为平面,平面,所以,
又,,
所以的面积为.
【点睛】本题主要考查线面垂直的判定定理,锥体的体积公式,属于基础题.
37.(2020·广西壮族自治区田阳高中高二月考(文))如图,在三棱锥中,,分别为棱的中点,平面平面.
求证:
(1)∥平面;
(2)平面平面.
【答案】(1)详见解析;(2)详见解析.
【解析】
【分析】(1)证得MN∥BC,由线面平行的判定定理证明即可;(2)证得平面.
由面面垂直的判定定理证明即可
【详解】(1)∵分别为棱的中点,
∴MN∥BC
又平面,
∴∥平面.
(2)∵,点为棱的中点,
∴,
又平面平面,平面平面,
∴平面.
∵平面,
∴平面平面.
【点睛】本题考查线面平行,面面垂直的判定,考查定理,是基础题
38.(2020·广西壮族自治区桂平市第五中学高三月考(文))如图,在直三棱柱中,,,,,、分别为、的中点.
求证:平面;
设为上一点,且,求点到平面的距离.
【答案】证明见解析;.
【解析】
【分析】根据得,并且得出四边形为正方形,进而即可求证;
先算出点到平面的距离即为,由,可求出,设点到平面的距离为,则,进而求出点到平面的距离.
【详解】解:证明:,,
,即,
又是直三棱柱,
平面,则,
、分别为、的中点,且,,
四边形为正方形,则,
又,
平面.
由知,即,
又是直三棱柱,
平面,,
则点到平面的距离即为,
,
由知,,且,
,
设点到平面的距离为,
则
,则,
即点到平面的距离为.
【点睛】本题考查空间立体几何图形中线面垂直的判定,考查等体积法的运用,考查分析能力和运算能力,属于中档题.
39.(2020·广西壮族自治区高三其他(文))在三棱锥中,,,平面平面,点在棱上.
(1)若为的中点,证明:.
(2)若三棱锥的体积为,求到平面的距离.
【答案】(1)见解析;(2)
【解析】
【分析】(1)取的中点,连接,,根据,得到,由平面平面,得到平面,,再利用,得到,根据为的中点证明.
(2)由(1)得到,根据三棱锥的体积为,得到,再由等体积法求解.
【详解】(1)如图所示:
取的中点,连接,,
因为,所以.
又因为平面平面,且相交于,
所以平面,
所以.
因为,所以,
所以,所以,
所以,且为的中点,
所以.
(2),
所以.
在中,,
设到平面的距离为,则,
解得.
所以到平面的距离为.
【点睛】本题考查等差线线垂直,线面垂直以及等体积法求点到面的距离,还考查了转化化归的思想和逻辑推理,运算求解的能力,属于中档题.
【高考真题解密】高考数学真题题源——专题08《立体几何综合》母题解密(新高考卷): 这是一份【高考真题解密】高考数学真题题源——专题08《立体几何综合》母题解密(新高考卷),文件包含高考真题解密高考数学真题题源专题08《立体几何综合》母题解密新高考卷解析版docx、高考真题解密高考数学真题题源专题08《立体几何综合》母题解密新高考卷原卷版docx等2份试卷配套教学资源,其中试卷共40页, 欢迎下载使用。
专题16 几何体的体积-2020年高考数学(文)母题题源解密(全国Ⅲ专版): 这是一份专题16 几何体的体积-2020年高考数学(文)母题题源解密(全国Ⅲ专版),文件包含专题16几何体的体积-2020年高考数学文母题题源解密原卷版docx、专题16几何体的体积-2020年高考数学文母题题源解密解析版docx等2份试卷配套教学资源,其中试卷共48页, 欢迎下载使用。
专题21 圆锥曲线综合-2020年高考数学(文)母题题源解密(全国Ⅲ专版): 这是一份专题21 圆锥曲线综合-2020年高考数学(文)母题题源解密(全国Ⅲ专版),文件包含专题21圆锥曲线综合-2020年高考数学文母题题源解密原卷版docx、专题21圆锥曲线综合-2020年高考数学文母题题源解密解析版docx等2份试卷配套教学资源,其中试卷共110页, 欢迎下载使用。












