初中数学湘教版八年级下册2.6 菱形综合与测试课时训练

2.6菱形同步课时训练

一、单选题(共40分)

1．(本题4分)如图，矩形ABCD中，AC，BD相交于点O，过点B作BF⊥AC交CD于点F，交AC于点M，过点D作DE∥BF交AB于点E，交AC于点N，连接FN，EM．则下列结论：①DN＝BM；②EM//FN；③AE＝FC；④当AO＝AD时，四边形DEBF是菱形．其中，正确结论的个数是（　　）

A．1个 B．2个 C．3个 D．4个

2．(本题4分)将矩形纸片ABCD按如图所示的方式折叠，得到菱形AECF．若AB＝3，则BC的长为（   ）

A．1 B．2 C． D．

3．(本题4分)如图，在菱形ABCD中，对角线AC、BD交于点O，且AC＝6，BD＝8，过A点作AE垂直BC，交BC于点E，则的值为（　　）

A． B． C． D．

4．(本题4分)如图，已知菱形的顶点，且，若菱形绕点逆时针旋转，每秒旋转，则第2020秒时，菱形的对角线交点的坐标为（     ）

A． B．

C． D．

5．(本题4分)如图，菱形中，分别是的中点，若，则菱形的周长为（ ）

A．24 B．18 C．12 D．9

6．(本题4分)如图， 菱形ABCD的对角线AC，BD相交于点O，过点A作AE⊥BC于点E，连接OE．若OB=6，菱形ABCD的面积为54，则OE的长为（　　）

A．4 B．4.5 C．8 D．9

7．(本题4分)在菱形ABCD中，∠ABC=60゜，AC=4，则BD=( )

A． B．2 C．3 D．4

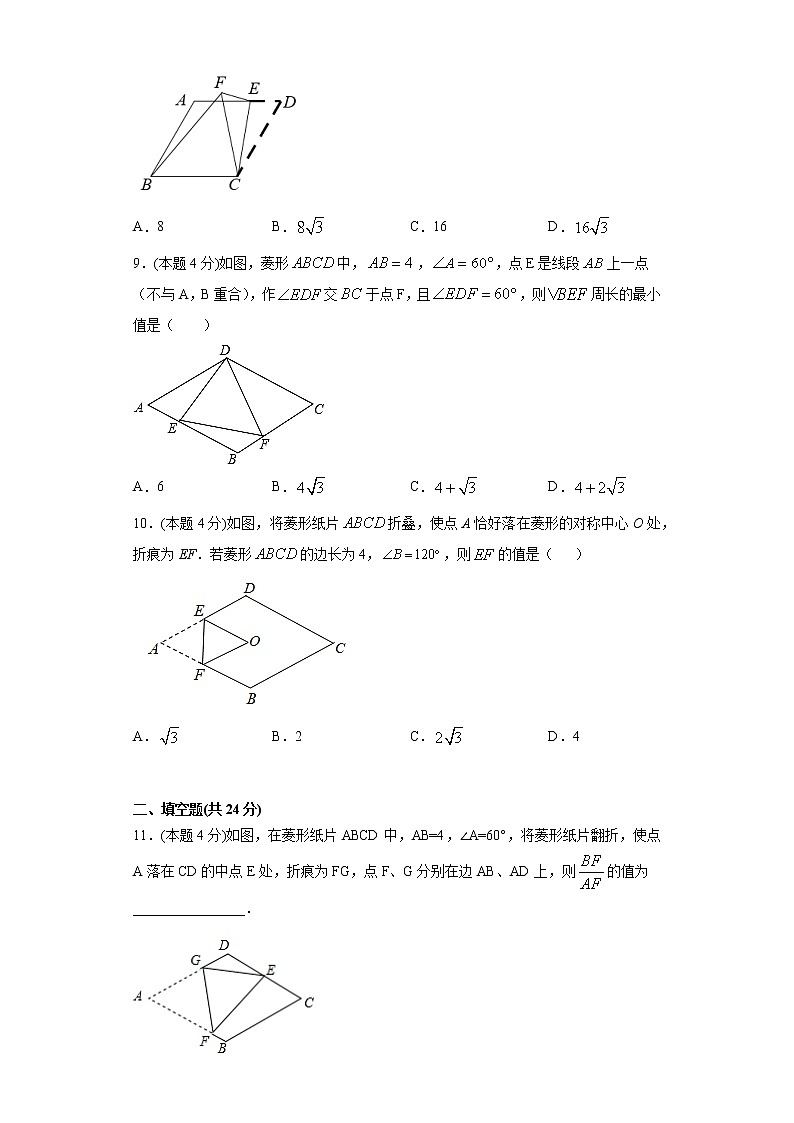
8．(本题4分)如图，菱形ABCD中，∠ABC=60°，AB=4，E是边AD上一动点，将△CDE沿CE 折叠，得到△CFE，则△BCF面积的最大值是（   ）

A．8 B． C．16 D．

9．(本题4分)如图，菱形中，，，点E是线段上一点（不与A，B重合），作交于点F，且，则周长的最小值是（    ）

A．6 B． C． D．

10．(本题4分)如图，将菱形纸片折叠，使点A恰好落在菱形的对称中心O处，折痕为EF．若菱形的边长为4，，则的值是（   ）

A． B．2 C． D．4

二、填空题(共24分)

11．(本题4分)如图，在菱形纸片ABCD中，AB=4，∠A=60°，将菱形纸片翻折，使点A落在CD的中点E处，折痕为FG，点F、G分别在边AB、AD上，则的值为________________．

12．(本题4分)如图，菱形的边长为12，，连接，，垂足为H，分别交，，的延长线于点E，M，F．若，则的长为________．

13．(本题4分)如图，在菱形ABCD中，对角线AC，BD交于点O，过点A作AH⊥BC于点H，已知BO＝4，S菱形ABCD＝24，则AH＝________．

14．(本题4分)己知菱形的边长是3，点在直线上，=1，联结与对角线相交于点，则 的值是______．

15．(本题4分)如图，菱形ABCD的对角线相交于点O，AC＝12，BD＝16，点P为边BC上一点，且P不与写B、C重合．过P作PE⊥AC于E，PF⊥BD于F，连结EF，则EF的最小值等于__________．

16．(本题4分)如图，点O是菱形ABCD对角线的交点，DEAC，CEBD，连接OE，设AC＝12，BD＝16，则OE的长为_____．

三、解答题(共36分)

17．(本题9分)在中，，是的中点，是的中点．过点作交的延长线于点．

（1）求证：≌；

（2）证明四边形是菱形．

18．(本题9分)如图，已知菱形ABCD的对角线AC、BD相交于点O，分别过A、D两点作AO、DO的垂线，两垂线交于点E．

（1）求证：四边形AODE是矩形；

（2）若四边形AODE的面积为12，AD＝5，求四边形AODE的周长．

19．(本题9分)如图，在菱形ABCD中，E为对角线BD上一点，且AE＝DE，连接CE．

（1）求证：CE＝DE．

（2）当BE＝2，CE＝1时，求菱形的边长．

20．(本题9分)如图，在直角坐标系中，四边形OABC是矩形，OA＝8，OC＝6，点D是对角线AC的中点，过点D的直线分别交OA、BC边于点E、F．

（1）求证：四边形EAFC是平行四边形；

（2）当CE＝CF时，求EF的长；

（3）在条件（2）的情况下，P为x轴上一点，当以E，F，P为顶点的三角形为等腰三角形时，请求出点P的坐标．

参考答案

1．D

2．D

3．C

4．D

5．A

6．B

7．D

8．A

9．D

10．B

11．

12．10

13．

14．或

15．4.8

16．10

17．（1）见解析；（2）见解析．

【详解】

（1）∵，

∴，

∵是中点，是边上的中线，

∴，，

在和中，

，

∴≌（AAS）．

（2）由（1）知≌，

则，

∵，

∴，

∵，

∴四边形是平行四边形，

∵，是的中点，是中点，

∴，

∴四边形是菱形．

18．（1）见解析（2）14．

【详解】

解：（1）∵四边形ABCD是菱形，
∴AC⊥BD，
∴∠AOD=90°，
∵EA⊥AO，DO⊥AO，
∴∠EAO=∠DOA=90°，
∴四边形AODE是矩形；
(2)由(1)知,四边形AODE是矩形，
∴∠AED=90°，
∵AD=5，
∵四边形AODE的面积为12，
∴AO×OD=12，
在Rt△AOD中，根据勾股定理得，
，
∴=25+24=49．

∴AO+OD=7

∴四边形AODE的周长为14

19．（1）见解析   （2）

【详解】

（1）∵四边形ABCD是菱形，

∴∠ABE＝∠CBE，AB＝CB，

在△ABE和△CBE中，

，

∴△ABE≌△CBE，

∴AE＝CE，

∵AE＝DE，

∴CE＝DE；

（2）如图，连接AC交BD于H，

∵四边形ABCD是菱形，

∴AH⊥BD，BH＝DH，AH＝CH，

∵CE＝DE＝AE＝1，

∴BD＝BE+DE＝2+1＝3，

∴BH＝BD＝，EH＝BE﹣BH＝2﹣＝，

在Rt△AHE中，由勾股定理得：AH＝＝＝，

在Rt△AHB中，由勾股定理得：AB＝＝＝，

∴菱形的边长为．

20．（1）见解析；（2）；（3）点P的坐标为（8，0）或（，0）或（﹣，0）或（，0）

【详解】

（1）证明：∵四边形OABC是矩形，

∴BC∥OA，

∴∠FCD＝∠DAE，∠CFD＝∠AED，

∵D是AC的中点，

∴CD＝AD，

∴△CDF≌△ADE（AAS），

∴DF＝DE，

∴四边形EAFC是平行四边形；

（2）解：∵四边形EAFC是平行四边形，CE＝CF，

∴四边形EAFC是菱形，

∴CE＝EA，AC⊥EF，

设CE＝AE＝x，

∵OC2+OE2＝CE2，

∴62+（8﹣x）2＝x2，

∴x＝，

∴CE＝，

∵OA＝8，OC＝6，

∴AC＝＝＝10，

∴CD＝AC＝5，

∴ED＝＝＝，

∴EF＝2ED＝；

（3）由（2）可知，，

分三种情况：

①若PE＝PF，点P与点A重合，

∴P（8，0），

②若EF＝EP＝，

当点P在x轴的正半轴上，OP＝OE+PE＝＝，

∴P（，0），

当点P在x轴的负半轴上，OP＝PE﹣OE＝＝，

∴P（﹣，0），

③若EF＝FP，过点F作FG⊥AE于点G，则EG＝CF﹣OE＝﹣＝，

∴EP＝9，

∴OP＝OE+EP＝+9＝，

∴P（，0）．

综上可得，点P的坐标为（8，0）或（，0）或（﹣，0）或（，0）．