苏科版八年级下册第11章 反比例函数11.1 反比例函数巩固练习

八下第十一章《反比例函数》难题训练（1）

                    班级：___________姓名：___________ 得分：___________

一、选择题

1. 已知点，都在反比例函数的图象上，且，则下列说法正确的是

A.  B.  C.  D. 无法确定

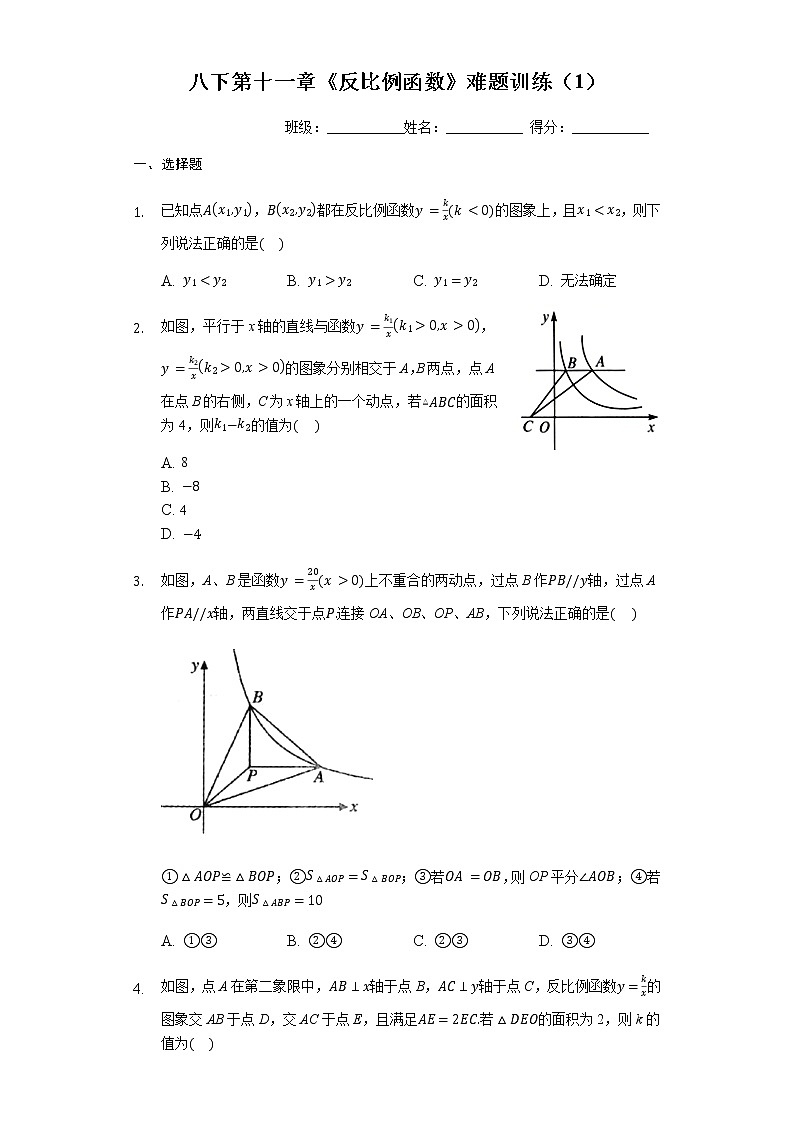
2. 如图，平行于x轴的直线与函数，的图象分别相交于A，B两点，点A在点B的右侧，C为x轴上的一个动点，若的面积为4，则的值为   

A. 8
B.
C. 4
D.

3. 如图，A、B是函数上不重合的两动点，过点B作轴，过点A作轴，两直线交于点连接OA、OB、OP、AB，下列说法正确的是   

≌；；若，则OP平分；若，则

A.  B.  C.  D.

4. 如图，点A在第二象限中，轴于点B，轴于点C，反比例函数的图象交AB于点D，交AC于点E，且满足若的面积为2，则k的值为
   
    

A.  B.  C.  D.

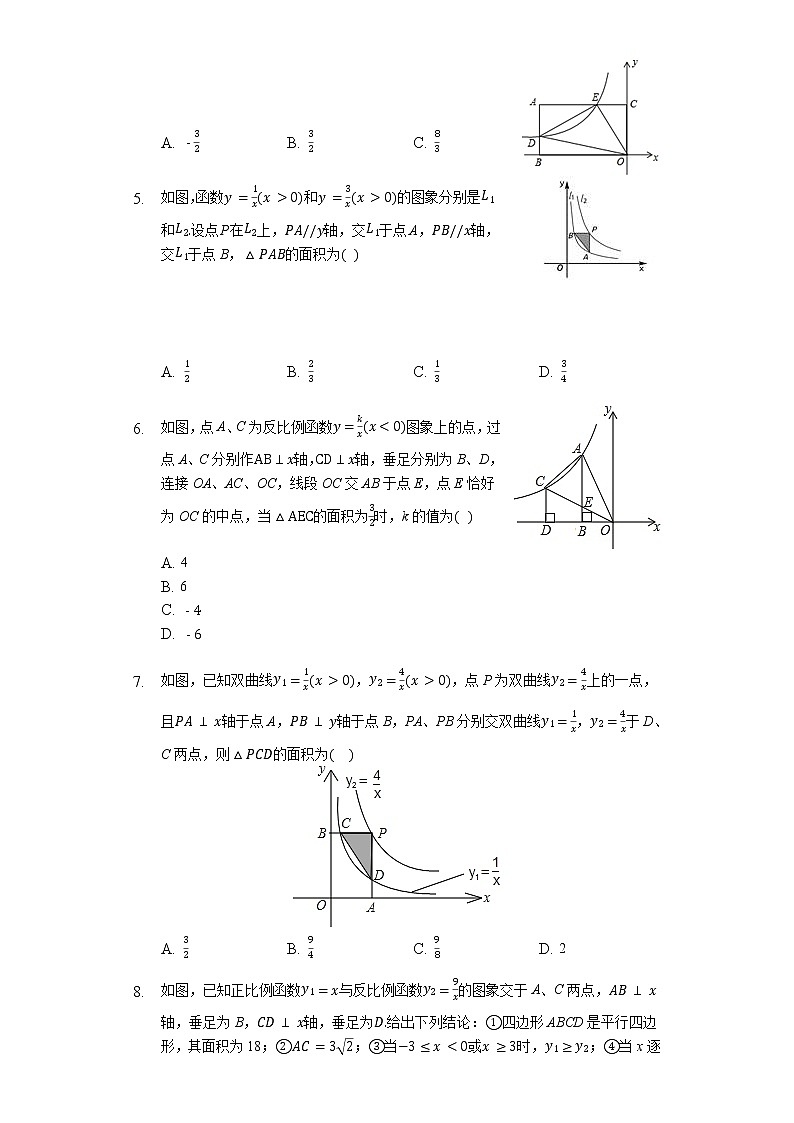
5. 如图，函数和的图象分别是和设点P在上，轴，交于点A，轴，交于点B，的面积为  
   
   
    

A.   B.  C.  D.

6. 如图，点A、C为反比例函数图象上的点，过点A、C分别作轴，轴，垂足分别为B、D，连接OA、AC、OC，线段OC交AB于点E，点E恰好为OC的中点，当的面积为时，k的值为

A. 4
B. 6
C.
D.

7. 如图，已知双曲线，，点P为双曲线上的一点，且轴于点A，轴于点B，PA、PB分别交双曲线，于D、C两点，则的面积为

A.  B.  C.  D. 2

8. 如图，已知正比例函数与反比例函数的图象交于A、C两点，轴，垂足为B，轴，垂足为给出下列结论：四边形ABCD是平行四边形，其面积为18；；当或时，；当x逐渐增大时，随x的增大而增大，随x的增大而减小．其中，正确结论的个数是         ．

A. 4个 B. 3个 C. 2个 D. 1个

二、填空题

9. 如图，正比例函数与反比例函数的图象有一个交点，轴于点平移直线，使其经过点B，得到直线l，则直线l的函数关系式是________．

10. 如图，点是反比例函数的图象上一点，点B是反比例函数上一点，AB与x轴平行，且的面积为5，则 ______ ．
     

11. 如图，一次函数ykxk与反比例函数的图像有公共点A直线lx轴于点N，与一次函数和反比例函数的图像分别交于点B、C则ABC的面积为        ．

12. 如图，A，B两点在反比例函数的图象上，C，D两点在反比例函数的图象上，轴于点E，轴于点F，，，，则的值是______．
    
    
    
    
    
    
     
13. 如图，正方形ABCD的顶点B在x轴上，点A、点C在双曲线上，若直线BC的解析式为，则k的值为___。

14. 如图，四边形ABCD为菱形，点A在y轴正半轴上，轴，点B，C在反比例函数上，点D在反比例函数上，那么点D的坐标为________。
     

15. 如图，在反比例函数的图象上有点，，，，它们的横坐标依次为1，2，3，，分别过这些点作x轴的垂线，垂足依次为，，，，分别以，，为对角线作平行四边形，另两顶点分别落在与上2，3，，为y轴，所构成的阴影部分的面积从左到右依次为，，，，记，，，，则____；____．

三、解答题

16. 如图，直线与反比例函数的图象交于点，点是反比例函数图象上一点，且．
    求k的值和点B坐标；
    若点P在x轴上，使得的面积为2，直接写出点P坐标．
    
    
    
    
    
    
     
17. 如图，矩形ABCD的顶点A、B分别在x轴、y轴上，，直线AB的解析式为，双曲线经过点D，与BC边相交于点E。
    
    填空：________；

连接AE、DE，试求的面积；

在x轴上有两点P、Q，其中点P可以使的值最小，而点Q可以使的值最大，请直接写出P、Q两点的坐标以及线段PQ的长。






 

18. 某种商品上市之初采用了大量的广告宣传，其销售量与上市的天数之间成正比，当广告停止后，销售量与上市的天数之间成反比如图，现已知上市30天时，当日销售量为120万件．
    写出该商品上市以后销售量万件与时间天数之间的表达式；
     求上市至第100天含第100天，日销售量在36万件以下不含36万件的天数；
    广告合同约定，当销售量不低于100万件，并且持续天数不少于12天时，广告设计师就可以拿到“特殊贡献奖”，那么本次广告策划，设计师能否拿到“特殊贡献奖”？说明：天数可以为小数，如天等

19. 如图，一次函数与反比例函数的图象交于，两点．

求反比例函数及一次函数的解析式；

在y轴上找一点P，使的值最小，

试确定点P的位置，并求满足条件的点P的坐标    

求的面积．






 

20. 如图，是药品研究所所测得的某种新药在成人用药后，血液中的药物浓度微克毫升用药后的时间小时变化的图象图象由线段OA与部分双曲线AB组成并测得当时，该药物才具有疗效．若成人用药4小时，药物开始产生疗效，且用药后9小时，药物仍具有疗效，则成人用药后，血液中药物需要多长时间达到最大浓度？

21. 如图，已知一次函数与反比例函数的图象相交于点，与x轴相交于点B．

求n与k的值；

以AB为边作菱形ABCD，使点C在x轴正半轴上，点D在第一象限，求点D的坐标；

观察反比函数的图象，当时，请直接写出自变量x的取值范围。






 

22. 在平面直角坐标系xOy中，对于点和，给出如下定义：如果，那么称点Q为点P的“关联点”例如：点的“关联点”为点，点的“关联点”为点．
     

点的“关联点”为_________，点的“关联点”为________；

如果点是反比例函数图象上点M的“关联点”，求点的坐标；

如果点是一次函数图象上点N的“关联点”，求点N的坐标．






 

23. 如图，一次函数与反比例函数的图象交于点和与y轴交于点C，与x轴交于点D．

求a、k的值；

过点A作轴于点E，若P为反比例函数图象的位于第一象限部分上的一点，且直线OP分所得的两部分面积之比为请求出所有符合条件的点P的坐标；

在的条件下，请在x轴上找一点Q，使得的周长最小，并求出点Q的坐标．

答案和解析

1. D
    

 
解：，
当时，；
当时，，
即无法判断，的大小．

2. A
 

 
解：设B的纵坐标为m，
轴，
的纵坐标也是m，
，
．

3. C
 

 
4. A
 

 
解：设点E的坐标为，
，
，
，，
，，，，，
的面积矩形OCAB的面积的面积的面积的面积，
，
，


5. B
 

 
解：设点，
是反比例函数图象上的点，
，

点，
轴，
点的纵坐标为，将点B的纵坐标代入反比例函数的解析式
得：，
，
同理可得：，
，，

6. C
 

 
解：设点C的坐标为，
点E恰好为OC的中点，
，即：，
，
，，
，
．

7. C
 

 解：作于E，于F，
双曲线，，且轴于点A，轴于点B，PA、PB分别依次交双曲线于D、C两点，
矩形BCEO的面积为：，
，，
，
，，
，
，
，
的面积为：．

8. C
 

 解：正比例函数与反比例函数的图象交于A、C两点，轴，垂足为B，轴，垂足为D，

可得，，，，

四边形ABCD是平行四边形，其面积为，正确；

，，错误；

根据图像，可得当或时，；正确；错误；

 
9.
 

 
解：正比例函数与反比例函数的图象有一个交点，
，
解得：，
故A，则，
解得：，
故正比例函数解析式为：，
轴于点B，平移直线，使其经过点B，
，
设平移后的解析式为：，
则，解得：，
故直线l对应的函数表达式是：．

10.
 

 
解：点是反比例函数的图象上一点，
，
点B是反比例函数上一点，AB与x轴平行，且的面积为5，
，
，
，
，
．

11.
 

 解：将代入一次函数解析式得：，即，
一次函数解析式为；
将代入反比例解析式得：，
反比例解析式为

，

点B横坐标为3，
将代入一次函数得：，将代入反比例解析式得：，

即，，A到BC的距离为：2，

则．

 
12. 2
 

 
解：连接OA、OC、OD、OB，
如图：
由反比例函数的性质可知，，
，
，
，
，
由两式解得，
则．

13. 6
 

 
解：分别过A，C作轴，轴，垂足分别为E，F，
，
在正方形ABCD中，，，
，
，
≌，
，，
直线BC的解析式为，
当时，，
解得，
点坐标，
设，则，
，C两点均在双曲线上，C点在直线上，

解得，
即，
故答案为6．

14.
 

 
解：设菱形的边长为a，，则，
四边形ABCD是菱形，
，
轴，
轴，
，
点D在反比例函数上，
，
，
，
过C作于E，


，
，
，
，
，
点B在反比例函数上，
，
，
，
，
，

15. 2，
 

 
解：反比例函数的图象上有点，，，，它们的横坐标依次为1，2，3，，
，，，，，
，，，，
，，．

16. 解：点在直线上，
，．
在反比例函数上，
，
．
点是反比例函数图象上，
，
解得，负值已舍去
；

如图，延长AB交x轴于点C，
设直线AB的解析式为，
则有，
解得，
直线AB的解析式为．
点C是直线与x轴的交点，
点C的坐标为，
设点P的坐标为，则，
依据可得，
，即，
解得或7，
点P的坐标为或．
 

 
17. 解：；
由知，，，
根据勾股定理得，，
，
；
作D关于x轴的对称点，直线与x轴的交点为所求P点，

由知，，，
点A到D是向右移动个单位，再向上移动4，
点B到点C是向右移动8个单位，再向上移动4，
，
，
点是点D关于x轴对称，
点，
设直线的解析式为，


直线的解析式为，
当时，，
．
作直线CD与x轴交于Q点，Q点即为所求Q点，
设直线CD的解析式为，过，，

解得：
，
当时，，
，
．
 

 
解：如图，

直线AB的解析式为，
令，则，
，
，令，则，
，
，
，
四边形ABCD是矩形，
，
，
，
，
过点D作轴于G，
，
，，
，
，
点D在反比例函数的图象上，
，

18. 解：当时，设，把代入得，；
当时，设，把代入得，
；
当时，由，
解得：，
即；
当时，由，
解得：，
不合条件，
共有8天；

当时，又得，，即，有6天；
当时，由，解得：，即，有6天，
共有天，因此设计师可以拿到特殊贡献奖．
 

 
19. 解：把代入，得，
反比例函数的解析式为；
把代入，得，
，
把、代入，得，
解得，
一次函数的解析式为；
作A的对称点，连接，交y轴于P，此时最小，
，
，
设直线的解析式为，
，
解得，
直线的解析式为，
令，得，
点P的坐标为；
过点B作轴于D，

由图知，，点，
，
，
，，



．

20. 解：设直线OA的解析式为，
把代入，得，解得，
即直线OA的解析式为
根据题意，在反比例函数的图象上，
则反比例函数的解析式为．
当时，解得负值舍去，
故成人用药后，血液中药物则至少需要6小时达到最大浓度．
 

 
21. 解：把点代入一次函数，可得； 
把点代入反比例函数，可得， 
解得 
一次函数与x轴相交于点B， 
， 
解得， 
点B的坐标为， 
如图，过点A作轴，垂足为E， 
过点D作轴，垂足为F， 
，， 
，，， 
， 
在中， 
， 
四边形ABCD是菱形， 
，， 
， 
轴，轴， 
， 
在与中， 
， 
≌， 
，， 
， 
点D的坐标为 
当时，，解得 
故当时，自变量x的取值范围是或
 

 
22. 解：由题意知如果，那么称点Q为点P的“关联点”，所以点的“关联点”为，点的“关联点”为；
将代入反比例函数，解得，再根据关联点的定义，知，故的坐标；   
同理根据关联点的定义，将代入一次函数，解得，
所以点N的坐标为．

23. 解：将代入反比例函数解析式得：，

解得：，

将代入一次函数解析式得：，解得：；
分两种情况考虑：
设P点存在，连接OP交AE于点F，

将代入反比例解析式得：，令一次函数中，，解得：，
则，，，
则，
又：：7，
，
又，，
，
，
设直线OF的方程为，将代入得：，
将直线OF方程与反比例函数解析式联立得：，
解得：或．
点在第一象限内，
；
设P点存在，连接OP交AC于点F，过F作轴，

：：7，
，
代入得：，
，在第二象限，
与图形矛盾，故此时P点不存在，
综上，P的坐标为；
点P存在时，，则P点关于x轴的对称点为，
连接交x轴于点Q，

设的方程为，将C与坐标代入得：，
解得：．
的方程为，
令，解得：，
则．