






数学必修41.2 任意的三角函数课文配套课件ppt
展开1.掌握正弦、余弦、正切函数的定义域.2.了解三角函数线的意义,能用三角函数线表示一个角的正弦、余弦和正切.3.能利用三角函数线解决一些简单的三角函数问题.
1.三角函数的定义域正弦函数y=sin x的定义域是R;余弦函数y=cs x的定义域是R;正切函数y=tan x的定义域是 .
2.三角函数线如图,设单位圆与x轴的正半轴交于点A,与角α的终边交于P点.过点P作x轴的垂线PM,垂足为M,过A作单位圆的切线交OP的延长线(或反向延长线)于T点.单位圆中的有向线段 、 、 分别叫做角α的正弦线、余弦线、正切线.记作:sin α= ,cs α= ,tan α= .
角是一个图形概念,也是一个数量概念(弧度数).作为角的函数——三角函数是一个数量概念(比值),但它是否也是一个图形概念呢?换句话说,前面我们学习了任意角的三角函数,主要从数上研究了它们,能否用几何方式来表示三角函数呢?这一节我们就来一起研究这个问题.
探究点一 三角函数线的概念及其作法
思考2 若角α为第三象限角,其终边与单位圆的交点为P(x,y),则sin α=y,cs α=x都是负数,此时角α的正弦值和余弦值分别用哪条线段表示?如何给线段MP、OM规定一个适当的方向,使它们的取值与点P的坐标一致?
答 过角α的终边与单位圆的交点P,过点P向x轴作垂线,垂足为M,则,-|MP|=y=sin α,-|OM|=x=cs α.
我们知道,直角坐标系内点的坐标与坐标轴的方向有关.设想将线段的两个端点规定一个为始点,另一个为终点,使得线段具有方向性,带有正负值符号.规定:线段从始点到终点与坐标轴同向时为正方向,反向时为负方向. 即规定当线段OM与x轴同向时,OM的方向为正向,且有正值x;当线段OM与x轴反向时,OM的方向为负向,且有负值x;其中x为P点的横坐标.这样,无论哪种情况
都有OM=x=cs α.同理,当角α的终边不在x轴上时,以M为始点、P为终点,规定:当线段MP与y轴同向时,MP的方向为正向,且有正值y;当线段MP与y轴反向时,MP的方向为负向,且有负值y;其中y为P点的纵坐标.这样,无论哪种情况都有MP=y=sin α.
小结 我们把这三条与单位圆有关的有向线段MP、OM、AT,分别叫做角α的正弦线、余弦线、正切线,统称为三角函数线.
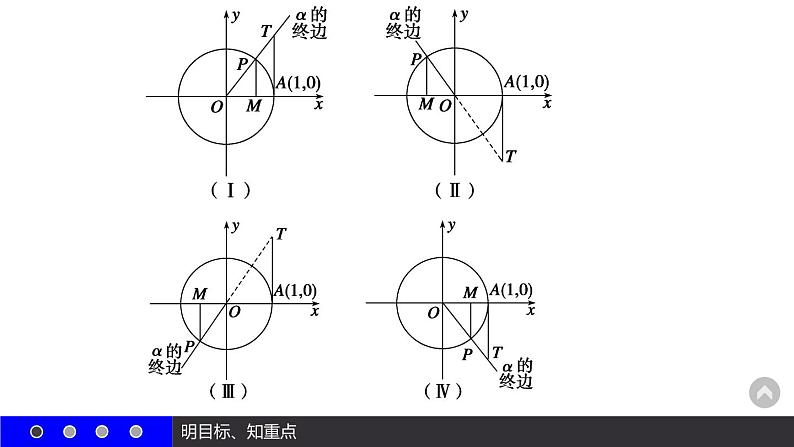
思考3 当角α的终边在第二、第三、第四象限时,你能分别作出它们的正弦线、余弦线和正切线吗?答 如下图:
探究点二 三角函数线的应用
导引 三角函数线是三角函数的几何表示,是任意角的三角函数定义的一种“形”的补充,线段的长度表示了三角函数绝对值的大小,线段的方向表示了三角函数值的正负.思考1 若α为任意角,则sin α,cs α的取值范围是多少?答 根据单位圆中正弦线和余弦线的变化规律可得-1≤sin α≤1,-1≤cs α≤1.
思考2 设α为锐角,你能根据正弦线和余弦线说明sin α+cs α>1吗?答 设角α的终边与单位圆交于点P,过P作PM⊥x轴,垂足为M,则sin α=MP,cs α=OM,OP=1.在Rt△OMP中,由两边之和大于第三边得MP+OM>OP,即sin α+cs α>1.
思考3 若α为任意角,根据单位圆中正弦线和余弦线的变化规律探究sin2α+cs2α与1的关系?答 当α的终边落在x轴上时,sin α=0,|cs α|=1,sin2α+cs2α=1;当α的终边落在y轴上时,|sin α|=1,cs α=0,sin2α+cs2α=1;当α的终边不落在坐标轴上时,sin α=MP,cs α=OM.在Rt△OMP中,|MP|2+|OM|2=|OP|2=1.∴sin2α+cs2α=1.综上所述,对于任意角α,都有sin2α+cs2α=1.
反思与感悟 作已知角的正弦线、余弦线、正切线时,要确定已知角的终边,再画线,同时要分清所画线的方向,对于以后研究三角函数很有用处.
解析 分别在单位圆中作出它们的三角函数线,由图可知:
例2 在单位圆中画出适合下列条件的角α的终边的范围,并由此写出角α的集合:
① ②
反思与感悟 利用单位圆中三角函数线,可以非常直观方便地求出形如sin x≥m或sin x≤m的三角函数的角的范围,起到“以形助数”的作用.
跟踪训练2 已知点P(sin α-cs α,tan α)在第一象限,在[0,2π)内,求α的取值范围.
探究点三 利用三角函数线求函数的定义域
思考 任意角的三角函数是在坐标系中定义的,角的范围是使函数有意义的实数集.根据任意角三角函数的定义可知正弦函数y=sin x的定义域是 ;余弦函数y=cs x的定义域是 ;正切函数y=tan x的定义域是 .在此基础上,可以求一些简单的三角函数的定义域.例如:
{x|x∈R,且x≠kπ
{x|2kπ≤x≤2kπ+π,k∈Z}
解 由题意,得自变量x应满足不等式组
则不等式组的解的集合如图(阴影部分)所示,
反思与感悟 求三角函数定义域时,一般应转化为求不等式(组)的解的问题.利用数轴或三角函数线是解三角不等式常用的方法.解多个三角不等式时,先在单位圆中作出使每个不等式成立的角的范围,再取公共部分.
1.角α(0<α<2π)的正、余弦线的长度相等,且正、余弦符号相异,那么α的值为( )
2.如图在单位圆中角α的正弦线、正切线完全正确的是( )
A.正弦线PM,正切线A′T′B.正弦线MP,正切线A′T′C.正弦线MP,正切线ATD.正弦线PM,正切线AT
4.利用三角函数线比较下列各组数的大小(用“>”或“<”连接):
答案 (1)> (2)> (3)<
1.三角函数线的意义三角函数线是用单位圆中某些特定的有向线段的长度和方向表示三角函数的值,三角函数线的长度等于三角函数值的绝对值,方向表示三角函数值的正负.具体地说,正弦线、正切线的方向同纵坐标轴一致,向上为正,向下为负;余弦线的方向同横坐标轴一致,向右为正,向左为负.三角函数线将抽象的数用几何图形表示出来,使得问题更形象直观,为从几何途径解决问题提供了方便.
2.三角函数线的画法定义中不仅定义了什么是正弦线、余弦线、正切线,同时也给出了角α的三角函数线的画法即先找到P、M、T点,再画出MP、OM、AT.注意三角函数线是有向线段,要分清始点和终点,字母的书写顺序不能颠倒.
高中数学人教版新课标A必修41.2 任意的三角函数课文内容课件ppt: 这是一份高中数学人教版新课标A必修41.2 任意的三角函数课文内容课件ppt,文件包含121第2课时ppt、121第2课时doc等2份课件配套教学资源,其中PPT共38页, 欢迎下载使用。
数学必修41.2 任意的三角函数教课内容ppt课件: 这是一份数学必修41.2 任意的三角函数教课内容ppt课件,文件包含121第1课时ppt、121第1课时doc等2份课件配套教学资源,其中PPT共49页, 欢迎下载使用。
高中数学人教版新课标A必修4第一章 三角函数1.2 任意的三角函数课文配套课件ppt: 这是一份高中数学人教版新课标A必修4第一章 三角函数1.2 任意的三角函数课文配套课件ppt













