






数学七年级下册第六章 实数6.2 立方根背景图ppt课件
展开2.我们把求平方根的运算称之为
开平方运算与乘方运算是
一般地,如果一个数的平方等于a,那么这个数叫做a的平方根,记作:
1.已知正方形的面积为81,求边长
2.已知一个正方体的体积是27,求棱长
解:设边长为x,则由题意得: x2=81 x=±9 因为x>0,所以x=9
解:设棱长为x,则由题意得:x3=27 x=3
思考:这两题求解过程有什么区别和联系?
相同点:都是知道一个数乘方的结果,求这个数;不同点:1.题是平方,2.题是立方
你能类比平方根定义,给立方根下定义吗?
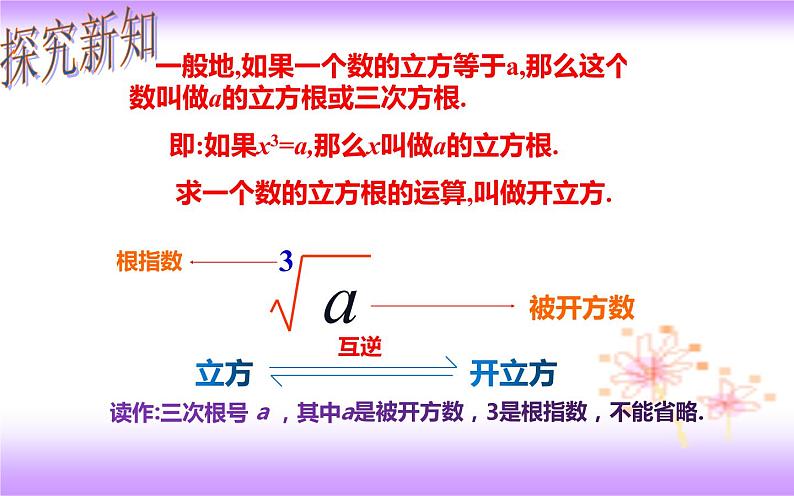
一般地,如果一个数的立方等于a,那么这个数叫做a的立方根或三次方根. 即:如果x3=a,那么x叫做a的立方根. 求一个数的立方根的运算,叫做开立方.
读作:三次根号 a ,其中a是被开方数,3是根指数,不能省略.
(1)27. (2)-27. (3) (4)-0.064. (5)0.
∴-27的立方根是-3
∴-0.064的立方根是-0.4
思考:正数、0、负数的立方根各有什么特点?
正数的立方根是正数,负数的立方根是负数,0的立方根是0.
因为 =____, =_____;所以 _____ 因为 =____, =_____;所以 _____
比较两式子计算结果,你能得出什么样的结论
求一个负数的立方根,可以先求出这个负数绝对值的立方根,然后再取它的相反数。利用立方根的性质进行化简。
你能归纳出平方根和立方根的异同点吗?
1.被开方数的小数点向右或向左移动3位,则它的立方根的小数点相应地向相同方向移动1位;
2.正数的立方根中,被开方数越大,则对应的立方根也越大.
应用: 1. 体积分别为27, 64, 50的正方体的棱长分别是多少?试比较它们的大小.
解:棱长分别是 , , ; ∵27﹤50﹤64, ∴ , 即 .
2. 根据下表回答下列问题:
1.判断下列说法是否正确,并说明理由
(2) 25的平方根是5
(3) -64没有立方根
(5) 0的平方根和立方根都是0
(1).-8的立方根是( )A. 2 B. -2 C. D.
(1)1的平方根是____;立方根为____;算术平方根为_____. (2)平方根是它本身的数是____.(3)立方根是其本身的数是____.(4)算术平方根是其本身的数是____.
(5) 的平方根为 .
4.分别求下列各式的值: (1)
5. 已知一个如图构造形状的正方体魔方的体积为216 cm3,试求构成它每个小正方体的棱长。
解:由题意,该魔方一共有33=27个小正方体组成,设小正方体的棱长为x cm,则有:27x3=216,得x3=8,即x=2. 所以小正方体的棱长为2 cm.
相同点:①0的平方根、立方根都有一个是0; ②平方根、立方根都是开方的结果。不同点:①定义不同; ②个数不同; ③表示方法不同; ④被开方数的取值范围不同。
1.立方根的定义,性质,计算。
2.立方根与平方根的异同。
教科书52页,习题 6.2 3,5题
人教版七年级下册6.2 立方根说课ppt课件: 这是一份人教版七年级下册6.2 立方根说课ppt课件,共14页。PPT课件主要包含了没有平方根,你还记得吗,立方根的定义,开立方,立方根的性质,想一想,1立方根的特征,练一练,引伸探究2,探究3等内容,欢迎下载使用。
初中数学第六章 实数6.2 立方根精品ppt课件: 这是一份初中数学第六章 实数6.2 立方根精品ppt课件,共25页。PPT课件主要包含了学习目标,x327,立方根的概念,立方根的表示,根指数,被开方数,读作三次根号a,立方根的性质,零的立方根是零,知识要点等内容,欢迎下载使用。
初中数学人教版七年级下册6.2 立方根授课ppt课件: 这是一份初中数学人教版七年级下册6.2 立方根授课ppt课件,共22页。PPT课件主要包含了三次根号,根指数index,不能省略,读作三次根号a,开立方的概念,两个互为相反数,一个为正数,没有平方根,一个为负数,可以为任何数等内容,欢迎下载使用。













