2021学年5.1.1 相交线教学ppt课件

这是一份2021学年5.1.1 相交线教学ppt课件，共22页。PPT课件主要包含了课堂讲解，课时流程，北京立交桥，相交线，平行线，知识点，邻补角的定义及性质，有一条公共边，邻补角，对顶角的定义及性质等内容，欢迎下载使用。
邻补角的定义及性质对顶角的定义及性质
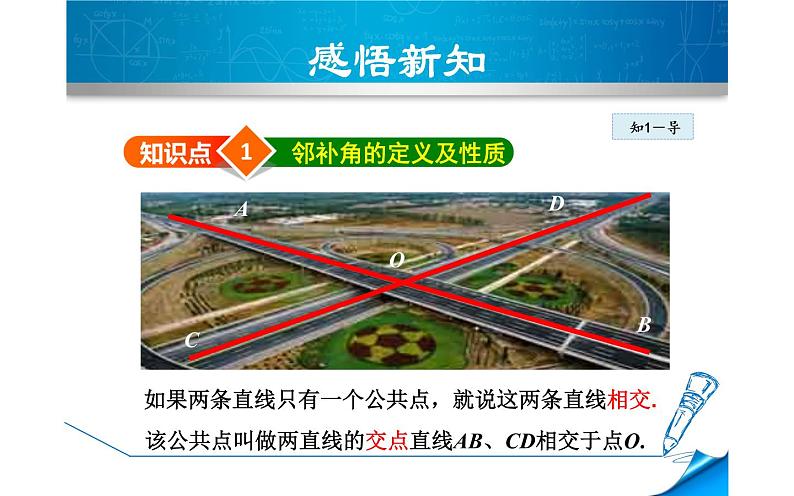
如果两条直线只有一个公共点，就说这两条直线相交.
该公共点叫做两直线的交点直线AB、CD相交于点O.
∠1和∠2也是直线AB、CD相交得到的，它们不仅有一个公共顶点O，还有一条公共边OC，
像这样的两个角叫做邻补角 .
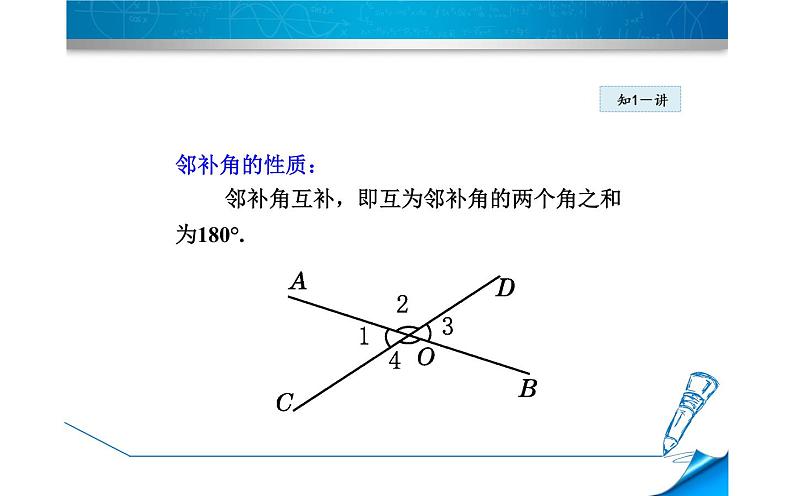
∠2与∠3，∠3与∠4，∠1与∠4都是邻补角.
2.角的另一边互为反向延长线.
邻补角的性质： 邻补角互补，即互为邻补角的两个角之和为180°.
如图所示，直线AB，CD，EF相交于点O，指出∠AOC，∠EOB的邻补角．
找一个角的邻补角时，可先固定一边，反向延长另一边，则由固定的一边和另一边的反向延长线组成的角即是原角的邻补角．∠AOC的邻补角有两个：固定射线OA，反向延长射线OC得到∠AOD；固定射线OC，反向延长射线OA得到∠BOC，它们都是∠AOC的邻补角．同理，∠EOB的邻补角也有两个，为∠BOF和∠AOE.∠AOC的邻补角是∠AOD，∠BOC；∠EOB的邻补角是∠BOF和∠AOE.
判断两个角是不是邻补角，应从两个方面去看：一看这两个角有没有公共边；二看这两个角的另一边是否互为反向延长线．
2 下列选项中，∠1与∠2互为邻补角的是(　　)
3 如图，∠1的邻补角是(　　) A．∠BOC B．∠BOE和∠AOF C．∠AOF D．∠BOC和∠AOF
4 【中考·柳州】如图，∠α的度数等于(　　) A．135° B．125° C．115° D．105°
有一个公共顶点一个角的两边是另一个角的两边的反向延长线，那么这两个角互为对顶角.
2.角的两边互为反向延长线.
∠1=∠3 （或 ∠2=∠4）
解：直线AB与CD相交于O点
由邻补角的定义，可得∠1+∠2=180° ∠2+∠3=180
同样的道理 ∠2=∠4
如图，∠1与∠2是对顶角的是(　 　)
判断两个角是不是对顶角，要紧扣对顶角的定义，A图中∠1和∠2的顶点不同；B图中∠1和∠2的两边都不是互为反向延长线；C图中的∠1和∠2符合定义；D图中∠1和∠2有一条公共边．
判断两个角是否互为对顶角的方法：一看它们有没有公共顶点；二看这两个角的两边是否互为反向延长线，实质就是看这两个角是否是两条直线相交所成的没有公共边的两个角．
如图，小强和小丽一起玩跷跷板，横板AB绕O 上下转动，当小强从A到A′的位置时， ∠AOA′＝45°，则∠BOB′的度数为________， 理由是__________________.
如图，直线a, b相交，∠1 = 40°， 求∠2, ∠3, ∠4的度数.由邻补角的定义，得∠2 = 180°-∠1 = 180°-40°=140°；由对顶角相等，得∠3= ∠1=40° ， ∠4= ∠2 = 140°.
变式1：如图，直线a, b相交，若∠2是∠1的3倍，求∠3的度数？
变式2：如图，直线a, b相交，若∠2-∠1=40°， 求∠4的度数？