




人教版七年级下册第六章 实数6.3 实数复习课件ppt
展开1.掌握平方根和立方根的概念,并能求出某些数的平方根和立方根.2.掌握实数的概念和意义,理解实数的分类,并能运用运算律进行实数的相关运算.
1.经历数系扩充、探求实数性质及其运算规律、借助计算器探索数学规律等活动过程.2.了解无理数和实数的概念,知道实数与数轴上的点一一对应,能求实数相反数与绝对值.
1.发展抽象概括能力,并在活动中进一步发展学生独立思考、合作交流的能力.2.能运用实数的运算解决简单的实际问题,提高应用意识,发展解决问题的能力,从中体会数学的应用价值.
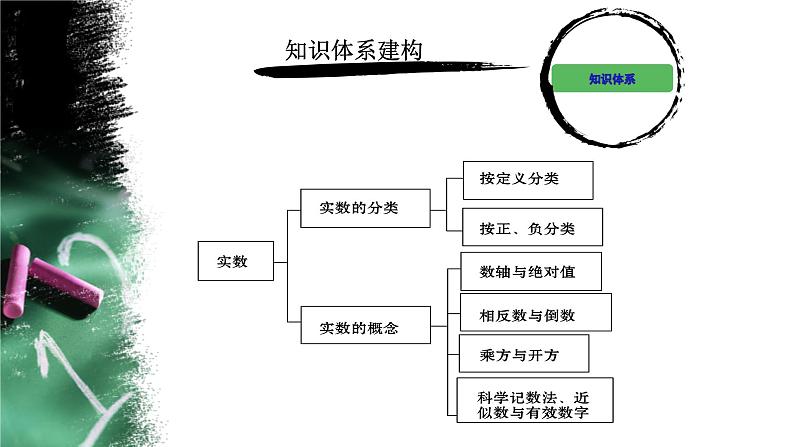
2. 按正负分类
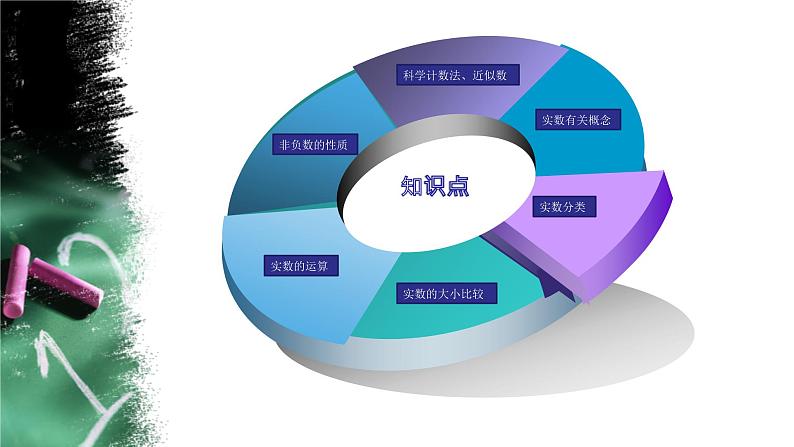
1.数轴(1) 数轴的三要素:原点、正方向、单位长度; (2)实数与数轴上的点是一一对应的. 2.相反数(1)实数a的相反数是-a,0的相反数是0;(2)a与b互为相反数⇔a+b=0. 3.倒数(1)实数a的倒数是 (a≠0),0没有倒数; (2)a与b互为倒数⇔ab=1.4.绝对值(1)数轴上表示数a的点与原点的距离,叫做数a的绝对值,记作|a|.
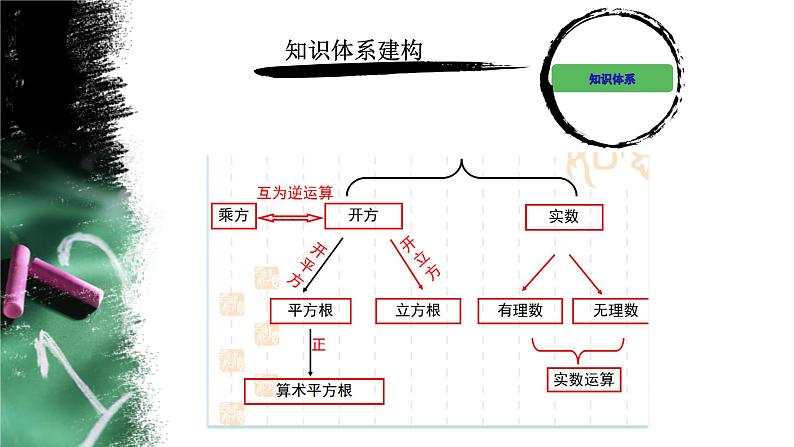
5.平方根、算术平方根、立方根1. (一)平方根 (1) 定义:如果一个数x的平方等于a,即x2=a,那么这个数x就叫 做a的平方根(也叫二次方根),数a的平方根记作___________.(2)一个正数有两个平方根,它们互为相反数;0只有一个平方根, 它是0本身;负数没有平方根.(二)算术平方根
(三)立方根(1)定义:如果一个数x的立方等于a,即x3=a,那么这个数x叫做a的立方根(也叫三次方根),数a的立方根记作 .(2)一个正数有一个正的立方根,一个负数有一个负的立方根,0的立方根是0.
1.科学记数法把一个数N表示成 a×10n(1≤|a|<10,n是整数)的形式叫科学记数法.当|N|>10时,n等于原数N的整数位数减1;当0<|N|<1时,n是一个负整数,它的绝对值等于原数中左起第一个非零数字前零的个数(含整数位上的零).2.近似数与精确度一个近似数,四舍五入到哪一位,就说这个近似数精确到哪一位,这时,用精确度来表示。例如:0.674 5精确到百分位为0.67,精确到千分位为0.675.
1.基本运算 加法、减法、乘法、除法、乘方、开方. 2.基本法则 加法法则、减法法则、乘法法则、除法法则、乘方法则. 3.运算律 加法交换律、加法结合律、乘法交换律、乘法结合律、 乘法分配律.4.运算顺序(1)先算乘方、开方,再算乘除,最后算加减;(2)同级运算,按照从左至右的顺序进行;(3)如果有括号,就先算小括号里的,再算中括号里的,最后算大括号里的,计算时,可以结合运算律,使问题简单化.
1.在数轴上表示两个数的点,右边的点表示的数总比左边的点表示的数大.2.正数大于零,负数小于零,正数大于一切负数;两个负数比较大小,绝对值大的数反而小.3.作差比较法(1)a-b>0⇔a>b;(2)a-b=0⇔a=b;(3)a-b<0⇔a
A.点A的左边 B.点A与点B之间C.点B与点C之间 D.点B与点C之间或点C的右边
解析 ∵|a|>|b|>|c|,∴点A到原点的距离最大,点B其次,点C最小,又∵AB=BC,∴原点O的位置是在点C的右边,或者在点B与点C之间,且靠近点C的地方.答案 D
数学人教版16.1 二次根式教学课件ppt: 这是一份数学人教版16.1 二次根式教学课件ppt,共15页。PPT课件主要包含了复习导入,复习目标,知识回顾,二次根式的性质,二次根式的运算,解原式13,巩固练习,应用拓展,二次根式,课堂小结等内容,欢迎下载使用。
初中数学人教版七年级下册6.3 实数教课课件ppt: 这是一份初中数学人教版七年级下册6.3 实数教课课件ppt,共19页。PPT课件主要包含了学习目标,有理数的加法,有理数的减法,有理数的乘法,有理数的除法,有理数的乘方,实数的运算顺序,实数的运算律,1加法交换律,2加法结合律等内容,欢迎下载使用。
数学七年级下册6.3 实数评课课件ppt: 这是一份数学七年级下册6.3 实数评课课件ppt,共19页。PPT课件主要包含了创设情境引入新课,合作交流解决问题,拓展延伸操作感知,反思小结,谈谈本节课你的收获,课后作业等内容,欢迎下载使用。













