






高中数学人教版新课标A选修1-12.3抛物线多媒体教学课件ppt
展开通过动画展示抛物线的形成,利用图片直观感知抛物线在我们日常生活中的存在,培养学生善于观察的良好品质,同时激发了学生探索新知的欲望,充分调动学生学习的积极性和主动性.运用类比的思想,类比椭圆的性质和双曲线的性质学习抛物线的性质. 例1是利用抛物线的几何性质求双曲线的标准方程;例2是求直线与抛物线相交的弦长问题,利用抛物线的定义和数形结合的方法帮助学生理解。利用动画展示抛物线的对称性.
类比椭圆、双曲线的几何性质,你认为可以讨论抛物线的哪些几何性质?
抛物线有许多重要性质.我们根据抛物线的标准方程
研究它的一些简单几何性质:
抛物线的简单几何性质
因为p>0,由方程(1)可知,对于抛物线(1)上的点M (x,y),x≥0,所以这条抛物线在y轴的右侧,开口方向与x轴正向相同; 当x的值增大时,|y|也增大,这说明抛物线向右上方和右下方无限延伸.
以-y代y,方程(1)不变,所以这条抛物线关于x轴对称. 我们把抛物线的对称轴叫做抛物线的轴.
抛物线和它的轴的交点叫做抛物线的顶点.在方程(1)中,当y=0时,x=0,因此抛物线(1)的顶点就是坐标原点.
抛物线上的点M与焦点的距离和它到准线的距离的比,叫做抛物线的离心率,用e表示.由抛物线的定义可知,e=1.
过焦点而垂直于对称轴的弦AB,称为抛物线的通径.
利用抛物线的顶点、通径的两个端点可较准确画出反映抛物线基本特征的草图.
2p越大,抛物线张口越大.
抛物线的其它几何性质
连接抛物线上任意一点与焦点的线段叫做抛物线的焦半径.
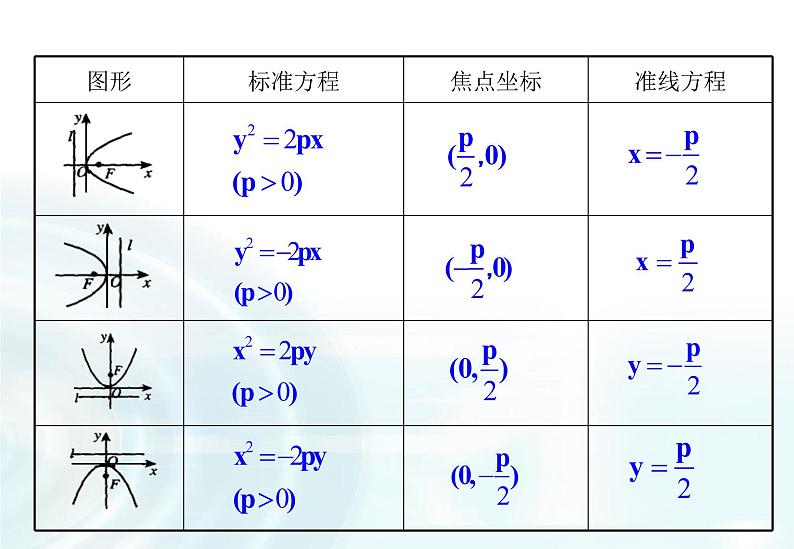
y2 = 2px(p>0)
y2 = -2px(p>0)
x2 = 2py(p>0)
x2 = -2py(p>0)
(1)抛物线只位于半个坐标平面内,虽然它也可以无限延伸,但没有渐近线;(2)抛物线只有一条对称轴,没有对称中心;(3)抛物线只有一个顶点,一个焦点,一条准线;(4)抛物线的离心率e是确定的,为1;(5)抛物线的通径为2p, 2p越大,抛物线的张口越大.
解:因为抛物线关于x轴对称,它的顶点在坐标原点,并且经过点M(2, ),所以,可设它的标准方程为
因为点M在抛物线上,所以
因此,所求抛物线的标准方程是
抛物线几何性质的应用
分析:由抛物线的方程可以得到它的焦点坐标,又直线l的斜率为1,所以可以求出直线l的方程;与抛物线的方程联立,可以求出A,B两点的坐标;利用两点间的距离公式可以求出∣AB|.这种方法虽然思路简单,但是需要复杂的代数运算.
下面,我们介绍另外一种方法——数形结合的方法.
还可以如何求x1+x2?
分析:运用抛物线的定义和平面几何知识来证比较简捷.
如上题,求证:以AB为直径的圆和抛物线的准线相切.
所以EH是以AB为直径的圆E的半径,且EH⊥l,因而圆E和准线l相切.
证明:如图,设AB的中点为E,过A,E,B分别向准线l引垂线AD,EH,BC,垂足分别为D,H,C,
则|AF|=|AD|,|BF|=|BC|
∴|AB|=|AF|+|BF| =|AD|+|BC| =2|EH|
2.抛物线 的弦AB垂直x轴,若|AB|= , 则焦点到AB的距离为 。
1.做一做(请把正确的答案写在横线上)(1)顶点在原点,对称轴为y轴且过(4,1)的抛物线方程是 .(2)已知点(-2,3)与抛物线y2=2px(p>0)的焦点的距离是5,则p= .(3)抛物线y=2px2(p>0)的对称轴为 .
抛物线只位于半个坐标平面内,虽然它也可以无限延伸,但没有渐近线;
抛物线只有一条对称轴,没有对称中心;
抛物线的离心率是确定的,等于1.
抛物线只有一个顶点,一个焦点,一条准线;
高中数学2.3.2抛物线的几何性质图文课件ppt: 这是一份高中数学2.3.2抛物线的几何性质图文课件ppt,共20页。PPT课件主要包含了抛物线的定义,复习与巩固,抛物线的几何性质,对称性,开口方向,离心率,例题讲解,变式训练1,当堂检测,y2-16x等内容,欢迎下载使用。
高中数学人教版新课标B选修1-12.3.2抛物线的几何性质教学演示ppt课件: 这是一份高中数学人教版新课标B选修1-12.3.2抛物线的几何性质教学演示ppt课件,共50页。PPT课件主要包含了有两个或一个,有且只有一个,抛物线的综合运用,点击右图进入等内容,欢迎下载使用。
2020-2021学年2.3.2抛物线的几何性质备课ppt课件: 这是一份2020-2021学年2.3.2抛物线的几何性质备课ppt课件,共40页。PPT课件主要包含了焦点弦问题,点击右图进入等内容,欢迎下载使用。













