2021年安徽省合肥三十八中分校中考数学一模试卷 解析版

这是一份2021年安徽省合肥三十八中分校中考数学一模试卷 解析版，共23页。试卷主要包含了选择题，填空题等内容，欢迎下载使用。
2021年安徽省合肥三十八中分校中考数学一模试卷
一、选择题（本大题共10小题，每小题4分，满分40分）
1．（4分）下面四个数中，比﹣1小的是（　　）
A．﹣2 B． C．﹣0.1 D．0
2．（4分）计算（﹣x）2•x3所得的结果是（　　）
A．x5 B．﹣x5 C．x6 D．﹣x6
3．（4分）2020年1～7月份安徽实现进出口392.5亿美元，将392.5亿用科学记数法表示为（　　）
A．3.925×108 B．3.925×109 C．3.925×1010 D．39.25×1010
4．（4分）如图，这个几何体是将一个正方体中间挖出一个圆柱体后的剩余部分，该几何体的左视图是（　　）

A． B． C． D．
5．（4分）下列计算正确的是（　　）
A． B． C． D．
6．（4分）为庆祝祖国70华诞，某校开展了“祖国在我心中”知识竞赛，并将所有参赛学生的成绩统计整理制成如下统计图，根据图中的信息判断：关于这次知识竞赛成绩的中位数的结论正确的是（　　）

A．中位数在60分～70分之间
B．中位数在70分～80分之间
C．中位数在80分～90分之间
D．中位数在90分～100分之间
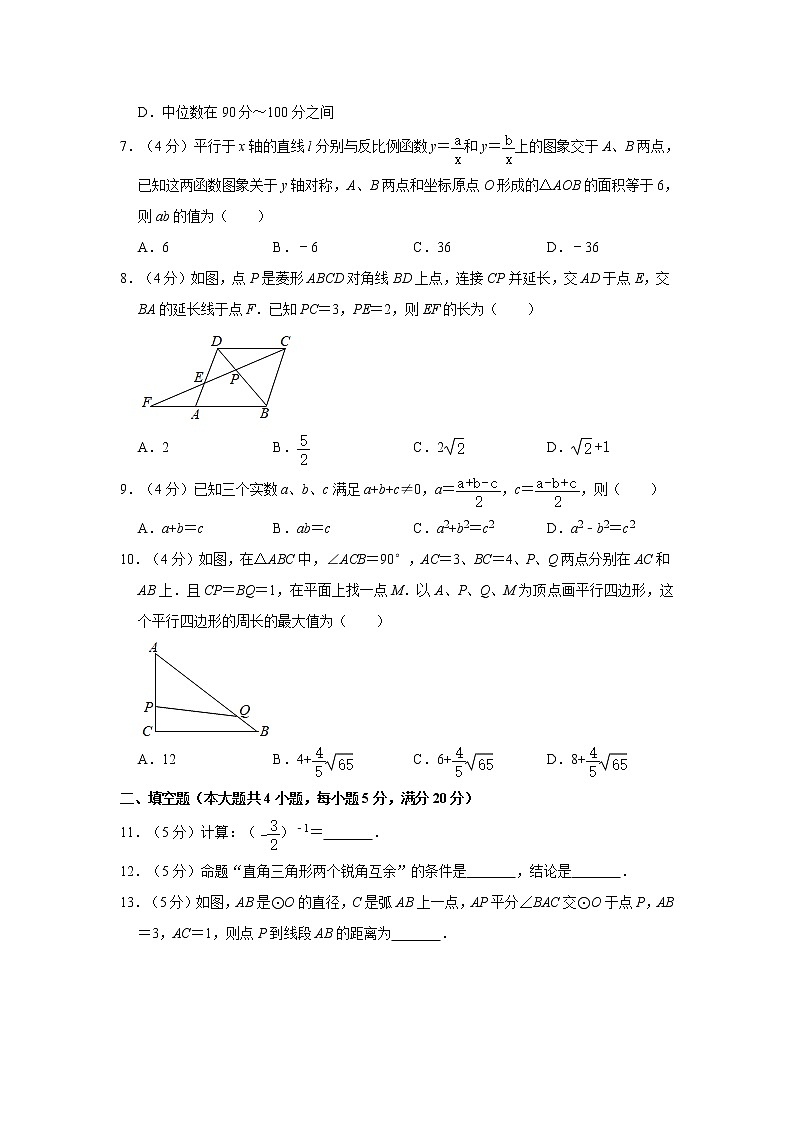
7．（4分）平行于x轴的直线l分别与反比例函数y＝和y＝上的图象交于A、B两点，已知这两函数图象关于y轴对称，A、B两点和坐标原点O形成的△AOB的面积等于6，则ab的值为（　　）
A．6 B．﹣6 C．36 D．﹣36
8．（4分）如图，点P是菱形ABCD对角线BD上点，连接CP并延长，交AD于点E，交BA的延长线于点F．已知PC＝3，PE＝2，则EF的长为（　　）

A．2 B． C．2 D．
9．（4分）已知三个实数a、b、c满足a+b+c≠0，a＝，c＝，则（　　）
A．a+b＝c B．ab＝c C．a2+b2＝c2 D．a2﹣b2＝c2
10．（4分）如图，在△ABC中，∠ACB＝90°，AC＝3、BC＝4、P、Q两点分别在AC和AB上．且CP＝BQ＝1，在平面上找一点M．以A、P、Q、M为顶点画平行四边形，这个平行四边形的周长的最大值为（　　）

A．12 B．4+ C．6+ D．8+
二、填空题（本大题共4小题，每小题5分，满分20分）
11．（5分）计算：（）﹣1＝　 　．
12．（5分）命题“直角三角形两个锐角互余”的条件是　 　，结论是　 　．
13．（5分）如图，AB是⊙O的直径，C是弧AB上一点，AP平分∠BAC交⊙O于点P，AB＝3，AC＝1，则点P到线段AB的距离为　 　．

14．（5分）在平面直角坐标系中，垂直于x轴的直线l分别与函数y＝﹣x2+4x+5的图象在x轴上方部分和函数y＝﹣x+3的图象交于A、B两点，与x轴交于点C，设点C的坐标为（m，0），若AB＝5BC，则m的值为　 　．
三、（本大题共2小题。每小题8分，满分16分）
15．（8分）解方程：．
16．（8分）如图，在边长为1个单位长度的小正方形组成的12×12网格中，给出了格点△ABC（顶点是网格线的交点），并建立平面直角坐标系．
（1）将线段AB绕旋转中心P（3，1）顺时针旋转90°，得到线段A1B1，请在网格内画出线段A1B1；
（2）以原点O为位似中心，将△ABC作位似变换且放大到原来的两倍，得到△A2B2C2，请在网格内画出△A2B2C2．

四、（本大题共2小题。每小题10分，满分20分）
17．（10分）某书店购进甲、乙两种畅销书共20包花费资金3.45万元，已知甲种书进价为每包0.2万元，其销售利润率为25%；乙种书进价为每包0.15万元，其销售利润率为20%．全部售完后，求该书店共获得的利润．（利润＝售价﹣成本，利润率＝（售价﹣成本）÷成本×100%）
18．（10分）观察以下等式：第1个等式：100﹣9×11＝1；第2个等式：400﹣18×22＝4；第3个等式：900﹣27×33＝9；第4个等式：1600﹣36×44＝16；第5个等式：2500﹣45×55＝25；按照以上规律，解决下列问题：
（1）写出第6个等式：　 　；
（2）写出你猜想的第n个等式：　 　（用含n用的等式表示），并证明．
五、（本大题共2小题。每小题10分，满分20分）
19．（10分）我国古代数学家刘徽将勾股形（古人称直角三角形为勾股形）分割成一个正方形和两对全等的直角三角形．如图，在△ABC中，∠C＝90°，四边形CDEF为正方形．△ADE≌△AGE，△BGE≌△BFE．已知AB＝10cm，∠BAC＝44°，求正方形CDEF的边长（结果保留位一位小数）．（参考数据：sin44°≈0.69，cos44°≈0.72°，tan44°≈0.97，sin22°≈0.37，cos22°≈0.93，tan22°≈0.40）

20．（10分）如图1，在△ABC中，∠C＝90°．
（1）用尺规作图作出斜边AB的中点D（保留作图痕迹，不写作法）；
（2）如图2，过A、C、D三点的⊙O与BC交于点E，若AC＝CE，求∠B的度数．

六、（本题满分12分）
21．（12分）九（1）班针对“你最向往的研学目标”的问题对全班学生进行了调查（共提供A、B、C、D四个研学目标，每名学生从中分别选一个目标），并根据调查结果列出统计表绘制扇形统计图．
男、女生最向往的研学目标人数统计表
目标
A
B
C
D
男生（人数）
7
m
2
5
女生（人数）
9
4
2
n
根据以上信息解决下列问题：
（1）m＝　 　，n＝　 　；
（2）扇形统计图中A所对应扇形的圆心角度数为　 　；
（3）从最向往的研学目标为C的4名学生中随机选取2名学生参加竞标演说，求所选取的2名学生中恰好有一名男生、一名女生的概率．

七、（本大题12分）
22．（12分）已知二次函数y＝﹣x2+bx+c和一次函数y＝mx+n的图象都经过点A（﹣3，0），且二次函数y＝﹣x2+bx+c的图象经过点B（0，3），一次函数y＝mx+n的图象经过点C（0，﹣1）．
（1）分别求m、n和b、c的值；
（2）点P是二次函数y＝﹣x2+bx+c的图象上一动点，且点P在x轴上方，写出△ACP的面积S关于点P的横坐标
x的函数表达式，并求S的最大值．
八、（本大题14分）
23．（14分）如图1，在矩形ABCD中，AD＝2AB，点P在AD边上，连接BP，过点D作BP的垂线交BP的延长线于点E，连接BD．
（1）连接AE，过点A作AF⊥AE交BE于点F．
①若，求sin∠DBE的值；
②求证：DE＝2BF．
（2）如图2，在BE的延长线上取一点G，连接DG，若∠GDE＝∠ADB，取BG的中点M，连接AM，求证：AM＝（BE﹣GE）．


2021年安徽省合肥三十八中分校中考数学一模试卷
参考答案与试题解析
一、选择题（本大题共10小题，每小题4分，满分40分）
1．（4分）下面四个数中，比﹣1小的是（　　）
A．﹣2 B． C．﹣0.1 D．0
【分析】有理数大小比较的法则：①正数都大于0；②负数都小于0；③正数大于一切负数；④两个负数，绝对值大的其值反而小，据此判断即可．
【解答】解：∵﹣2＜﹣1，＞﹣1，﹣0.1＞﹣1，0＞﹣1，
∴所给的四个数中，比﹣1小的是﹣2．
故选：A．
2．（4分）计算（﹣x）2•x3所得的结果是（　　）
A．x5 B．﹣x5 C．x6 D．﹣x6
【分析】积的乘方，等于把每个因式分别乘方，再把所得的幂相乘；同底数幂相乘，底数不变指数相加，计算后直接选取答案．
【解答】解：（﹣x）2x3＝x2•x3＝x5．
故选：A．
3．（4分）2020年1～7月份安徽实现进出口392.5亿美元，将392.5亿用科学记数法表示为（　　）
A．3.925×108 B．3.925×109 C．3.925×1010 D．39.25×1010
【分析】科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值≥10时，n是正数；当原数的绝对值＜1时，n是负数．
【解答】解：392.5亿＝392500000000＝3.925×1010．
故选：C．
4．（4分）如图，这个几何体是将一个正方体中间挖出一个圆柱体后的剩余部分，该几何体的左视图是（　　）

A． B． C． D．
【分析】左视图是从左边看得出的图形，结合所给图形及选项即可得出答案．
【解答】解：从左边看一个正方形被分成三部分，两条分线是虚线；
故选：D．
5．（4分）下列计算正确的是（　　）
A． B． C． D．
【分析】根据二次根式的运算法则即可求出答案．
【解答】解：A、，故A错误．
B、，故B正确．
C、，故C错误．
D、，故D错误．
故选：B．
6．（4分）为庆祝祖国70华诞，某校开展了“祖国在我心中”知识竞赛，并将所有参赛学生的成绩统计整理制成如下统计图，根据图中的信息判断：关于这次知识竞赛成绩的中位数的结论正确的是（　　）

A．中位数在60分～70分之间
B．中位数在70分～80分之间
C．中位数在80分～90分之间
D．中位数在90分～100分之间
【分析】求出调查总人数，再根据中位数的意义求解即可．
【解答】解：调查总人数为：30+90+90+60＝270（人），
将这270人的得分从小到大排列后，处在第135、136位的两个数都落在80～90分之间，
因此，中位数在80分～90分之间；
故选：C．
7．（4分）平行于x轴的直线l分别与反比例函数y＝和y＝上的图象交于A、B两点，已知这两函数图象关于y轴对称，A、B两点和坐标原点O形成的△AOB的面积等于6，则ab的值为（　　）
A．6 B．﹣6 C．36 D．﹣36
【分析】由题意可知a+b＝0，由反比例函数系数k的几何意义得到|a﹣b|＝6，即可求得a＝6，b＝﹣6，即可求得ab＝﹣36．
【解答】解：∵反比例函数y＝和y＝上的图象关于y轴对称，
∴a+b＝0；
∵S△AOB＝6，
∴|a﹣b|＝6；
∴a＝6，b＝﹣6，
∴ab＝﹣36
故选：D．
8．（4分）如图，点P是菱形ABCD对角线BD上点，连接CP并延长，交AD于点E，交BA的延长线于点F．已知PC＝3，PE＝2，则EF的长为（　　）

A．2 B． C．2 D．
【分析】根据菱形的性质得AD∥BC，然后由相似三角形的判定与性质得EF：（EF+EC）＝AE：BC＝1：3，最后求解即可得到答案．
【解答】解：∵四边形ABCD是菱形，
∴AD∥BC，
∴△DEP～△BCP，△AFE～△BFC，
∵PC＝3，PE＝2，
∴BC：DE＝PC：PE＝3：2，
设BC＝3a，则DE＝2a，
∴AE＝a，
∵△AFE～△BFC，
∴EF：（EF+EC）＝AE：BC＝1：3，
解得：EF＝
故选：B．
9．（4分）已知三个实数a、b、c满足a+b+c≠0，a＝，c＝，则（　　）
A．a+b＝c B．ab＝c C．a2+b2＝c2 D．a2﹣b2＝c2
【分析】将a，c相加可得c＝0，再将c代入，即可得a，b的关系．
【解答】解：∵，
∴c＝0，
∴，
∴a﹣b+c＝0，
∴a＝b，
∴a2﹣b2＝（a﹣b）（a+b）＝0＝c2．
故选：D．
10．（4分）如图，在△ABC中，∠ACB＝90°，AC＝3、BC＝4、P、Q两点分别在AC和AB上．且CP＝BQ＝1，在平面上找一点M．以A、P、Q、M为顶点画平行四边形，这个平行四边形的周长的最大值为（　　）

A．12 B．4+ C．6+ D．8+
【分析】先依据勾股定理以及相似三角形的性质，即可得到PQ的长，再分三种情况，即可得到以A、P、Q、M为顶点的平行四边形的周长，进而得出周长的最大值．
【解答】解：由勾股定定理得：AB＝5，则AQ＝4；
过点Q作QN⊥AC，垂足为N，则QN∥BC，
则AN：NC＝AQ：QB＝4，
则AN＝，
∴PN＝﹣2＝，
由NQ：BC＝AQ：AB，得NQ＝，
再由勾股定理得：PQ＝；
如图1：周长＝2（PA+PQ）＝4+；
如图2：周长＝2（PA+PM）＝12；
如图3：周长＝2（AQ+PQ）＝8+为最长．

故选：D．
二、填空题（本大题共4小题，每小题5分，满分20分）
11．（5分）计算：（）﹣1＝　﹣　．
【分析】直接利用负整数指数幂的定义化简得出答案．
【解答】解：（）﹣1＝（）1＝﹣．
答案为：．
12．（5分）命题“直角三角形两个锐角互余”的条件是　一个直角三角形中的两个锐角　，结论是　这两个锐角互余　．
【分析】命题有条件和结论两部分组成，条件是已知的，结论是结果．
【解答】解：“直角三角形两个锐角互余”的条件是一个直角三角形中的两个锐角，结论是这两个锐角互余．
13．（5分）如图，AB是⊙O的直径，C是弧AB上一点，AP平分∠BAC交⊙O于点P，AB＝3，AC＝1，则点P到线段AB的距离为　　．

【分析】如图，连接BP并延长交AC的延长线于点D，过P作PE⊥AB，垂足为E，根据勾股定理，求得BC、BD，AP的长度；再结合等面积法求PE的长度．
【解答】解：如图，连接BP并延长交AC的延长线于点D，则∠APB＝90°，
∴AP垂直平分BD，则AD＝AB＝3，CD＝2．
连接BC，则∠ACB＝90°，
由勾股定理得：BC＝＝＝2，
再由勾股定理得：BD＝＝＝2，
∴BP＝．
再由勾股定理得：AP＝，
过P作PE⊥AB，垂足为E，
∴PE＝＝．
故答案为：．

14．（5分）在平面直角坐标系中，垂直于x轴的直线l分别与函数y＝﹣x2+4x+5的图象在x轴上方部分和函数y＝﹣x+3的图象交于A、B两点，与x轴交于点C，设点C的坐标为（m，0），若AB＝5BC，则m的值为　2或　．
【分析】根据C的坐标，根据题意表示出A、B的坐标，由AB＝5BC即可得到（﹣m2+4m+5+m﹣3）＝±5（﹣m+3），解得即可．
【解答】解：∵点C的坐标为（m，0），
∴点A（m，﹣m2+4m+5），点B（m，﹣m+3）；
当B点在x轴的上方时，
∵AB＝5BC，
∴（﹣m2+4m+5+m﹣3）＝5（﹣m+3），解得m1＝2，m2＝（舍去）；
当B点在x轴的上方时，
∵AB＝5BC，
∴（﹣m2+4m+5+m﹣3）＝5（m﹣3），解得m1＝，m2＝（舍去）；
故答案为：2或．

三、（本大题共2小题。每小题8分，满分16分）
15．（8分）解方程：．
【分析】分式方程去分母转化为整式方程，求出整式方程的解得到x的值，经检验即可得到分式方程的解．
【解答】解：原方程可以变形为：x+2﹣2x＝﹣1，
解得：x＝3，
经检验x＝3是原分式方程的解．
16．（8分）如图，在边长为1个单位长度的小正方形组成的12×12网格中，给出了格点△ABC（顶点是网格线的交点），并建立平面直角坐标系．
（1）将线段AB绕旋转中心P（3，1）顺时针旋转90°，得到线段A1B1，请在网格内画出线段A1B1；
（2）以原点O为位似中心，将△ABC作位似变换且放大到原来的两倍，得到△A2B2C2，请在网格内画出△A2B2C2．

【分析】（1）分别作出A，B的对应点A1，B1即可．
（2）分别作出A，B，C的对应点A2，B2，C2即可．
【解答】解：（1）如图，线段A1B1即为所求作．
（2）如图，△A2B2C2即为所求作．

四、（本大题共2小题。每小题10分，满分20分）
17．（10分）某书店购进甲、乙两种畅销书共20包花费资金3.45万元，已知甲种书进价为每包0.2万元，其销售利润率为25%；乙种书进价为每包0.15万元，其销售利润率为20%．全部售完后，求该书店共获得的利润．（利润＝售价﹣成本，利润率＝（售价﹣成本）÷成本×100%）
【分析】设该书店购进甲种书x包，则购进乙种书（20﹣x）包，根据总价＝单价×数量，即可得出关于x的一元一次方程，解之即可得出x的值，进而可得出（20﹣x）的值，再利用总利润＝每包的利润×购进数量，即可求出结论．
【解答】解：设该书店购进甲种书x包，则购进乙种书（20﹣x）包，
依题意得：0.2x+0.15（20﹣x）＝3.45，
解得：x＝9，
∴20﹣x＝11，
∴总利润＝0.2×25%×9+0.15×20%×11＝0.78（万元）．
答：全部售完后，求该书店共获得的利润0.78万元．
18．（10分）观察以下等式：第1个等式：100﹣9×11＝1；第2个等式：400﹣18×22＝4；第3个等式：900﹣27×33＝9；第4个等式：1600﹣36×44＝16；第5个等式：2500﹣45×55＝25；按照以上规律，解决下列问题：
（1）写出第6个等式：　3600﹣54×66＝36　；
（2）写出你猜想的第n个等式：　（10n）2﹣9n×11n＝n2．　（用含n用的等式表示），并证明．
【分析】观察、分析题目发现每一个等式的结果是等式序号的平方，等式的第一个数是它序号10倍的平方，第二个数是序号的9倍，依次找出规律，即可得出答案．
【解答】解：（1）由题意可以推导出：第6个等式为：3600﹣54×66＝36；
故答案为：3600﹣54×66＝36．
（2）猜想第n个等式为：（10n）2﹣9n×11n＝n2；
证明：左边＝100n2﹣99n2＝n2＝右边，
所以原等式成立．
故答案为：（10n）2﹣9n×11n＝n2．
五、（本大题共2小题。每小题10分，满分20分）
19．（10分）我国古代数学家刘徽将勾股形（古人称直角三角形为勾股形）分割成一个正方形和两对全等的直角三角形．如图，在△ABC中，∠C＝90°，四边形CDEF为正方形．△ADE≌△AGE，△BGE≌△BFE．已知AB＝10cm，∠BAC＝44°，求正方形CDEF的边长（结果保留位一位小数）．（参考数据：sin44°≈0.69，cos44°≈0.72°，tan44°≈0.97，sin22°≈0.37，cos22°≈0.93，tan22°≈0.40）

【分析】由全等三角形的性质得到EF＝ED＝EG，再由三角函数求出BC，AC，最后根据三角形的面积公式即可求得ED．
【解答】解：∵△ADE≌△AGE，
∴ED＝EG，
∵△BGE≌△BFE，
∴EF＝EG，
∴EF＝ED＝EG，
∵∠C＝90°，AB＝10cm，∠BAC＝44°，cos∠BAC＝，sin∠BAC＝，
∴AC＝10×cos44°≈7.2（cm），
BC＝10×sin44°≈6.9，
∴S△ABC＝（10+7.2+6.9）•ED＝×7.2×6.9，
解得：ED≈2.1（cm），
即正方形CDEF的边长为2.1（cm）．

20．（10分）如图1，在△ABC中，∠C＝90°．
（1）用尺规作图作出斜边AB的中点D（保留作图痕迹，不写作法）；
（2）如图2，过A、C、D三点的⊙O与BC交于点E，若AC＝CE，求∠B的度数．

【分析】（1）作AB的垂直平分线得到AB的中点；
（2）连接AE，CD，先判断△ACE是等腰直角三角形得到∠AEC＝45°，再根据直角三角形斜边上的中线性质得到CD＝BD＝AD，则∠B＝∠BCD，接着根据圆周角定理得到∠ADC＝∠AEC＝45°，然后利用三角形外角性质计算∠B的度数．
【解答】解：（1）如图1，点D为所作；

（2）如图2，连接AE，CD，
∵∠C＝90°，AC＝CE，
∴△ACE是等腰直角三角形，
∴∠AEC＝45°，
∵点D是AB的中点，
∴CD＝BD＝AD，
∴∠B＝∠BCD，
∵∠ADC＝∠AEC＝45°，
∴2∠B＝45°，
∴∠B＝22.5°．
六、（本题满分12分）
21．（12分）九（1）班针对“你最向往的研学目标”的问题对全班学生进行了调查（共提供A、B、C、D四个研学目标，每名学生从中分别选一个目标），并根据调查结果列出统计表绘制扇形统计图．
男、女生最向往的研学目标人数统计表
目标
A
B
C
D
男生（人数）
7
m
2
5
女生（人数）
9
4
2
n
根据以上信息解决下列问题：
（1）m＝　8　，n＝　3　；
（2）扇形统计图中A所对应扇形的圆心角度数为　144°　；
（3）从最向往的研学目标为C的4名学生中随机选取2名学生参加竞标演说，求所选取的2名学生中恰好有一名男生、一名女生的概率．

【分析】（1）先根据C组男女生人数及其所占百分比求出样本容量，再根据B组对应百分比及女生B组人数求解可得m的值，最后根据各组人数之和等于总人数求出n的值；
（2）用360°乘以A组人数所占比例即可；
（3）应用列表法的方法，求出恰好选到1名男生和1名女生的概率是多少即可．
【解答】解：（1）样本容量＝（2+2）÷30%＝40，
依据题意得：（4+m）＝40×30%，
解得：m＝8；
n＝40﹣7﹣8﹣2﹣5﹣9﹣4﹣2＝3；
故答案为：8、3；

（2）（7+9）÷40×360°＝144°；
故答案为：144°．
（3）列表得：

男1
男2
女1
女2
男1
﹣﹣
男2男1
女1男1
女2男1
男2
男1男2
﹣﹣
女1男2
女2男2
女1
男1女1
男2女1
﹣﹣
女2女1
女2
男1女2
男2女2
女1女2
﹣﹣
由表格可知，共有12种等可能的结果数，其中恰好选中1男1女的结果数为8，
所以恰好选中1男1女的概率P＝．
七、（本大题12分）
22．（12分）已知二次函数y＝﹣x2+bx+c和一次函数y＝mx+n的图象都经过点A（﹣3，0），且二次函数y＝﹣x2+bx+c的图象经过点B（0，3），一次函数y＝mx+n的图象经过点C（0，﹣1）．
（1）分别求m、n和b、c的值；
（2）点P是二次函数y＝﹣x2+bx+c的图象上一动点，且点P在x轴上方，写出△ACP的面积S关于点P的横坐标
x的函数表达式，并求S的最大值．
【分析】（1）把直线和曲线经过的点代入得到方程组，求解即可得到答案；
（2）分两种情况：①当点P在y轴左侧时，过点P作PD∥y轴交AC于点D，②当点P在y轴右侧时，过点P作PD∥y轴交AC的延长线于点D，分别根据三角形面积公式得到关系式，利用函数式表示三角形PAC的面积，配方可得答案．
【解答】解：（1）∵二次函数y＝﹣x2+bx+c和一次函数y＝mx+n的图象都经过点A（﹣3，0），一次函数y＝mx+n的图象经过点C（0，﹣1），
∴，
∴，
∵二次函数y＝﹣x2+bx+c和一次函数y＝mx+n的图象都经过点A（﹣3，0），二次函数y＝﹣x2+bx+c的图象经过点B（0，3），
∴，
∴．
（2）由（1）知一次函数与二次函数的解析式分别为：y＝x﹣1或y＝﹣x2﹣2x+3，
①当点P在y轴左侧时，过点P作PD∥y轴交AC于点D，则S△PAC＝×PD×|﹣3|＝PD，

②当点P在y轴右侧时，过点P作PD∥y轴交AC的延长线于点D，

则S△PAC＝×PD×|x+3﹣x|＝PD，
∵点P在抛物线上，设P（x，﹣x2﹣2x+3），则D（x，x﹣1），
∴PD＝﹣x2﹣2x+3x+1＝﹣x2x+4，
∴S△PAC＝PD＝（x2x+4）＝（x+）2+，
即当x＝时，S△PAC最大＝．
八、（本大题14分）
23．（14分）如图1，在矩形ABCD中，AD＝2AB，点P在AD边上，连接BP，过点D作BP的垂线交BP的延长线于点E，连接BD．
（1）连接AE，过点A作AF⊥AE交BE于点F．
①若，求sin∠DBE的值；
②求证：DE＝2BF．
（2）如图2，在BE的延长线上取一点G，连接DG，若∠GDE＝∠ADB，取BG的中点M，连接AM，求证：AM＝（BE﹣GE）．

【分析】（1）①设AB＝a，则AD＝2a，PD＝a，PA＝a，先由勾股定理得PB＝a，BD＝a，再证△PDE∽△PBA，得DE：AB＝PD：PB，则DE＝a，即可求解；
②先由相似三角形的性质得∠PDE＝∠ABF，再证△ABF∽△ADE，得DE：BF＝AD：AB＝2，即可得出结论；
（2）连接AE，过点A作AF⊥AE交BE于点F，先证△DEG∽△DAB，得DE：GE＝AD：AB＝2，则DE＝2GE，得BF＝GE，再证点M是EF的中点，然后由直角三角形斜边上的中线性质即可得出结论．
【解答】（1）①解：设AB＝a，则AD＝2a，PD＝a，PA＝a，
∵四边形ABCD是矩形，
∴∠PAB＝90°，
由勾股定理得：PB＝＝＝a，BD＝＝＝a，
∵DE⊥BP，
∴∠PED＝∠PAB＝90°，
又∵∠DPE＝∠APB，
∴△PDE∽△PBA，
∴DE：AB＝PD：PB，
即＝，
解得：DE＝a，
∴sin∠DBE＝＝＝；
②证明：∵△PDE∽△PAB，
∴∠PDE＝∠ABF，
∵AF⊥AE，
∴∠EAF＝90°，
∴∠DAE+∠PAF＝∠BAF+∠PAF＝90°，
∴∠DAE＝∠BAF，
∴△ABF∽△ADE，
∴DE：BF＝AD：AB＝2，
∴DE＝2BF；
（2）证明：连接AE，过点A作AF⊥AE交BE于点F，如图2所示：
∵∠GDE＝∠ADB，∠DEG＝∠DAB＝90°，
∴△DEG∽△DAB，
∴DE：GE＝AD：AB＝2，
∴DE＝2GE，
由（1）②得：DE＝2BF，
∴BF＝GE，
∵点M是BG的中点，
∴MG＝MB，
∴ME＝MF，
∴点M是EF的中点，
∴AM＝EF＝（BE﹣GE）．